Iterace je opakující se proces, který se přibližuje k určitému cíli. V numerické analýze konstrukcí se tato metoda obvykle používá k nalezení řešení úloh s nelineárními vztahy. Taková úloha se obvykle skládá z rovnice s nelineárními členy, které závisí na proměnné.
Iterační proces začíná v prvním kroku nasazením libovolné počáteční hodnoty pro neznámou proměnnou a vyřešením členů na levé a pravé straně rovnice. Není-li rovnice splněna, proces se opakuje s modifikovanou počáteční hodnotou. Tento iterační postup probíhá tak dlouho, dokud není rovnice splněna. V takovém případě hovoříme o konvergenci a naposledy použitá hodnota proměnné je řešením.
Přesnost tohoto postupu závisí na použitých proměnných. To znamená, že k nalezení přesného řešení musí být obvykle proveden velký počet iterací. Pokud je dostačující řešení s nižší přesností, je konvergence iterace spojena s kritériem tolerance. Nová iterace se spustí pouze tehdy, když je rozdíl mezi členy na levé a pravé straně rovnice větší než definované toleranční kritérium.
Iterační procesy v analýze konstrukcí
- Výpočet vnitřních sil na deformovaném systému (teorie druhého řádu)
- Simulace nelineárních materiálových vlastností (plasticita)
- Zjištění kontaktních napětí mezi dvěma vzájemně spojenými tělesy
Iterace v RFEM a RSTAB
V RFEM 5 a RSTAB 8 jsou kritéria a maximální počet iterací pro nelineární výpočty organizovány pod "Výpočet" → "Parametry výpočtu" v záložce "Globální parametry výpočtu".
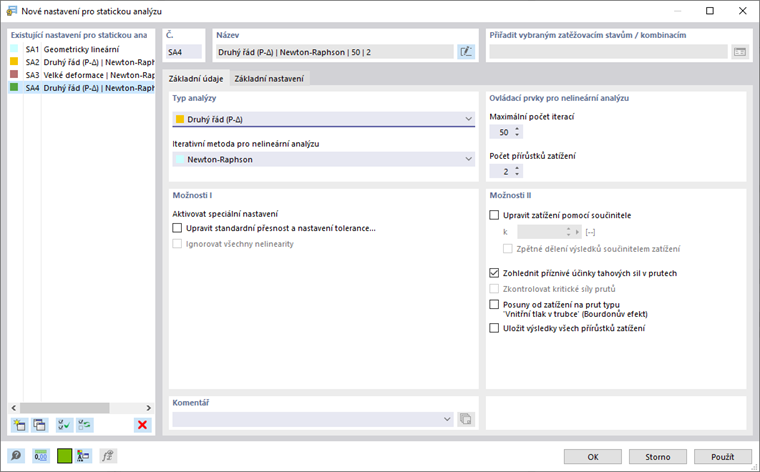
V RFEM 6 a RSTAB 9 jsou parametry pro iterace spravovány v Nastavení statické analýzy.