Une itération est un processus répétitif qui s'approche d'un objectif. Dans l'analyse numérique des structures, cette méthode est généralement utilisée pour trouver une solution à des problèmes avec des relations non linéaires. Ces problèmes consistent généralement en une équation avec des termes non linéaires dépendant d'une variable.
Dans la première étape du processus d'itération, une valeur de départ arbitraire pour la variable inconnue est utilisée, et les termes sur les côtés gauche et droit de l'équation sont résolus. Si l'équation n'est pas satisfaite, le processus se répète avec une valeur de départ modifiée. Ce processus itératif se poursuit jusqu'à ce que l'équation soit satisfaite. Dans ce cas, on parle de convergence, et la dernière valeur de la variable utilisée est la solution.
La précision de cette méthode dépend des variables utilisées. Cela signifie qu'il faut généralement effectuer de nombreuses itérations pour trouver la solution exacte. Si une solution avec une précision réduite est suffisante, la convergence de l'itération est liée à un critère de tolérance. Une nouvelle itération n'est lancée que si la différence entre les termes du côté gauche et du côté droit de l'équation est plus grande qu'un critère de tolérance défini.
Processus itératifs dans l'analyse des structures
- Détermination des efforts internes sur un système déformé (théorie du second ordre)
- Simulation de propriétés matérielles non linéaires (plasticité)
- Détermination des contraintes de contact entre deux corps liés par ajustement
Itérations dans RFEM et RSTAB
Dans RFEM 5 et RSTAB 8, les critères et itérations maximales pour les calculs non linéaires sont organisés sous "Calcul" → "Paramètres de calcul" dans l'onglet "Paramètres de calcul globaux".
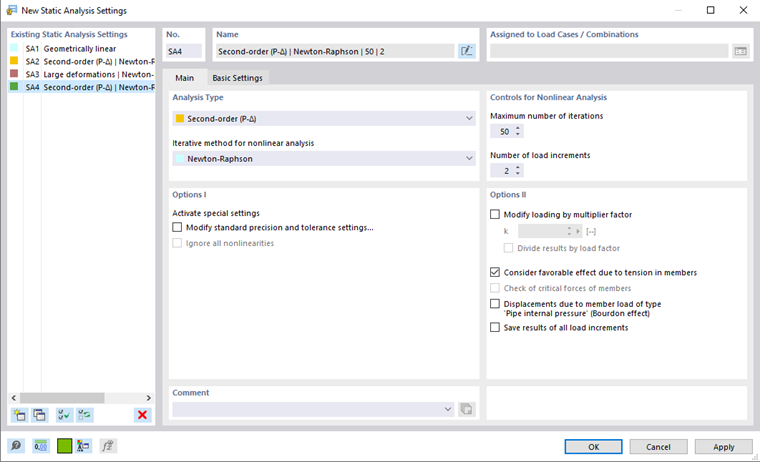
Dans RFEM 6 et RSTAB 9, les paramètres des itérations sont gérés dans les Paramètres d'analyse structurelle.