Iteracja to powtarzalny proces, który zbliża się do celu. W numerycznej analizie konstrukcji metoda ta jest najczęściej wykorzystywana do znajdowania rozwiązań zadań z nieliniowymi zależnościami. Takie zadania zazwyczaj składają się z równania z nieliniowymi wyrazami, które zależą od jednej zmiennej.
Proces iteracyjny rozpoczyna się od wstawienia dowolnej wartości początkowej dla nieznanej zmiennej i rozwiązuje wyrazy po lewej i prawej stronie równania. Jeśli równanie nie jest spełnione, proces powtarza się z zmodyfikowaną wartością początkową. Ten iteracyjny proces trwa, aż równanie zostanie spełnione. W tym przypadku mówi się o zbieżności, a wartość zmiennej w ostatniej iteracji jest rozwiązaniem.
Dokładność tej metody zależy od wprowadzonych zmiennych. Oznacza to, że do znalezienia dokładnego rozwiązania często potrzeba bardzo wielu iteracji. Jeśli rozwiązanie o zmniejszonej dokładności jest wystarczające, zbieżność iteracji wiąże się z kryterium tolerancji. Nowa iteracja jest inicjowana tylko wtedy, gdy różnica między wyrazami po lewej i prawej stronie równania jest większa niż zdefiniowane kryterium tolerancji.
Procesy iteracyjne w analizie konstrukcji
- Wyznaczanie sił wewnętrznych w odkształconym systemie (Teoria drugiego rzędu)
- Symulacja nieliniowych właściwości materiałowych (Plastyczność)
- Wyznaczanie naprężeń kontaktowych między dwoma ciałami połączonymi na zasadzie formy
Iteracje w RFEM i RSTAB
W RFEM 5 i RSTAB 8 kryteria i maksymalne iteracje obliczeń nieliniowych są zorganizowane w "Obliczenia" → "Parametry obliczeń" w zakładce "Globalne parametry obliczeń".
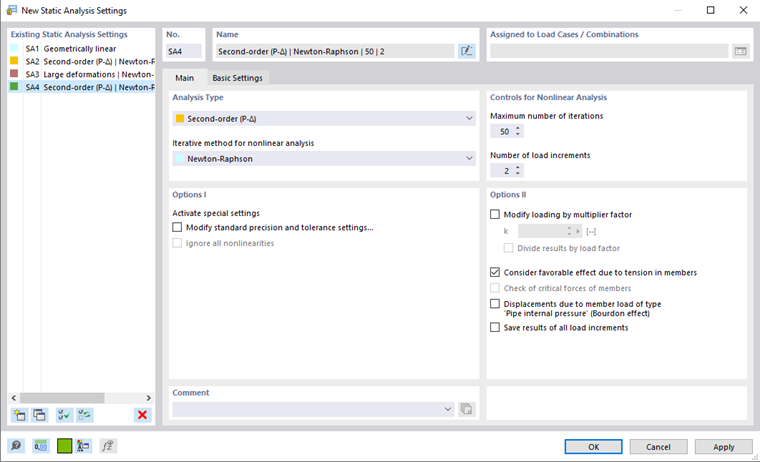
W RFEM 6 i RSTAB 9 parametry iteracji są zarządzane w Ustawienia analizy statycznej.