Una iterazione è un processo ripetitivo che si avvicina a un obiettivo. Nell'analisi strutturale numerica, questo metodo viene generalmente utilizzato per trovare una soluzione a problemi con relazioni non lineari. Tali problemi consistono solitamente in un'equazione con termini non lineari che dipendono da una variabile.
Il processo di iterazione inizia inserendo un valore iniziale arbitrario per la variabile sconosciuta e risolvendo i termini sul lato sinistro e destro dell'equazione. Se l'equazione non è soddisfatta, il processo si ripete con un valore iniziale modificato. Questo procedimento iterativo continua fino a quando l'equazione è soddisfatta. In tal caso, si parla di convergenza e il valore della variabile utilizzato per ultimo è la soluzione.
La precisione di questo metodo dipende dalle variabili utilizzate. Ciò significa che per trovare la soluzione esatta, spesso sono necessarie molte iterazioni. Se una soluzione con precisione ridotta è sufficiente, la convergenza dell'iterazione è legata a un criterio di tolleranza. In questo caso, una nuova iterazione viene avviata solo quando la differenza tra i termini del lato sinistro e destro dell'equazione è maggiore di un criterio di tolleranza definito.
Processi iterativi nell'analisi strutturale
- Determinazione delle azioni interne sul sistema deformato (Teoria del II ordine)
- Simulazione di proprietà dei materiali non lineari (plasticità)
- Determinazione delle tensioni di contatto tra due corpi collegati a forma
Iterazioni in RFEM e RSTAB
In RFEM 5 e RSTAB 8, i criteri e le iterazioni massime per i calcoli non lineari sono organizzati sotto "Calcolo" → "Parametri di calcolo" nella scheda "Parametri di calcolo globali".
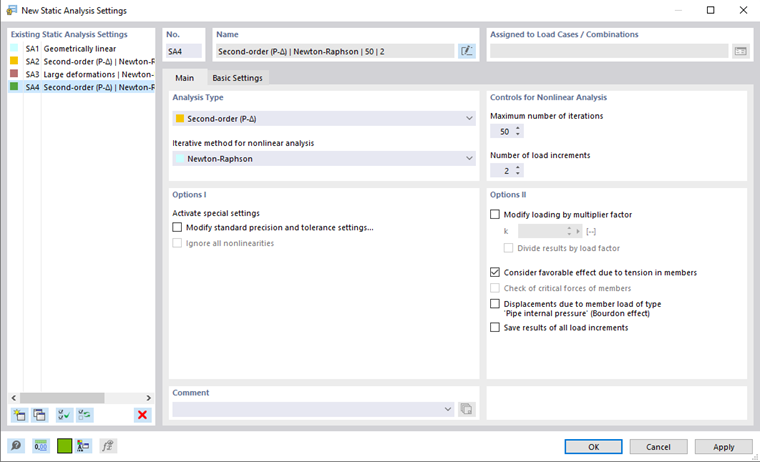
In RFEM 6 e RSTAB 9, i parametri per le iterazioni sono gestiti nelle Impostazioni dell'analisi statica.