En raison de la manière dont cette structure est conçue, il n'est pas possible de supposer un maintien latéral et torsionnel lors de la détermination du moment critique élastique idéal pendant l'analyse de stabilité. Il réduirait en effet la résistance de la structure et doit donc être considéré. En revanche, l'effet ultime de la capacité de charge du maintien en rotation des tôles trapézoïdales est pris en compte.
Le modèle de cet article technique est basé sur l'exemple 1.3 Panne dans la littérature technique [1]. Les pannes sont des poutres à travée simple entre les fermes et ont une longueur de 9,0 m et une inclinaison de 3,18°.
Chargement et efforts internes
Les tôles trapézoïdales continues reposent sur un total de cinq pannes avec une largeur d’application d’environ 4,50 m. Selon les tableaux pertinents de la littérature technique pour les poutres continues, le facteur de charge d'appui B est de 1,143. Les valeurs caractéristiques des charges surfaciques pour le poids propre, la neige et le vent sont données dans {%}#Refer [1]]]. L'entrée ou le calcul des charges de barre résultantes est effectué à l'aide du paramétrage disponible dans RFEM et RSTAB.
La combinatoire automatique dans RFEM/RSTAB est effectuée uniquement pour l'état limite ultime selon l'Équation 6.10 de l'EN 1990. Les combinaisons de charges générées résultent des efforts internes de calcul suivants.
Calcul du moment critique élastique idéal et analyse de stabilité
Pour déterminer Mcr selon la méthode des valeurs propres, un modèle de barre interne avec quatre degrés de liberté est créé dans le module additionnel RF-/STEEL EC3. Comme il n'est pas possible de supposer un maintien latéral et torsionnel en dehors des panneaux de contreventement en raison de la formation sans raidisseur, le maintien en rotation résultant de la déformation de la section de la panne doit être calculé. Cette opération est effectuée selon [5] comme suit.
où :
Une méthode beaucoup plus complexe peut être trouvée dans [6].
De plus, on considère la capacité de charge ultime de la tôle trapézoïdale (135/310-0,88 en position positive). Le maintien en rotation effectif CD est calculé automatiquement dans RF-/STEEL EC3 selon l'Équation E.11 [3] si vous entrez les données correspondantes dans les tableaux d'entrée 1.12 et 1.13.
où :
Avec ces valeurs, vous avez la possibilité d'effectuer l'analyse de stabilité selon la méthode analytique décrite dans {%}#Refer [2]]], section 6.3. En raison de la faible inclinaison de la toiture, le composant en direction de l'axe faible peut être négligé. Ainsi, il serait possible d'effectuer un calcul selon la Section 6.3.3 « Barres uniformes fléchies et comprimées » ou selon la Section 6.3.4 « Méthode générale de vérification du flambement latéral et du déversement de composants structuraux ».
La méthode selon la Section 6.3.4 est sélectionnée car l'entrée des conditions d'appui est plus simple dans ce cas. Si le moment autour de l'axe faible ne peut plus être négligé, nous devons sélectionner la méthode selon la Section 6.3.3.
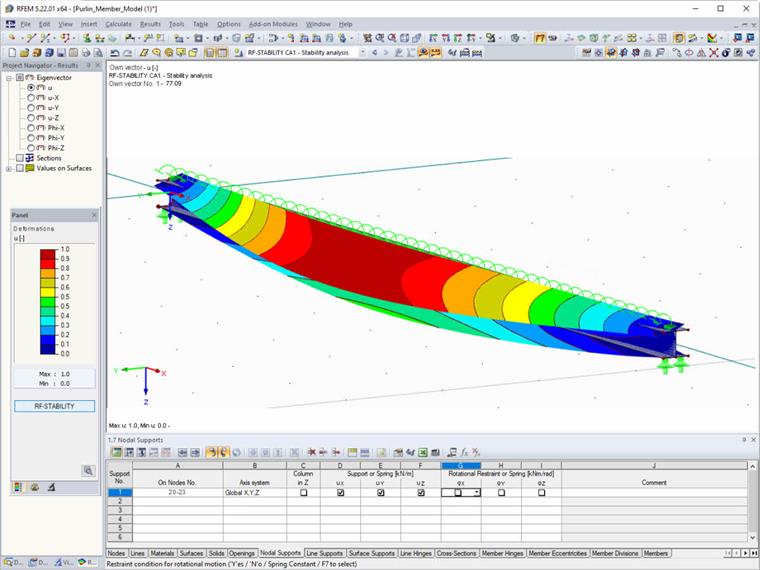
La figure suivante affiche les entrées requises des appuis nodaux pour la méthode des valeurs propres (modèle de barre interne avec quatre degrés de liberté).
La capacité portante de la panne peut être vérifiée à l'aide de la méthode générale. Le facteur de charge critique pour la CO 3 et le système défini sont de 2,535. Vous pouvez également afficher graphiquement le mode propre correspondant.
Le moment critique élastique idéal est ainsi calculé comme suit :
Calcul du moment critique élastique idéal sur le modèle surfacique
Un modèle surfacique est utilisé pour valider le moment critique élastique idéal Mcr. Vous pouvez créer ce type de modèle dans RFEM en quelques clics grâce à la fonction « Générer des surfaces à partir d'une barre ». Avec le module additionnel RF-STABILITY, un facteur de charge critique de 2,55 est calculé pour la combinaison de charges déterminante 3, ce qui permet d'obtenir :
Base de connaissance