验算示例
德儒巴结构分析软件的力学计算功能全面, 并且容易理解和掌握。 这里的验算示例可以帮助您理解软件的工作原理和计算方法。
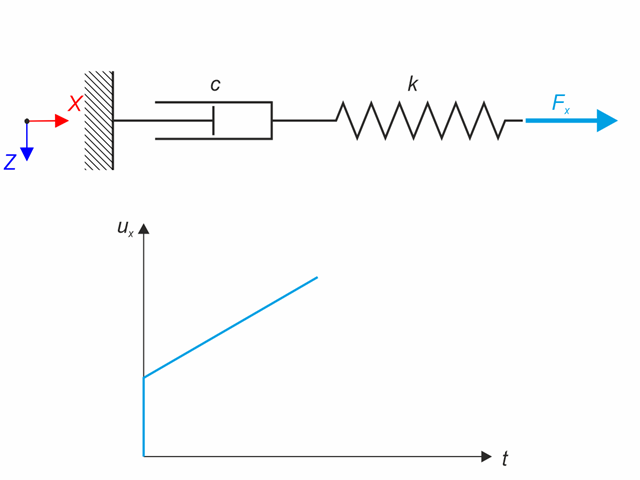
Maxwell 材料模型由串联的线性弹簧和粘滞阻尼器组成。 在该验算示例中,对模型的时特性进行了测试。 Maxwell 材料模型受恒力 Fx加载。 该力在初始弹簧力的作用下,在阻尼器的作用下变形不断扩大。 观察加载时(20 秒)和分析结束时(120 秒)的变形。 使用“线性隐式 Newmark 方法”进行时程分析。
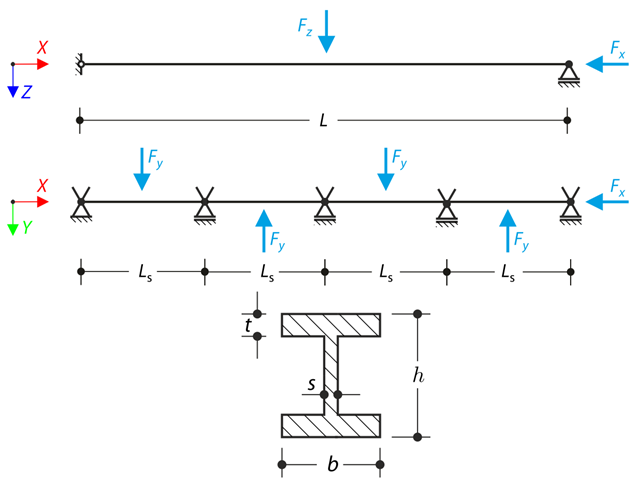
施加轴力和弯矩(缺陷替换)加载四跨连续梁。 所有支座都是叉形的,自由翘曲。 计算位移uy和uz ,弯矩My 、Mz 、Mω和MTpri ,以及转角φx 。 验算示例是基于 Gensichen 和 Lumpe 介绍的示例.
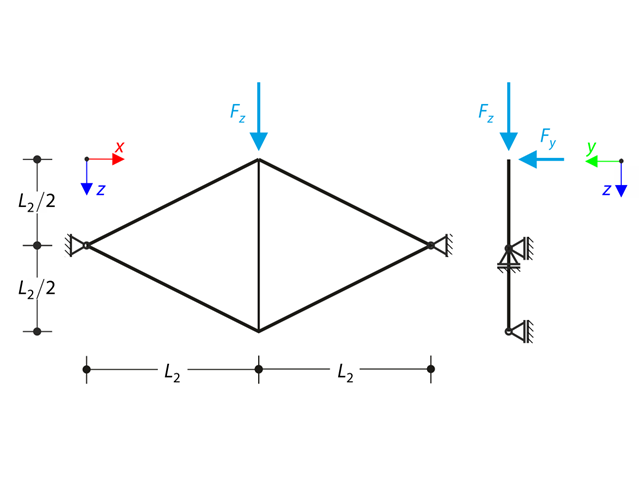
在该示例中将有效长度和临界荷载系数与手动计算进行了比较,本教程将在 RFEM 6 中使用“结构稳定性”模块进行计算。 结构体系是在刚架结构上加两根铰接柱。 该柱子承受竖向集中荷载。
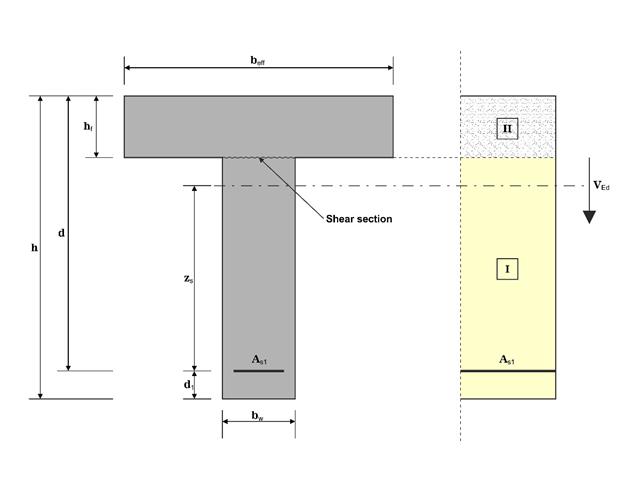
在本例中,不同时间浇筑的混凝土与相应钢筋之间界面的剪力按照 DIN EN 1992-1-1 确定。 下面将使用 RFEM 6 获得的结果与手算结果进行比较。
本例题中的钢筋混凝土梁为两跨悬臂梁。 截面沿悬臂长度方向不断变化(变截面)。 计算最终极限状态下的内力以及所需的纵向和剪切钢筋。
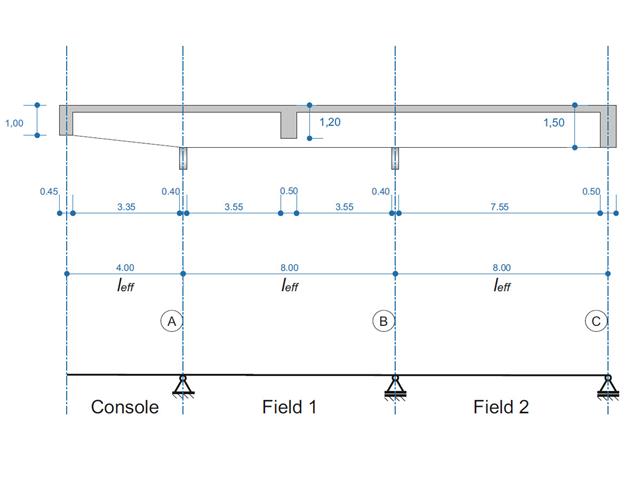
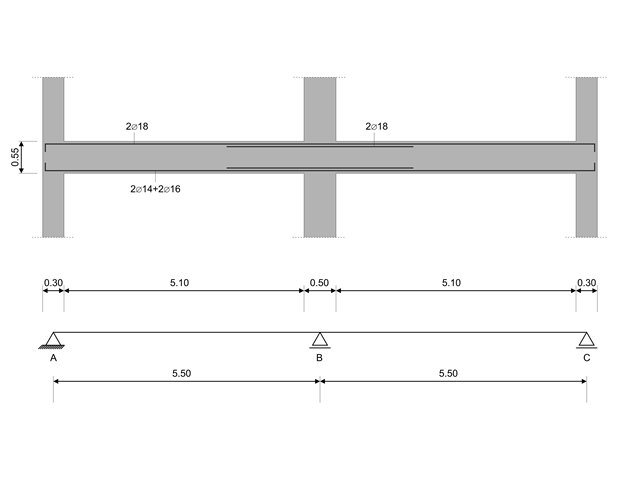
在该验算示例中,梁的剪力承载力设计值按照规范 EN 1998-1 中 5.4.2.2 和 5.5.2.1 以及柱受弯承载力设计值按照 5.2.3.3(2 ). 该梁由一个跨度为 5.50 米的两跨钢筋混凝土梁组成。 梁是框架的一部分。 将得到的结果与 {%于#Refer [1]]] 中的结果进行比较。
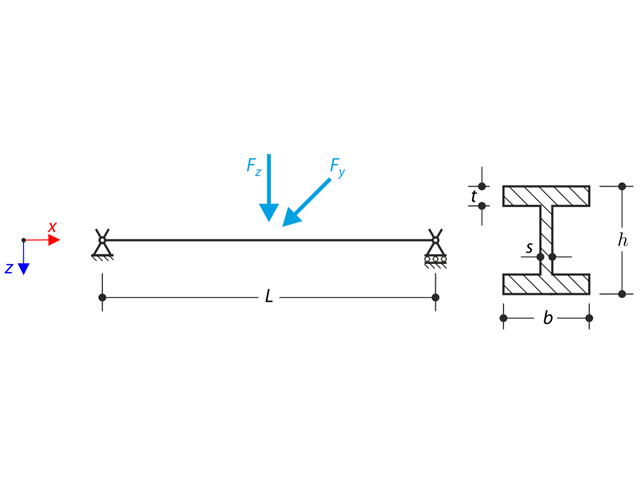
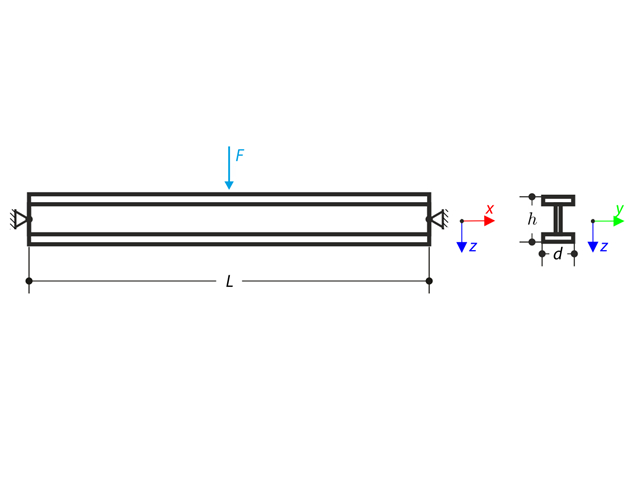
两端的铰支座限制 I 型钢的轴向转动(翘曲不被限制)。 两个横向力在中间施加。 示例中忽略自重。 计算结构的最大挠度 uy,max和 uz,max ,最大转角 φx,max ,最大弯矩 My,max和 Mz,max以及最大扭矩 MT,max, MTpri,max , MTsec,max与 Mω,max 验算示例是基于 Gensichen 和 Lumpe 介绍的示例.
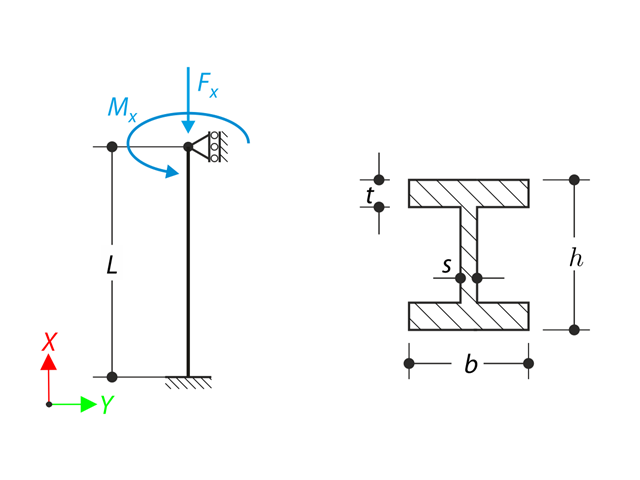
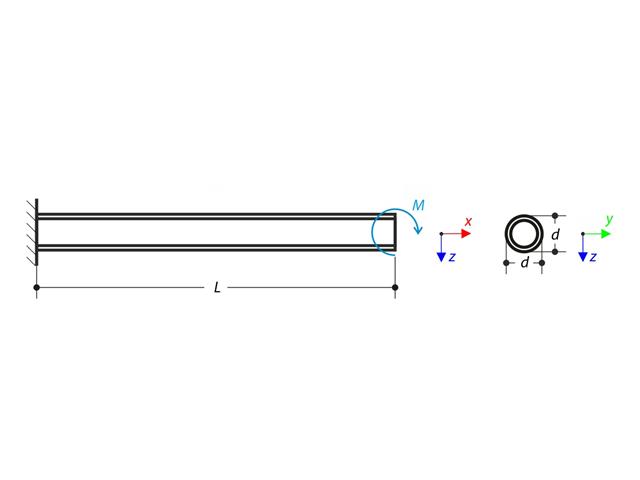
在给定的边界条件下,杆件受到扭矩和轴力。 忽略其自重,计算梁的最大扭转变形和内部扭矩,定义为主扭矩和由轴力产生的扭矩之和。 在假设或忽略轴力的影响时,提供这些值的比较。 验算示例是基于 Gensichen 和 Lumpe 介绍的示例.
一个 QRO 型材的薄壁悬臂梁,左端完全固定并且无翘曲现象。 悬臂梁承受扭矩。 该模型考虑了小变形,并忽略了自重。 计算最大转角,主要弯矩,次要弯矩和翘曲弯矩。 验算示例是基于 Gensichen 和 Lumpe 介绍的示例.
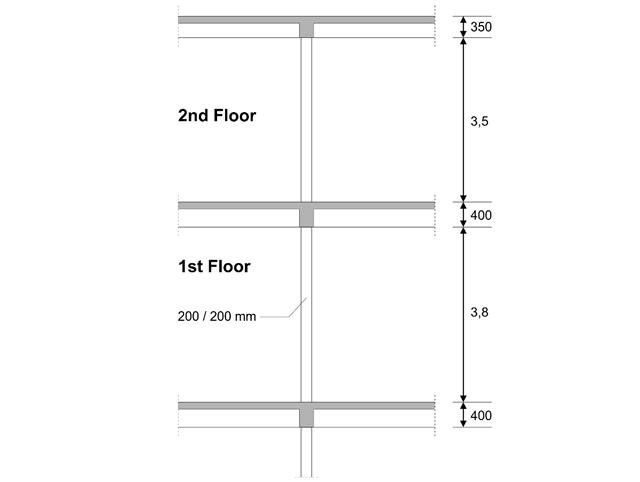
设计一个三层建筑的内柱。 柱子与上、下梁采用整体连接。 然后与 EC2-1-2 中柱的抗火设计[#Refer [1]]] 进行了验证,结果与 [1] 进行了比较。
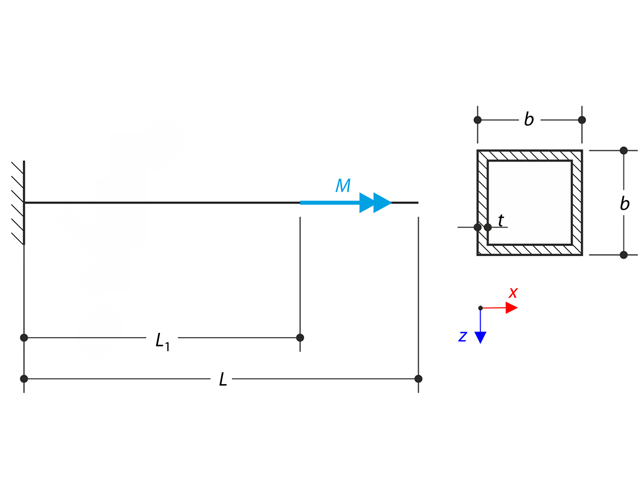
该梁左完全固定(约束翘曲),右末端由叉形支座支承(自由翘曲)。 梁受到扭矩,纵向力和横向力的作用。 计算主扭矩、次扭矩和翘曲弯矩的属性。 验算的例子是基于 Gensichen 和 Lumpe 介绍的例子(见参考资料)。
左端支承着一个工字形的悬臂梁,给悬臂梁施加扭矩 M。 本例的目的是对固定式支座和货叉式支座进行比较,并研究一些有代表性的问题的行为。 并与通过板的解决方案进行了比较。 验算示例是基于 Gensichen 和 Lumpe 介绍的示例.
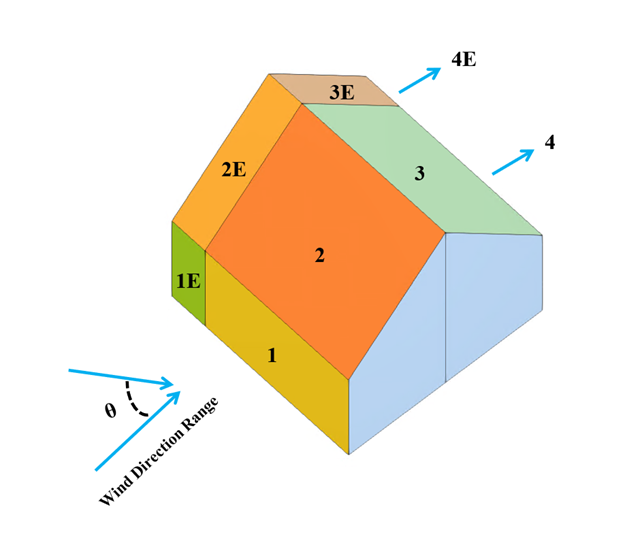
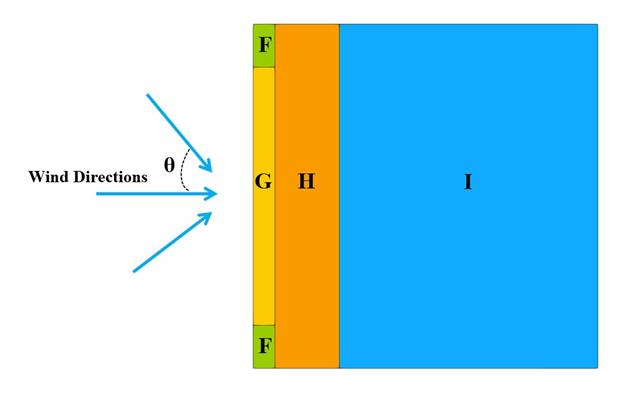
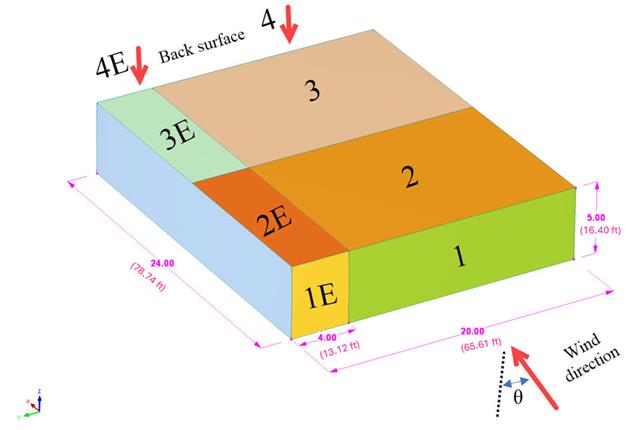
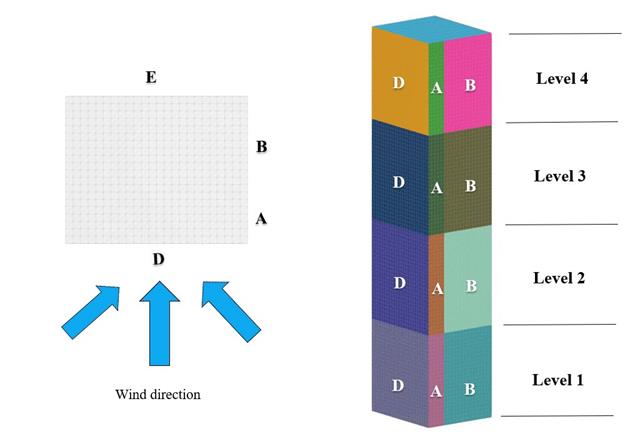
在当前的验证示例中,我们按照 EN 1991-1-4 平屋面示例研究一般结构设计 (Cp,10 ) 和局部结构设计例如幕墙或幕墙结构设计 (Cp,1 ) 的风压值 { %!#Refer [1]]] 并 日本风洞数据库 . 关于带尖屋檐的三维屋面的推荐设置将在下一部分中介绍。
在当前的验证示例中,我们使用 ASCE7-22 [1] 研究平屋面和墙体的风压系数 (Cp)。 在章节 28.3(风荷载 - 主要抗风荷载体系)和图 28.3-1(荷载工况 1)中有一个表格,其中显示了不同屋面倾角下的 Cp 值。
该模型基于 [1] 的示例 4: 点支座楼板。
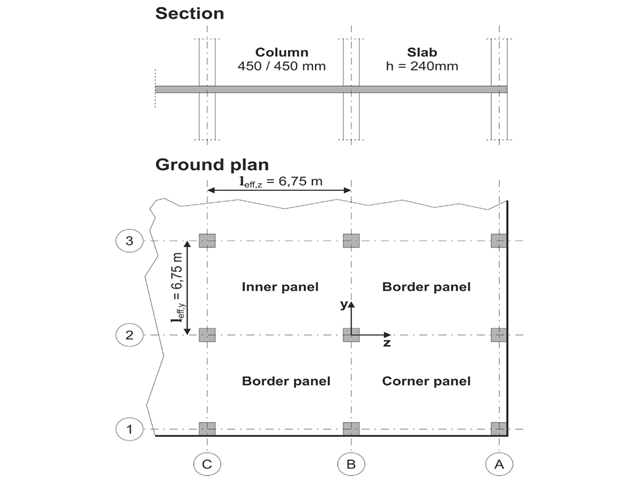
将设计一栋办公楼的平板,该建筑采用对裂缝敏感的轻质墙体。 内部、边缘和角部板件将被检查。 柱子和平板是整体连接的。 边柱和角柱与板的边缘齐平。 柱的轴线形成一个方形网格。 它是一个刚性体系(用剪力墙加劲的建筑物)。
该办公楼有5层,层高3.000 m。 假设的环境条件定义为“封闭的内部空间”。 主要是静力作用。
本例的重点是确定板在满载情况下的弯矩和柱上方所需的配筋。
该模型基于 [1] 的示例 4: 点支座楼板。 内力和所需的纵向配筋参见验证示例 1022。 在本例中,我们在轴 B/2 上检查冲切。
日本建筑学会 (AIJ) 介绍了许多著名的风洞模拟基准场景。
下面的文章将围绕“案例E - 新泻市低层建筑密集的实际城区中的建筑群”展开。
下面将在 RWIND2 中对所描述的场景进行模拟,并将结果与 AIJ 的模拟结果和实验结果进行比较。
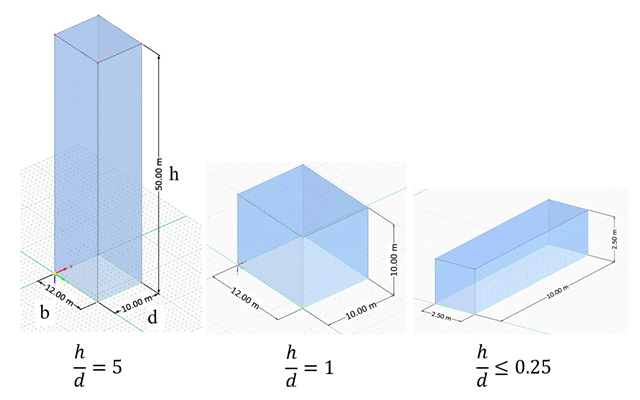
在当前的验证示例中,我们按照欧洲规范 EN 1991-1-4 研究了矩形建筑的一般结构设计 (Cp,10 ) 以及幕墙或外墙设计 (Cp,1 ) 的风压值[1]. 如果是三维情况,我们将在下一部分中详细介绍。
Das eine Reihe an bekannten Benchmark-Szenarien für Windsimulation vorgestellt。
Der Nachfolgende Beitrag dreht sich dabei um den “案例 A - 高层建筑,形状为 2:1:1”。
Im Folgenden wird das beschriebene Szenario in RWIND2 nachgebildet und die Ergebnisse mit den simulierten und derexperimentellen Resultate des AIJ verglichen.
日本建筑学会 (AIJ) 介绍了许多著名的风洞模拟基准场景。
下面的文章介绍的是“案例 D - 城市街区之间的高层建筑”。
下面将在 RWIND2 中对所描述的场景进行模拟,并将结果与 AIJ 的模拟结果和实验结果进行比较。
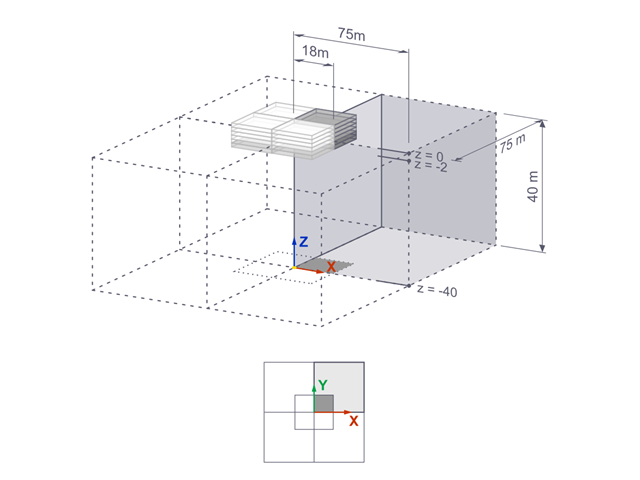
使用 RFEM 计算了湖相黏土上刚性方形地基[1]的沉降。 已对四分之一的基础进行建模。 基础两侧的宽度为 75.0 m。 施工阶段用于生成结果。
在当前的验证示例中,我们按照 EN 1991-1-4 [1] 研究了立方体形状的风力系数 (Cf )。 如果是三维情况,我们将在下一部分中详细介绍。
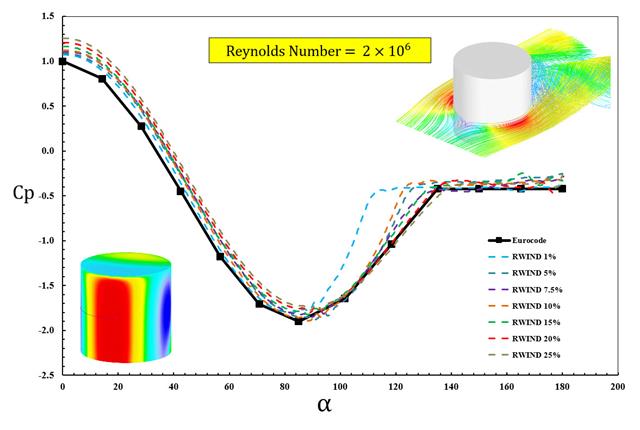
EN 1991-1-4 [1]、ASCE/SEI 7-16 和 NBC 2015 等现有标准给出了风荷载参数,例如风压系数 (Cp )基本形状。 重要的是如何更快,更准确地计算风荷载参数,而不是使用标准中的耗时且有时复杂的公式。
对于图 1 所示弯矩框架中的 ASTM A992 材料柱,在最大重力荷载作用组合下,使用荷载设计法 LRFD 和 ASD 计算所需的强度和有效长度系数。