Norma EN 1991-1-4 uvádí pro daný případ koncepci výpočtu s aerodynamickými a redukčními součiniteli. Na základě těchto údajů se určí výsledná síla větru působící na konstrukční prvek. Rozdělení tlaku větru na dílec se zde neuvádí. Síla větru se tak určí z následujícího vztahu:
|
cscd |
dvousložkový součinitel konstrukce pro zohlednění účinku zatížení větrem, kdy maximální tlaky větru nepůsobí současně na celý povrch konstrukce (cs), společně s účinkem kmitání konstrukce, vyvolaného turbulencí (cd) |
|
cf |
součinitel síly pro stavební objekt nebo jeho část |
|
qp(ze) |
maximální dynamický tlak větru v referenční výšce ze |
|
Aref |
referenční plocha stavebního objektu nebo jeho části |
Pokud budeme předpokládat, že posuzovaný konstrukční prvek je tuhé nepoddajné těleso, na které působí konstantní proudění vzduchu, pak se výpočet síly větru zjednoduší následujícím způsobem:
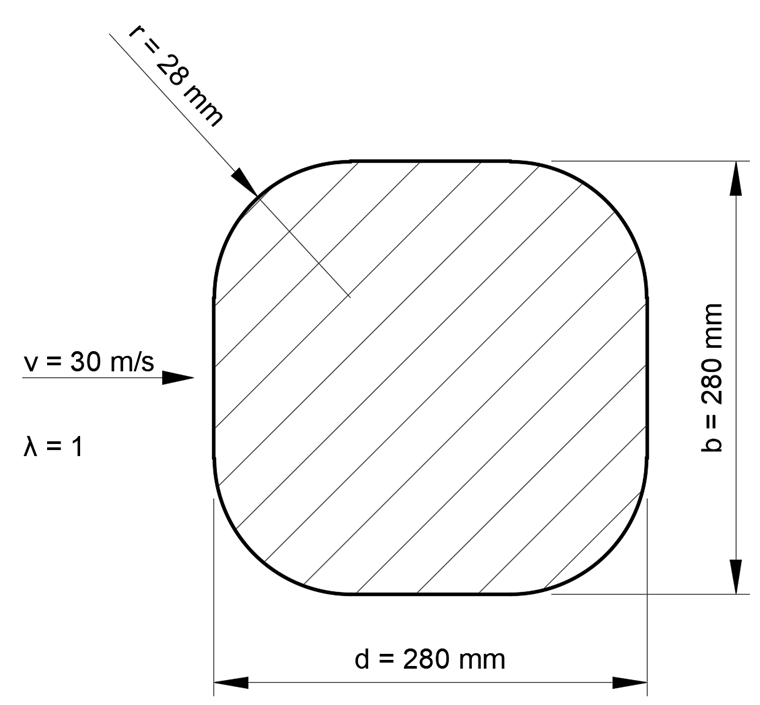
U neštíhlého konstrukčního prvku s kvadraticky zaobleným průřezem se součinitel síly cf stanoví podle [1] následovně:
|
cf,0 |
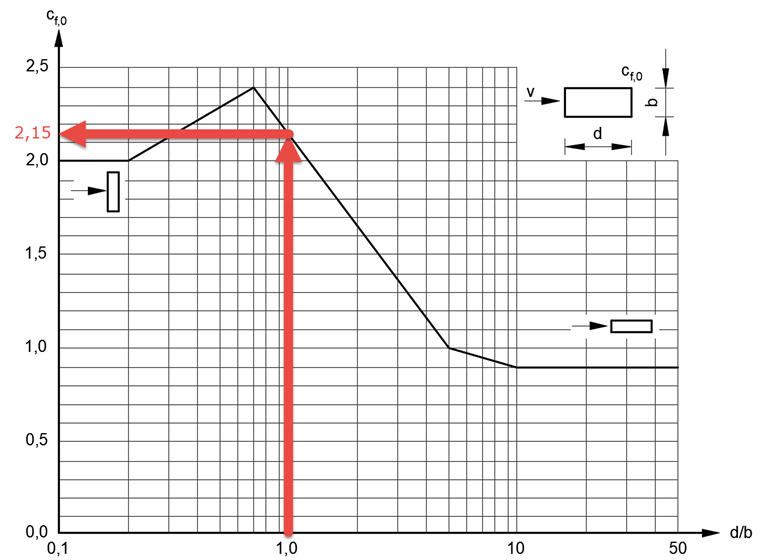
součinitel síly pro průřezy s ostrými rohy |
|
Ψr |
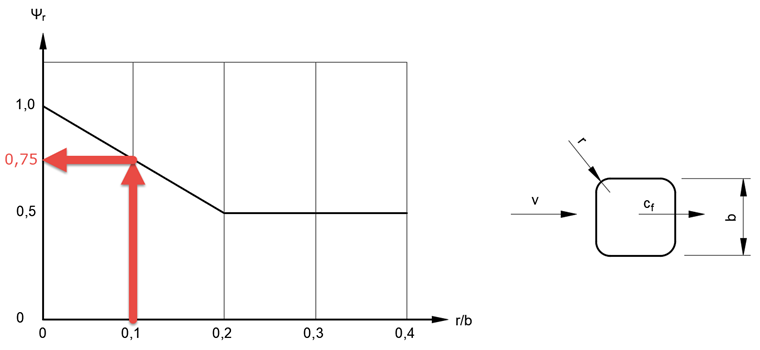
redukční součinitel pro čtvercové průřezy se zaoblenými rohy |
|
Ψλ |
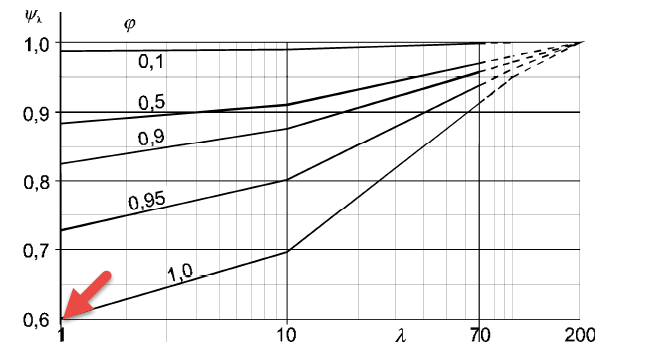
redukční součinitel pro zohlednění efektivní štíhlosti λ v závislosti na součiniteli plnosti φ |
|
φ |
je poměr plnosti pro zohlednění propustnosti návětrných ploch |
Běžný výpočet zatížení větrem
Exemplarisch ergibt sich nach [1] für diese Bauteileigenschaften
součinitel síly cf = 0,97.
Tato hodnota vychází ze součinitele síly cf, 0 = 2,15 v závislosti na poměru délky stran d/b = 280 mm/280 mm = 1,
dále redukčního součinitele Ψr = 0,75 v závislosti na poměru poloměru zaoblení a délky stran r/b = 28 mm/280 mm = 0,1
a nakonec redukčního součinitele Ψλ = 0,6 v závislosti na štíhlosti λ = 1 za předpokladu plně uzavřeného povrchu dílce φ = 1.
Dynamický tlak q = 563 N/m² působící na referenční plochu Aref = 280 mm ⋅ 280 mm = 0,0784 m² se stanoví ze vztahu:
Ve výsledku tak působí síla větru Fw = 0,97 ⋅ 563 N/m² ⋅ 0,0784 m² = 43 N na konstrukční prvek ve směru větru.
Numerická metoda stanovení zatížení větrem
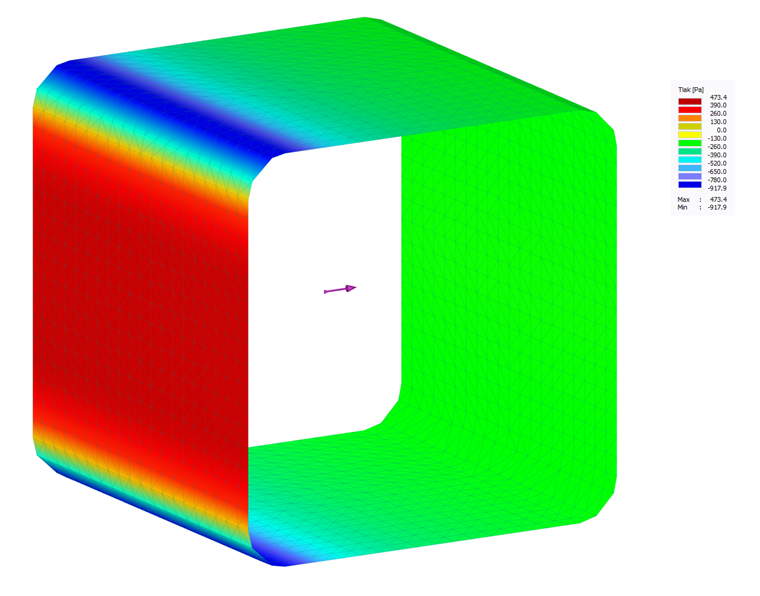
Pokud kromě síly větru Fw potřebujeme stanovit také rozdělení tlaku větru na daný konstrukční prvek, lze příslušné rozdělení tlaku stanovit například analýzou CFD. V takovém případě se dílec fiktivně umístí do numerického větrného tunelu a v závislosti na výsledném rozdělení tlaku a rychlosti okolo dílce se stanoví rozdělení tlaku na daný dílec.
Program RWIND Simulation umožňuje takovou numerickou simulaci proudění vzduchu okolo budov a jiných objektů na základě 3D sítě konečných objemů. Tuto síť program generuje automaticky a velikost konečných objemů uzpůsobuje modelu ve vzájemné korelaci. Čím blíže povrchu modelu jsou konečné objemové prvky, tím je generovaná síť jemnější. Pro tento proces používá program generátor sítě OpenFOAM (SnappyHexMesh). Pro výpočet proudění vzduchu a stanovení tlaku větru na povrchu modelu se používá stabilní řešič SimpleFOAM pro nestlačitelné turbulentní proudění.
Für das gegebene Beispiel ergibt eine RWIND-Simulation-Berechnung eine ähnliche Windkraft Fw = 41 N. Neben dieser Resultierenden gibt das Programm auch die Druck- und Windgeschwindigkeitsverteilung um das Bauteil sowie die Druckverteilung auf dem Bauteil mit aus.