System
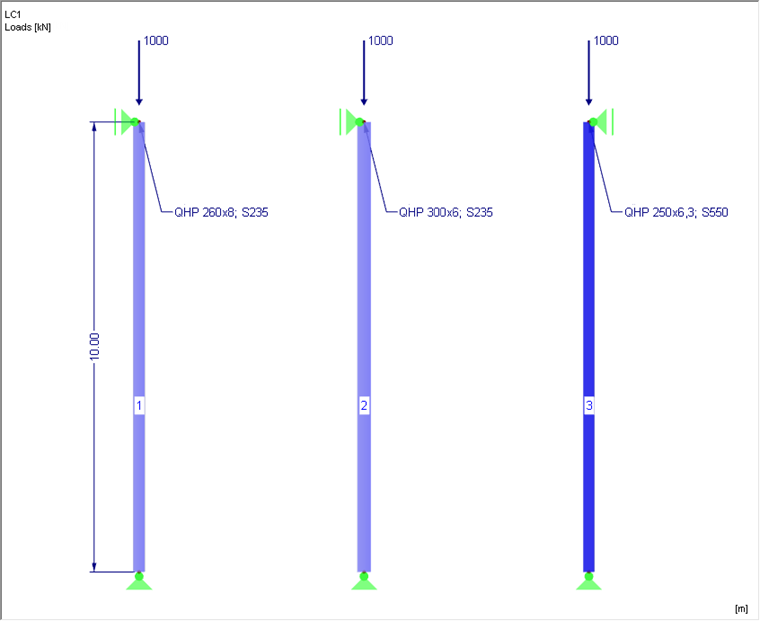
The column cross-section is a hollow square section. The structural system and the design load are shown in Image 01.
Design
The steel columns displayed in Image 1 are subjected to specific loads, and their flexural buckling will be analyzed. Since there is axial compression in the current case, the design can be carried out according to EN 1993‑1‑1, Clause 6.3.1. The design according to the second-order analysis with precamber would be an option as well.
The aim is to come to a conclusion in terms of efficiency and to examine the application of higher steel strengths.
The following table shows the corresponding designs with manual calculation.
| Section | QHP 260x8 | QHP 300x6 | QHP 250x6.3 |
| Material | S 235 | S 235 | S 550 |
| Classification | |||
|---|---|---|---|
| c/t | 28.5 | 46 | 35.68 |
| Cross-Section Area [cm²] | 79.95 | 70.17 | 60.99 |
| Stress [kN/cm²] | -12.51 | -14.25 | -16.40 |
| Stress ratio | 1.0 | 1.0 | 1.0 |
| Material factor | 1.0 | 1.0 | 0.65 |
| Max c/t for Class 1 | 33 | 33 | 21.57 |
| Max c/t for Class 2 | 38 | 38 | 24.84 |
| Max c/t for Class 3 | 42 | 42 | 27.45 |
| Cross-Section Class | 1 | 4 | 4 |
| Effective Section Properties | |||
| 0.81 | 0.97 | ||
| 0.89 | 0.8 | ||
| beff = ρ ∙ b [cm] | 24.81 | 17.98 | |
| A or Aeff [cm²] | 79.95 | 63.51 | 49.79 |
| Flexural Buckling Design | |||
| [kN] | 1,745.66 | 2,089.14 | 1,246.46 |
| Npl = A ∙ fy or Aeff ∙ fy [kN] | 1,878.83 | 1,492.49 | 2,738.45 |
| 1.04 | 0.85 | 1.48 | |
| Imperfection Factor α | 0.21 (BC a) | 0.21 (BC a) | 0.13 (BC a0) |
| Φ = 0.5 ∙ [1 + α (λ - 0.2) + λ²] | 1.13 | 0.93 | 1.68 |
| 0.639 | 0.769 | 0.404 | |
| [kN] | 1,091.4 | 1,043.4 | 1,005.8 |
| 0.92 | 0.96 | 0.99 | |
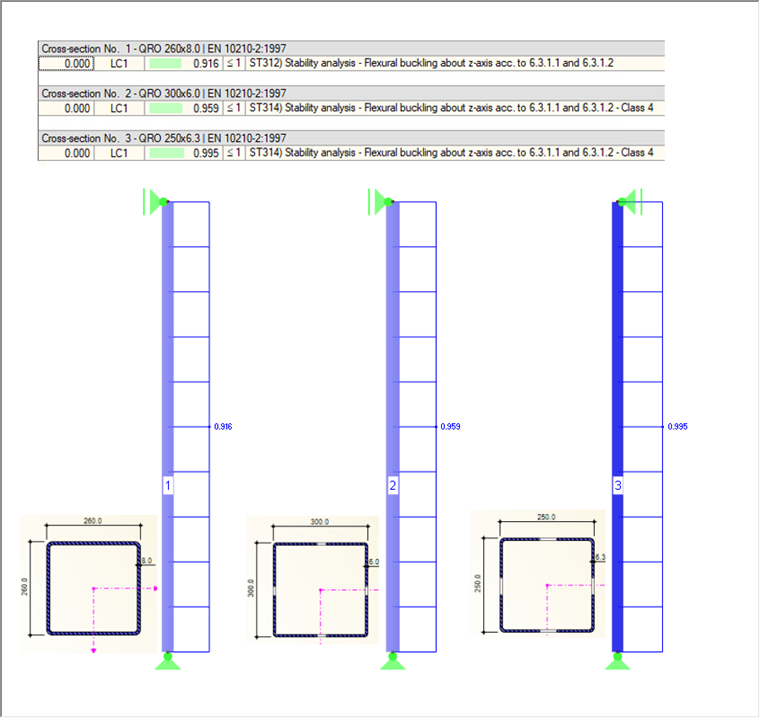
All three columns are capable of bearing the specified load. The middle column has larger external dimensions, but is slender with regard to the cross‑section dimensions. The cross-section is, therefore, classified in cross-section class 4, and the design has to be carried out with the effective cross-section area according to EN 1993-1-5. It results in a reduction of 11 % due to local buckling. However, the larger external dimensions have a positive effect on the critical load Ncr. As a result, this column has a more favorable slenderness ratio for flexural buckling.
In the case of the middle column (member 2), about 12% of the cross‑sectional area can be saved compared to the left column which has the same steel grade.
In the case of the right column (member 3), about 13 % of the cross‑sectional area can still be reduced compared to the middle column. The smaller dimensions have a negative effect on the critical load. About 20% of the cross‑sectional area is also ineffective due to the local buckling. The slenderness ratio of this column is significantly worse than in the case of the other columns, although calculating Ncr with the real cross-section area is allowed. However, the design is fulfilled due to the larger yield strength.
The design results with RF-/STEEL EC3 are shown in Figure 02.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
