System
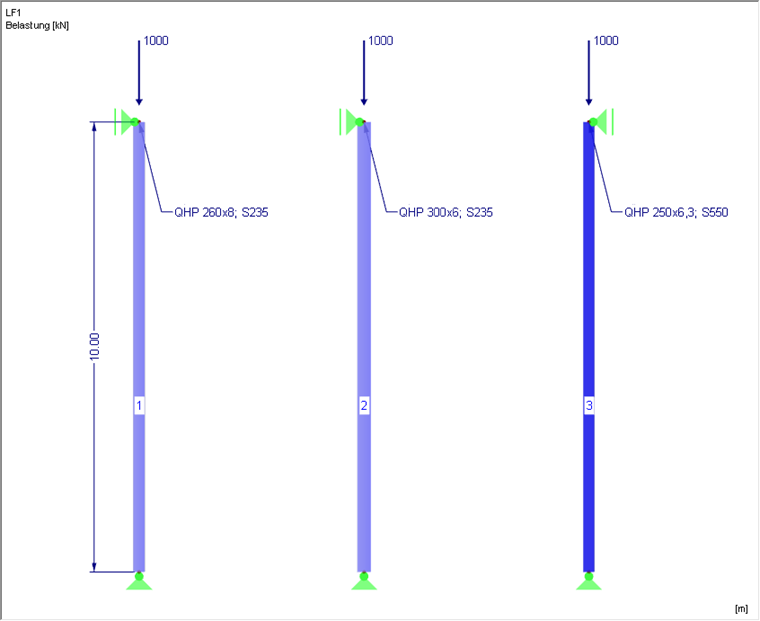
Bei dem Stützenquerschnitt handelt es sich um ein quadratisches Hohlprofil. Das statische System sowie die Bemessungslast sind in Bild 01 dargestellt.
Bemessung
Die abgebildeten Stahlstützen sollen unter der angegebenen Belastung gegen Biegeknicken untersucht werden. Da in diesem Fall planmäßig mittiger Druck vorliegt, kann die Bemessung nach EN 1993-1-1 Abs. 6.3.1 durchgeführt werden. Alternativ wäre ein Nachweis nach Theorie II. Ordnung mit Vorkrümmung denkbar.
Es sollen zudem Schlussfolgerungen hinsichtlich der Wirtschaftlichkeit getroffen beziehungsweise der Einsatz höherer Stahlfestigkeiten untersucht werden.
In folgender Tabelle finden sich die entsprechenden Nachweise in Handrechnung.
| Querschnitt | QHP 260x8 | QHP 300x6 | QHP 250x6,3 |
| Material | S 235 | S 235 | S 550 |
| Klassifizierung | |||
|---|---|---|---|
| c/t | 28,5 | 46 | 35,68 |
| Querschnittsfläche [cm²] | 79,95 | 70,17 | 60,99 |
| Spannung [kN/cm²] | -12,51 | -14,25 | -16,40 |
| Spannungsverhältnis | 1,0 | 1,0 | 1,0 |
| Materialbeiwert | 1,0 | 1,0 | 0,65 |
| max. c/t Klasse 1 | 33 | 33 | 21,57 |
| max. c/t Klasse 2 | 38 | 38 | 24,84 |
| max. c/t Klasse 3 | 42 | 42 | 27,45 |
| Querschnittsklasse | 1 | 4 | 4 |
| Wirksame Querschnittswerte | |||
| 0,81 | 0,97 | ||
| 0,89 | 0,8 | ||
| beff = ρ ∙ b [cm] | 24,81 | 17,98 | |
| A bzw. Aeff [cm²] | 79,95 | 63,51 | 49,79 |
| Nachweis Biegeknicken | |||
| [kN] | 1.745,66 | 2.089,14 | 1.246,46 |
| Npl = A ∙ fy bzw. Aeff ∙ fy [kN] | 1.878,83 | 1.492,49 | 2.738,45 |
| 1,04 | 0,85 | 1,48 | |
| Imperfektionsbeiwert α | 0,21 (KSL a) | 0,21 (KSL a) | 0,13 (KSL a0) |
| Φ = 0,5 ∙ [1 + α (λ - 0,2) + λ²] | 1,13 | 0,93 | 1,68 |
| 0,639 | 0,769 | 0,404 | |
| [kN] | 1.091,4 | 1.043,4 | 1.005,8 |
| 0,92 | 0,96 | 0,99 | |
Alle drei Stützen sind tragfähig für die angegebene Belastung. Die mittlere Stütze besitzt größere Aussenmaße, ist jedoch wesentlich schlanker ausgeführt. Der Querschnitt fällt daher in die Querschnittsklasse 4 und der Nachweis ist mit einer effektiven Querschnittsfläche nach EN 1993-1-5 zu führen. Es ergibt sich eine Abminderung um 11 % aufgrund lokalen Beulens. Die größeren Außenabmessungen wirken sich jedoch positiv auf die Verzweigungslast Ncr aus. Daraus resultiert ein günstigerer bezogener Schlankheitsgrad für Biegeknicken dieser Stütze.
Bei der mittleren Stütze (Stab 2) werden gegenüber der linken Stütze zirka 12 % an Querschnittsfläche bei gleicher Stahlgüte eingespart.
Im Vergleich zur mittleren Stütze können mit der rechten Stütze (Stab 3) nochmals etwa 13 % der Querschnittsfläche eingespart werden. Die kleineren Abmessungen wirken sich negativ auf die Verzweigungslast aus. Auch fallen 20 % der Querschnittsfläche aufgrund lokalen Beulens aus. Der bezogene Schlankheitsgrad dieser Stütze ist erheblich schlechter als bei den anderen Stützen, obwohl Ncr mit der realen Querschnittsfläche berechnet werden darf. Der Nachweis gelingt aufgrund der größeren Streckgrenze trotzdem.
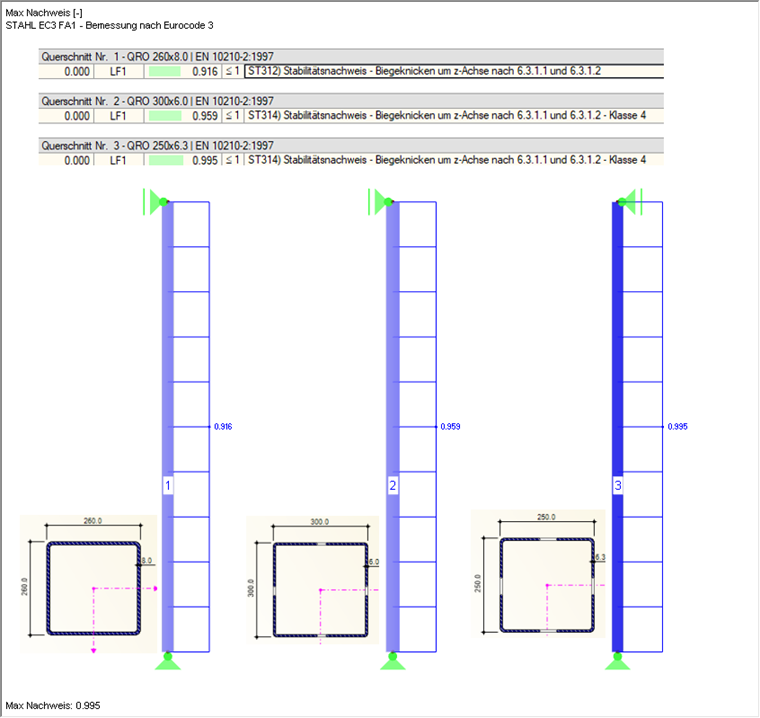
Die Bemessungsergebnisse mit RF-/STAHL EC3 sind in Bild 02 ersichtlich.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
