Fire
The fire is an action on the structure and thus it is regulated with all boundary conditions in EN 1991-1-2. This standard also includes all nominal temperature-time curves and simple natural fire models that can act on a structure.
Nominal Temperature-Time Curves
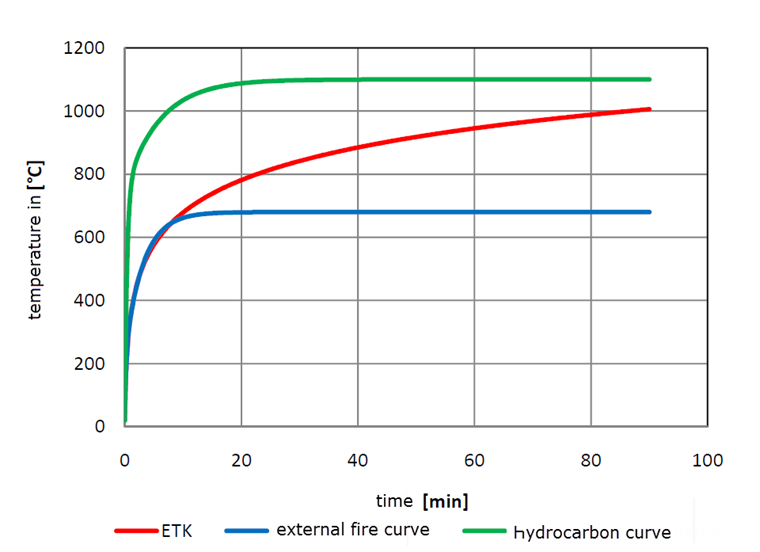
Over the years, many fire tests were done to evaluate the behavior of structural components in the case of fire. During the tests, it was possible to determine the development of a fire over time and the temperature curve depending on the fire load and the components and materials. These temperature-time curves are applicable only up to a certain point as they do not include any fire development phase nor cooling phase. Due to these tests and for the sake of a standard uniform assessment, a temperature-time law based on international agreements has been codified. DIN EN 1991-1-2 provides three fire curve concepts which may be used for the simplified method according to DIN EN 1993-1-2.
Standard Time-Temperature Curve (ETK):
Θg = 20 + 345 ∙ log10(8 ∙ t +1)
αc = 25 ∙ [W / (m ∙ K)]
External Fire Curve:
Θg = 660 ∙ (1 - 0.687 ∙ e0.32 ∙ t - 0.313 ∙ e-3.8 ∙t) + 20
αc = 25 ∙ [W / (m ∙ K)]
Hydrocarbon Fire Curve:
Θg = 1,060 ∙ (1 - 0.325 ∙ e-0.167 ∙ t - 0.675 ∙ e-2.5∙ t) + 20
αc = 50 ∙ [W / (m ∙ K)]
Furthermore, there is a parametrized fire curve, but this is intended to use for the general design of fire protection according to DIN EN 1993-1-2. In this case, the standard time-temperature curve is the most widely used fire curve, because most of the experimental studies on fire protection materials were performed according to this curve. In contrast, the external fire curve is not of a high importance as the temperature of this curve rises up to 660 °C and therefore, it is not suitable for a longer time of fire exposure with the fire protection material. The hydrocarbon fire curve is similar to the tunnel fire curve as the temperature of this curve rises up to 1350 °C and the increase is even steeper than in the case of any other fire curve.
Parametric Fire Exposure
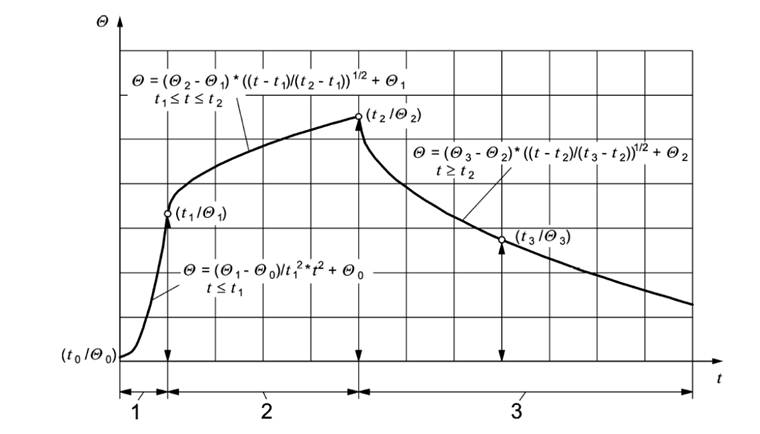
If parametric fire exposure is used as a fire scenario, the load reduction effect of the structural component must be ensured. No failure of the component should occur during the fire phase, including the cooling phase, or within the required fire resistance time. Appendix A of EN 1991-1-2 provides a parametric temperature-time curve. This fire scenario is no longer permitted in Germany as there is the binding National Annex to EN 1991-1-2 that must be applied. This scenario was replaced by design fire, This allows for a complete description of a possible fire scenario; that is: from the development phase to the compartment fire phase to the decay phase.
The curve sections are limited by distinctive points that result in the distribution of the rate of heat release. When determining temperature values, it is necessary to distinguish between ventilation controlled fires and fuel controlled fires. Moreover, the application of this natural fire model is limited. It applies to surface areas with an area of up to 400 m² and a height of up to 6 m. In the case of the ventilation controlled design fires, the characteristic value of the maximum rate of heat release can be calculated using the equations provided in Appendix A.