Structural Fire Design According to DIN EN 1993-1-2 (Thermal Material Properties)

The material properties of structural steel are described in EN 1993‑1‑2 [2] using functions in order to have an accurate value for each property at each temperature.

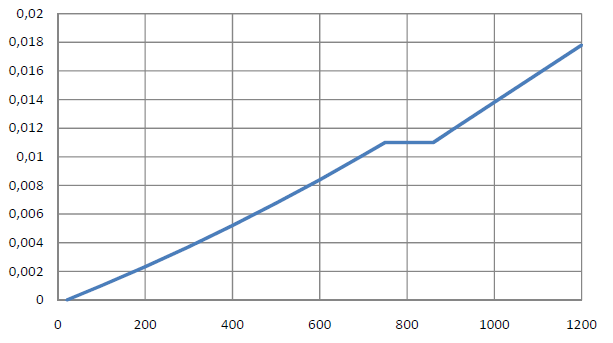
Thermal Expansion

The thermal expansion Δl/l is a change in geometrical dimensions caused by the temperature change.

At 20 °C ≤ Θ_a < 750 °C:

At 750 °C ≤ Θ_a ≤ 860 °C:

At 860 °C < Θ_a ≤ 1,200 °C:

Thermal Expansion of Steel

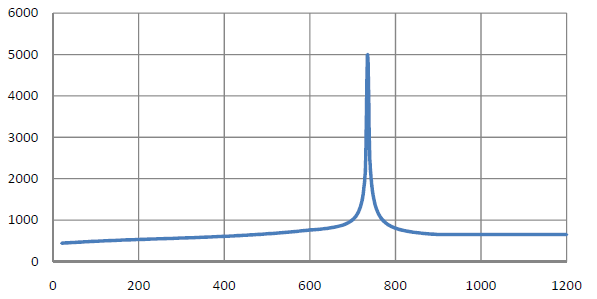
Specific Heat Capacity

The specific heat capacity c_a in J/(kgK) is the heat amount required to heat one kilogram of material by one Kelvin.

At 20 °C ≤ Θ_a < 600 °C:

At 600 °C ≤ Θ_a < 735 °C:

At 735 °C ≤ Θ_a < 900 °C:

At 900 °C ≤ Θ_a ≤ 1,200 °C:

Specific Heat Capacity of Steel

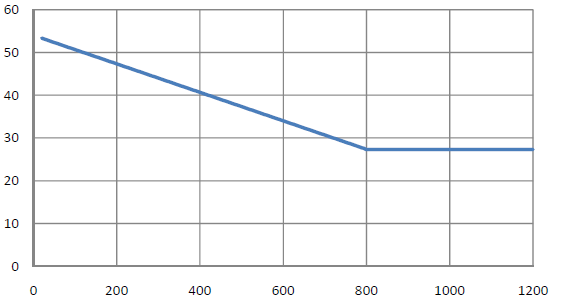
Thermal Conductivity

The thermal conductivity λ_a in W/(mK) describes the ability to transfer heat energy by means of heat transfer.

At 20 °C ≤ Θ_a < 800 °C:

At 800 °C ≤ Θ_a ≤ 1,200 °C:

Thermal Conductivity of Steel

Literature