This article describes the modeling of a Kármán vortex street in RWIND.
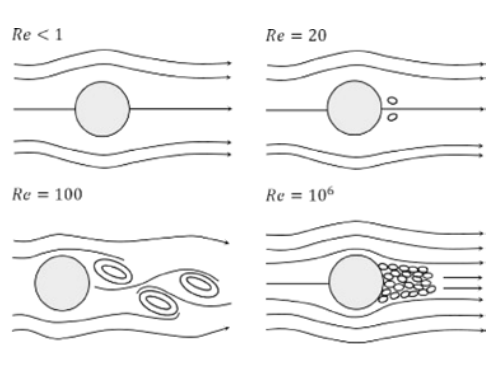
For certain Reynolds number ranges, a street of vortices is formed behind objects that are narrow but high. Especially in areas with many high-rise buildings and the trend towards narrow skyscrapers, these vortices can have an impact on the wind loads of the surrounding buildings. The following shows the vortex formation as a function of the Reynolds number according to [1].
The well-known vortex street develops on a Reynolds number basis of about 100. When the number increases, the flow becomes turbulent. So far, satisfactory results have only been achieved in a Reynolds number range that is too high. Find an example where Re = 10e7 below.
Hence, the inlet velocity had to be set much higher than calculated in order to trigger the desired behavior. An exact limit speed could be identified theoretically, but would require many individual simulations (even for a linearly increasing wind profile), which has been discarded for reasons of time. In addition, the vortex shedding frequency does not seem to conform to the theory. Since the shedding frequency depends on the Strouhal number and thus the inlet velocity, this behavior was to be expected.
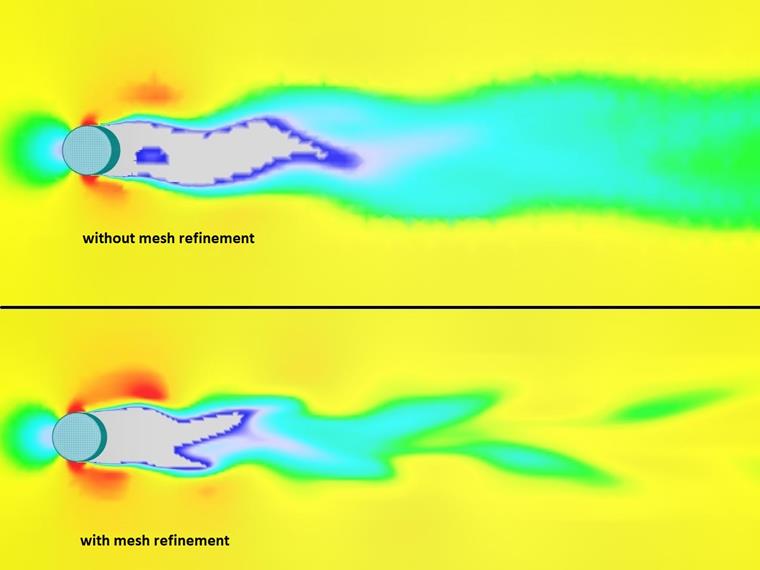
The mesh density is probably the most important influencing factor in the correct formation of a vortex street. In order to save resources, the mesh density in RWIND is reduced by increasing distance from the analyzed object in the wind tunnel. This simplification is very useful for individual buildings, but makes modeling the Kármán vortex street more difficult. Therefore, a mesh refinement makes sense, for example, of a section above the structure's height over the full length of the wind tunnel, starting with the structure's depth. The effect of such a refinement is shown below.
In the context of the present analysis, it has not been considered to what extent a mesh refinement affects the ultimate pressures on surrounding buildings. This needs further analysis using future modeling.
Due to an adapted coloring and a refined mesh, the following picture is the result. The slightly tilted view enables a better distinction between the different shades of red.
What is interesting is the direction of the velocity vectors. The greatest turbulence, which is directly behind the structure, shows the desired chaotic distribution of the directional vectors, as would be expected with a vortex. However, smaller vortices at a greater distance from the structure do not show this behavior. Though the false-color image of the absolute velocity distribution may indicate smaller vortices, all direction vectors point in the direction of the inflow. In terms of fluid mechanics, this behavior is absurd, but no specific cause can be identified.
Further optimization of the vortex street would be possible by a mesh which is refined once again. It is also conceivable that an even finer refinement could also correct the anomaly of the directional vectors. However, this is reflected in a significantly higher memory and computing requirement. A mesh refinement that is as small as possible but as large as necessary would be advisable. The cylinder's top third, including a sufficient distance to the top nodes, would probably be best suited for this.
All in all, the modeled vortex street shows relatively good results with regard to the velocity and thus the pressure profile. In detail, such as the directional vector distribution and the emission frequency, the approach presented in this article probably fails due to the limitations of the solver itself. It is advisable to repeat this calculation with the latest versions of RWIND.