Este artículo describe el modelado de una calle de vórtices de von Kármán en RWIND.
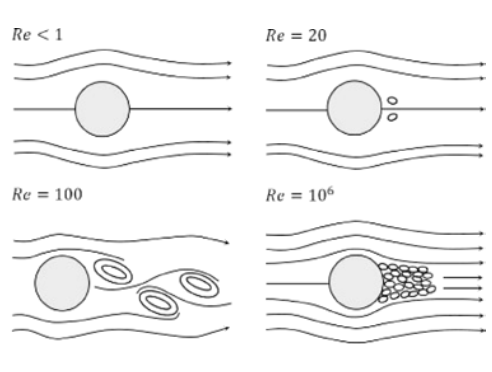
Para ciertos rangos de números de Reynolds, se forma una calle de vórtices detrás de objetos que son estrechos pero altos. Especialmente en áreas con muchos edificios de gran altura y la tendencia hacia rascacielos estrechos, estos vórtices pueden tener un impacto en las cargas de viento de los edificios circundantes. A continuación se muestra la formación de vórtices en función del número de Reynolds según [1].
La conocida calle de vórtices se desarrolla sobre una base de números de Reynolds de aproximadamente 100. Cuando el número aumenta, el flujo se vuelve turbulento. Hasta ahora, solo se han logrado resultados satisfactorios en un rango de números de Reynolds que es demasiado alto. Puede encontrar un ejemplo donde Re = 10e7 a continuación.
Por lo tanto, se tuvo que establecer la velocidad de entrada mucho más alta de lo calculado para activar el comportamiento deseado. Teóricamente se podría identificar una velocidad límite exacta, pero se requerirían muchas simulaciones individuales (incluso para un perfil de viento que aumenta linealmente), lo que se ha descartado por razones de tiempo. Además, la frecuencia de desprendimiento de vórtices no parece corresponder a la teoría. Dado que la frecuencia de separación depende del número de Strouhal y, por lo tanto, de la velocidad del flujo, era de esperar este comportamiento.
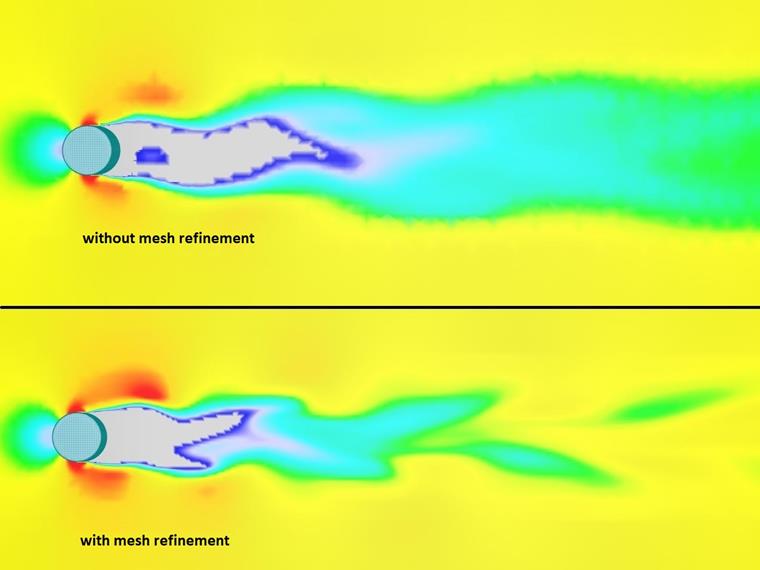
Probablemente el factor de influencia más importante para la correcta formación de una calle de vórtices sea la densidad de la malla. Para ahorrar recursos, la densidad de la malla en RWIND se reduce al aumentar la distancia a partir del objeto analizado en el túnel de viento. Esta simplificación es muy útil para edificios individuales, pero dificulta el modelado de la calle de vórtices de von Kármán. Por lo tanto, cobra sentido un refinamiento de la malla, por ejemplo, de una sección por encima de la altura de la estructura en toda la longitud del túnel de viento, comenzando con la altura de la estructura. El efecto de tal refinamiento se muestra a continuación.
En el contexto del presente análisis, no se ha considerado hasta qué punto un refinamiento de la malla afecta las presiones últimas en los edificios circundantes. Esto necesita un análisis más detallado utilizando modelos futuros.
Gracias a un colorido adaptado y una malla refinada, el resultado es la siguiente imagen. La vista ligeramente inclinada permite una mejor distinción entre los diferentes tonos de rojo.
Lo interesante es la dirección de los vectores de velocidad. La mayor turbulencia, que se encuentra directamente detrás de la estructura, muestra la distribución caótica deseada de los vectores direccionales como se esperaría con un vórtice. Sin embargo, los vórtices más pequeños a una mayor distancia de la estructura no muestran este comportamiento. Aunque la imagen en falso color de la distribución de velocidad absoluta puede indicar vórtices más pequeños, todos los vectores de dirección apuntan en la dirección del flujo de entrada. En términos de mecánica de fluidos, este comportamiento es absurdo, pero no se puede identificar una causa específica.
Sería posible una mayor optimización de la calle de vórtices mediante una malla que se vuelva a refinar. También es concebible que un refinamiento aún más fino también pueda corregir la anomalía de los vectores direccionales. Sin embargo, esto se refleja en un requerimiento de memoria y computación significativamente mayor. Sería aconsejable un refinamiento de la malla lo más pequeño posible pero tan grande como fuese necesario. El tercio superior del cilindro incluyendo una distancia suficiente a los nudos superiores, probablemente sería lo más adecuado para esto.
Con todo, el modelado de la calle de vórtices muestra resultados relativamente buenos con respecto a la velocidad y, por lo tanto, al perfil de presiones. En detalle, como la distribución del vector direccional y la frecuencia de emisiones, es probable que el planteamiento presentado en este artículo falle debido a las limitaciones del solucionador en sí. Se recomienda repetir este cálculo con las últimas versiones de RWIND.
[1] Imagen de la calle Karman vortex y el número de Reynolds
.png?mw=350&hash=f79867dbf405d536638daef39ee25b113e6e540d)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
