Opcjonalnie, norma EN 1993-1-1, Rozdział 5.2.1 (4), wyrażenie 5.2 zawiera uproszczone obliczenia dla ruchomych konstrukcji ramowych w budynkach (ramy portalowe o małym nachyleniu dachu < 26° oraz ramy płaskie w budynkach ):
Gdzie
HEd = całkowite obliczeniowe obciążenie poziome (w tym potencjalne ścinanie kondygnacji)
VEd = całkowite obliczeniowe obciążenie pionowe (w tym potencjalny nacisk kondygnacji)
δH, Ed = przemieszczenie poziome w górnej części kondygnacji w stosunku do spodu kondygnacji, poddane działaniu HEd
h = wysokość kondygnacji
Takie podejście ma zastosowanie, jeżeli wpływ ściskania osiowego w krokwiach na obciążenie krytyczne jest niewielki. Można to sprawdzić za pomocą wyrażenia 5.3, o którym mowa w uwadze 2B:
Równanie to odpowiada dokładnie elementowi (739) normy DIN 18800-1, ale z odwrotnym warunkiem.
Podstawą tej metody jest analiza P-delta. Wyrażenie 5.2 można jednak również wyprowadzić ze współczynnika Dischingera przez stosunek momentu początkowego M0 do momentu dodatkowego ∆M:
Przykład
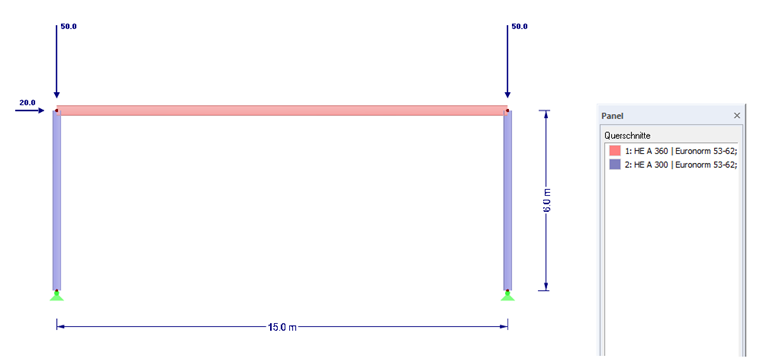
Obliczenia zilustrowano na poniższym przykładzie ruchomej ramy.
.png?mw=760&hash=acc6a96b53f58aee73eefe3d9e14a16d856b5b6d)
Te wartości początkowe są używane w równaniu 5.2, skutkując współczynnikiem obciążenia krytycznego wynoszącym:
Moduł RF-STABILITY (liniowy solwer wartości własnych) lub RSBUCK umożliwia szybkie określenie dokładnego wyniku współczynnika obciążenia krytycznego oraz kształtu modalnego z brakiem stabilności antymetrycznej.
.png?mw=760&hash=612208b5e1fef1338f89efe8f7394f1d23b20063)
.png?mw=350&hash=616d09fd0ed02d251d14e9c6ea384af2cb1ed9fb)
.png?mw=350&hash=684b922aa6b0b676a221915132500287a0a21c2e)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
