Optional bietet die EN 1993-1-1 in Abschnitt 5.2.1 (4) mit der Gleichung 5.2 eine vereinfachte Ermittlung für verschiebliche Rahmensysteme des Hochbaus (Hallenrahmen mit geringer Dachneigung < 26 ° und Rahmentragwerke des Geschossbaus) an:
mit
HEd = Bemessungswert der gesamten horizontalen Lasten (einschließlich gegebenenfalls Stockwerksschub)
VEd = Bemessungswert der gesamten vertikalen Lasten (einschließlich gegebenenfalls Stockwerksschub)
δH,Ed = Horizontalverschiebung der oberen Stockwerksknoten gegenüber den unteren infolge HEd
h = Stockwerkshöhe
Das Verfahren gilt unter der Voraussetzung, dass der Einfluss der Riegelnormalkraft auf die Verzweigungslast klein ist. Dies wird mit Gleichung 5.3 in der Anmerkung 2B überprüft:
Diese Gleichung entspricht exakt dem Element (739) der DIN 18800-1, nur mit umgekehrter Bedingung.
Grundlage des Verfahrens ist das sogenannte P-δ-Verfahren. Die Gleichung 5.2 ließe sich jedoch auch aus dem Dischinger-Faktor durch das Verhältnis von Ausgangsmoment M0 zu Zusatzmoment ∆M herleiten:
Beispiel
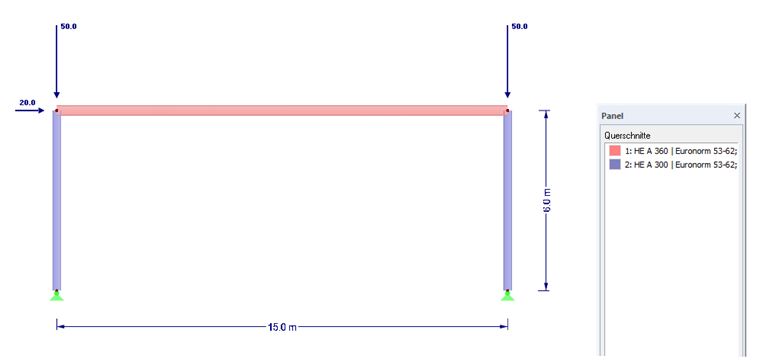
An folgendem verschieblichen Rahmen soll die Berechnung beispielhaft aufgezeigt werden.
Mit diesen Eingangswerten ergibt sich nach Gleichung 5.2 ein Verzweigungslastfaktor von:
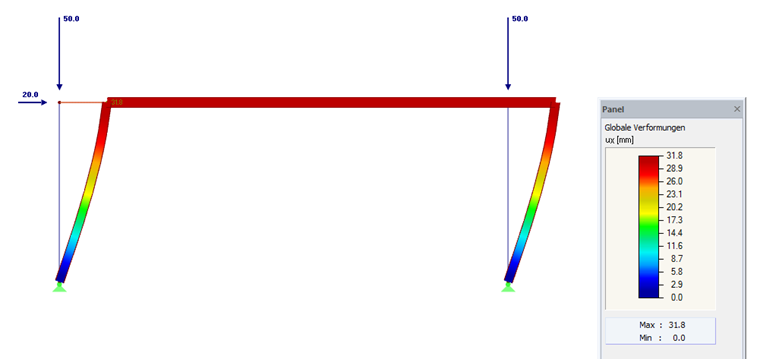
Mit RF-STABIL (linearer Eigenwertlöser) oder RSKNICK lässt sich das exakte Ergebnis für den Verzweigungslastfaktor sowie die Eigenform mit einem antimetrischen Stabilitätsversagen schnell ermitteln.