V EN 1993-1-1, čl. 5.2.1 (4), výraz 5.2 je volitelně uveden zjednodušený výpočet pro pohyblivé rámové konstrukce v budovách (portálové rámy s mělkým sklonem střechy < 26° a rovinné rámy typu nosník a sloup v budovách ):
kde
HEd = celkové návrhové vodorovné zatížení (včetně případného smykového namáhání)
VEd = celkové návrhové svislé zatížení (včetně případného tahového zatížení)
δH, Ed = vodorovný posun v horní části podlaží vzhledem ke spodní části podlaží vystavené HEd
h = výška podlaží
Tento postup se uplatní, pokud je účinek podélného tlaku v krokve na kritické zatížení malý. To lze zkontrolovat pomocí výrazu 5.3 uvedeného v poznámce 2B:
Tato rovnice přesně odpovídá prvku (739) podle DIN 18800-1, ale s obrácenou podmínkou.
Základem této metody je analýza P-delta. Pro vyjádření výrazu 5.2 lze ovšem také z Dischingerova součinitele odvodit vztah počátečního momentu M0 k přídavnému momentu ∆M:
Příklad
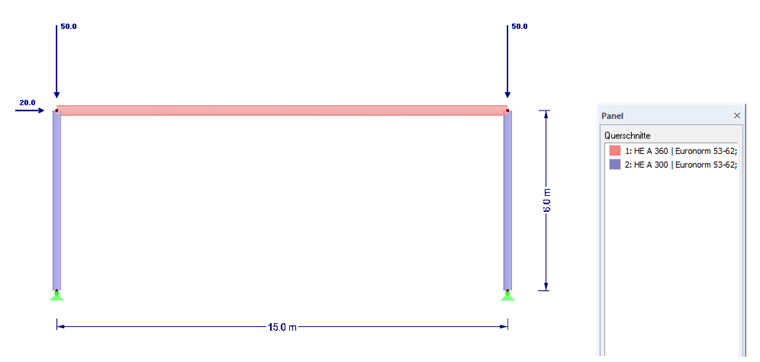
Výpočet je znázorněn na následujícím příkladu pohyblivého rámu.
.png?mw=760&hash=acc6a96b53f58aee73eefe3d9e14a16d856b5b6d)
Tyto počáteční hodnoty se použijí v rovnici 5.2, z čehož vyplývá součinitel kritického zatížení:
Modul RF-STABILITY (lineární řešič vlastních čísel) nebo RSBUCK umožňuje rychle určit přesný výsledek součinitele kritického zatížení a také tvar režimu při porušení antimetrické stability.
.png?mw=760&hash=612208b5e1fef1338f89efe8f7394f1d23b20063)
.png?mw=350&hash=616d09fd0ed02d251d14e9c6ea384af2cb1ed9fb)
.png?mw=350&hash=684b922aa6b0b676a221915132500287a0a21c2e)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
