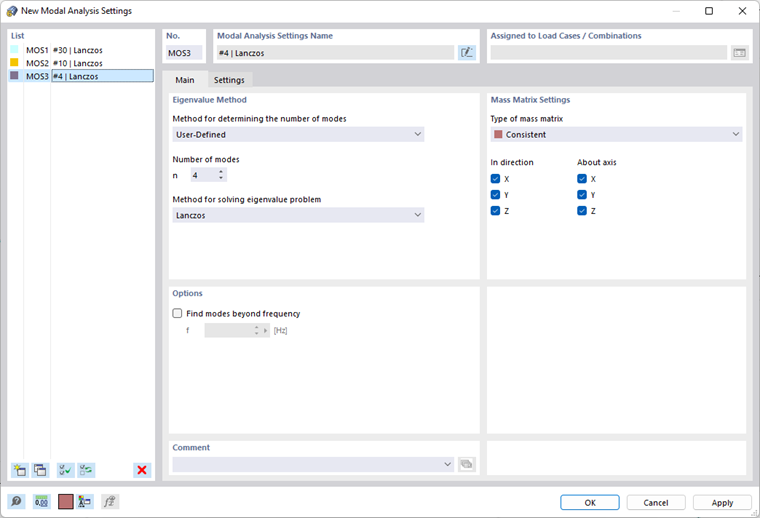
在“模态分析”设置中可以指定计算特征值所依据的规则, 预设了两种标准分析类型。 用户可以随时在“模态分析”对话框中进行设置。
基本
基本选项卡管理着模态分析所需的设置,以及一些其他基本计算参数。 RFEM 和 RSTAB 提供了不同的特征值法选项。
特征值法
在这一部分中,您可以定义使用哪种方法分析特征值问题,以及确定多少个模态。
确定振型数目的方法
可以从列表中的三个选项中进行选择。
- 用户自定义
用户自定义方法允许用户指定要计算的最小振型的数目。 在该模块中最多可以定义 9999 个振型。 除了这个限制外,模型还代表了对可能的振型数量的限制: 它对应于自由度与自由质量点的数量乘以质量作用方向的数量。
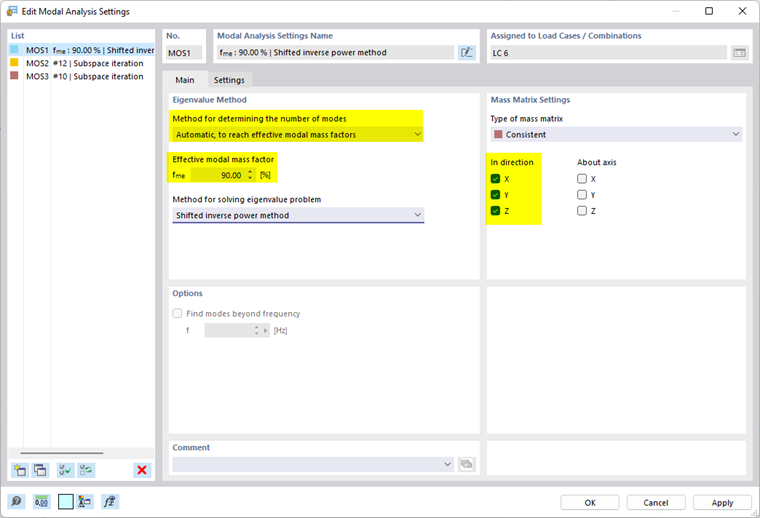
- 自动,以达到振型有效质量系数
程序会根据需要定义足够多的振型,直到达到指定的振型质量系数。 并指定平动方向(X,Y,Z)的振型有效质量系数。
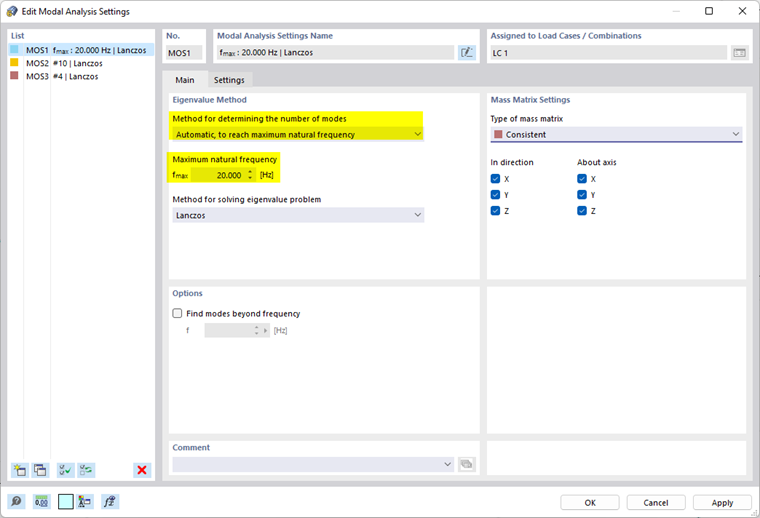
- 自动,以达到最大自振频率
程序会根据需要确定足够多的振型,直到达到指定的自振频率。
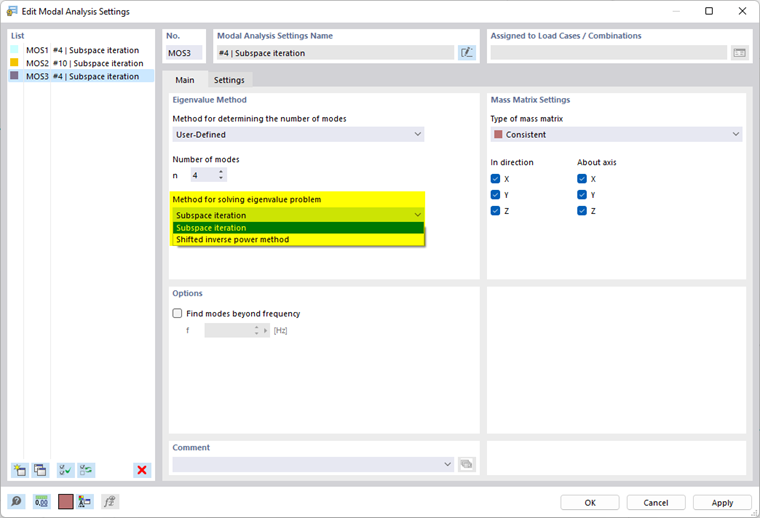
求解特征值问题的方法 (RFEM)
用户可以在列表中选择三种求解特征值问题的方法。 如果您设置了自动确定特征值个数,那么只有一种求解方法可用。
每种方法的详细信息可参见 Bathe [[]]#Refer [1]]] 和 Natke [2]。
- Lanczos
Lanczos 方法适用于计算大型模型的最低特征值和相应的振型。 在大多数情况下,该算法可以快速收敛。 最多可以计算 n-1 个振型 ( n : 有质量的模型的自由度)。
在 en.wikipedia.org/wiki/Lanczos_algorithm 上可以找到介绍性的描述。
- 特征多项式的根
该方法是特征值问题的解析解。 这种方法的主要优点是可以计算出较高特征值的精度,并且可以确定模型的所有特征值。 对于较大的模型,此方法非常耗时。
在 https://de.wikipedia.org/wiki/characteristic_polynomial 上关于介绍性的描述。
- 子空间迭代
该方法可以一次计算出所有特征值。 刚度矩阵的波动范围会影响计算时间。 该方法仅适用于大型有限元模型,并且需要计算很少特征值的情况下。 工作记忆会限制在合理时间内可以确定的特征值的数量。
在 en.wikipedia.org/wiki/Krylov_subspace 上有介绍性的描述。
求解特征值问题的方法(RSTAB)
列表中提供了两种求解特征值问题的方法。 如果用户选择了一种自动计算特征值个数的方法,那么只有一种求解方法可用。
每种方法的详细信息请参见Bathe {%!#Refer [1]]]。
- 子空间迭代
该方法可以一次计算出所有特征值。 刚度矩阵的波动范围会影响计算时间。 该方法仅适用于大型有限元模型,并且需要计算很少特征值的情况下。 工作记忆会限制在合理时间内可以确定的特征值的数量。
在 en.wikipedia.org/wiki/Krylov_subspace 上有介绍性的描述。
- 转换反幂法
该方法是基于对振型特征向量的假设,在计算过程中通过迭代将其逼近到收敛解。 这种方法的优点是收敛速度快,计算时间短。 “移位” 表示该方法也可用于确定给定矩阵的最大和最小特征值之间的所有结果。
在 en.wikipedia.org/wiki/Inverse_iteration 上可以找到介绍性的说明。
质量矩阵设置
用户可以在该面板中定义模态分析中使用的质量矩阵,以及质量所在的轴或质量轴。
质量矩阵的类型:
用户可以在该列表中选择三种质量矩阵。
- 斜向加劲肋
用户的质量矩阵 M 为对角线,假定质量集中在有限元节点上。 在矩阵中输入 X、Y 和 Z 平动方向上的集中质量,以及绕全局坐标轴 X (φX )、Y (φY ) 和 Z (φZ ) 转动方向上的集中质量。 这里要区分下面两种情况:
– 只有平动自由度的对角矩阵: 如果对角矩阵只有平动方向激活,则对角矩阵为:
– 具有平移和转动自由度的对角矩阵: 如果激活了平动方向和转动方向,对角矩阵有:
- 一致
一致质量矩阵是有限元的完备质量矩阵。 因此,质量并不集中在有限元节点上。 而是使用形状函数来得到更真实的有限元单元质量分布。 在该质量矩阵中考虑质量矩阵中的非对角线元素, 一致质量矩阵的结构如下(为简化计算,形状函数被忽略):
- 单位
单位矩阵覆盖之前定义的所有质量。 该矩阵是一致矩阵,其中所有对角线元素都是 1 kg。 每个有限元节点的质量都设为 1。 考虑质量的平移和旋转。 这种数学方法只能用于数值分析。
更多关于矩阵类型,特别是单位矩阵的使用的信息可以在 Barth/Rustler 找到[3]。
沿方向/绕轴
六个复选框控制在确定特征值时质量作用的方向或轴。 质量可以作用在全局的 X、Y 或 Z 方向上,并绕 X、Y 和 Z 轴旋转。 勾选相关复选框。 【线振型】需要激活至少一个方向或轴才能计算特征值。
选项
该对话框位于“基本”选项卡中,是模态分析的重要设置选项。
寻找振型超过频率
如果模型中单个杆件或面的自振频率非常低,则它们首先以局部振型的形式出现。 如果选择该复选框,则只计算大于特定固有频率值 "f" 的特征值。 通过这种方式,可以减少结果数量,并将结果数量限制为与全局模型相关的特征值。
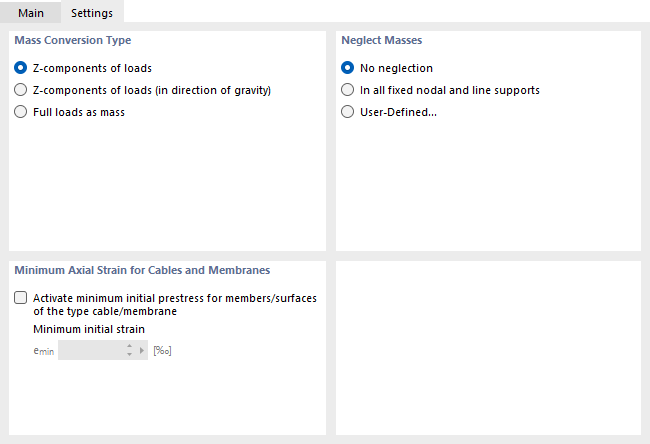
设置
在设置选项卡中可以管理模态分析所需的进一步设置,以及基本计算参数。
质量转换类型
在该对话框部分可以导入质量用于模态分析。 默认情况下只考虑“'荷载的 Z 分量”。 荷载分量同时作用在 Z 轴的正方向和负方向上。
使用“荷载的分量 Z(重力方向)”选项,程序只应用荷载分量在重力方向上的作用。 引力由全局 Z 轴的方向确定(见章节 轴方向 ): 全局荷载向导的长度方向为全局坐标系 Z 轴的全局坐标系。 如果全局 Z 轴向上,则相反
如果选择“完全荷载作为质量”选项,则将所有荷载导入所有部分,作为质量导入。
忽略质量
模态分析考虑了模型中定义的所有质量。 用户可以在对话框该部分忽略模型各部分的质量,例如所有固定的节点支座和线支座的质量。 使用该功能可以定义一个用户自定义的对象。
当选择“用户自定义”选项时,会出现附加选项卡“忽略质量”。 您可以在此处指定没有质量的对象。
用户可以使用对象编号直接创建对象(节点、线、杆件等)的列表。 或者,可以使用
![]() 对象列表输入栏中的按钮,可以以图形方式选择对象。 点击
对象列表输入栏中的按钮,可以以图形方式选择对象。 点击
![]() 按钮,以仅预设固定支座。
按钮,以仅预设固定支座。
使用位移方向 uX 、uY和 uZ ,以及转角 φX 、φY和 φZ的复选框来定义忽略质量的方向。
尽管如此,在矩阵中仍考虑了忽略质量的对象的刚度。 如果您还想忽略这些对象的刚度,则可以使用 结构调整来单独调整刚度。 在计算中可以停用对象(见章节 )。
索膜的最小轴向应变
正确的输入是和 膜面 对长度有最小变化要求。 如果该值设置得太低,则计算得出的振型不符合实际,并且只能计算出局部振型。 初始预应力 emin的默认值适用于大多数情况。