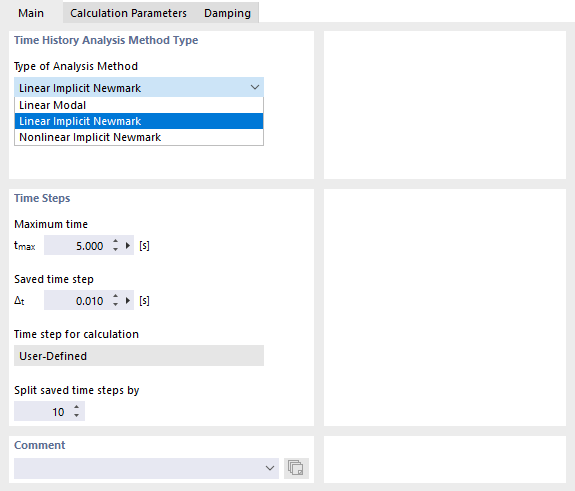
基础选项卡管理过程和时间步长的预设。
时间历程分析方法类型
在 RFEM 中,列表中提供了两种线性和一种非线性分析方法可供选择(参见图 设定验证方法及时间步长):
- 线性模态
- 线性隐式Newmark分析
- 非线性隐式Newmark分析
在 RSTAB 中,列表中包含了两种线性和两种非线性分析方法:
- 线性模态
- 线性隐式Newmark分析
- 非线性显式 | 一阶
- 非线性显式 | 三阶
前两种分析方法是几何线性的,因此仅对小变形有效。此外,模型的所有非线性特性都被忽略(例如,不考虑支座的失效)或替换(拉杆用桁架杆表示)。
线性模态分析方法 使用一个基于模型特征值和特征模式的解耦系统,并在分配的 模态分析工况 中确定。多自由度系统("MDOF")被分解为多个单自由度系统("SDOF")(对角化的质量和刚度矩阵)。需要一定数量的特征值以保证精度。随后,使用隐式Newmark求解器确定解耦系统的解。质量矩阵和刚度变化的设置由分配的模态分析工况继承。如果特征值已经确定,该分析方法比线性隐式Newmark分析稍快。
线性隐式Newmark分析 是一种直接时间积分方法。需要足够小的时间步长以获得精确结果。在此分析方法中不需要固有振动分析。理论背景详见 [1]。通过隐式求解方法,根据时间 i 和 i + 1 的值确定时间 i + 1 的未知值。解决非线性方程,不需要迭代和收敛控制。
非线性隐式Newmark分析 考虑了模型的几何和结构非线性。该方法绝对稳定:时间步长 Δt 没有上限限制。然而,为了获得精确结果,还是需要足够小的时间步长。时间增量取决于激励、模型频率和非线性的复杂性。对于质量矩阵和Rayleigh阻尼没有限制。
非线性显式方法 是RSTAB使用的中央差分法。它适用于短期激励和模型中快速变化的非线性。方法是唯一的,因为未知的值仅基于时间 i,而不基于时间 i + 1 的未知响应。显式积分规则在与对角质量矩阵和限制阻尼矩阵 C = αM 结合时运行良好。该方法是条件稳定的:仅当时间增量 Δt 小于稳定时间增量 Δtstabil 时,才会达到有限解。稳定限可以根据模型中最大的特征值 ωmax 和最大特征模式的临界阻尼比 D 定义。
在实际应用中,稳定时间增量可以通过以下估计值来确定:
对于线性弹性材料(泊松比为零),膨胀波速度计算如下:
此估计值允许比精确的 稳定性限值 更小的时间步长。然而,需注意许多效应不会被捕获,并且出于精度考虑,可能需要更小的时间步长 Δt。程序使用固定的时间步长—稳定的初始时间增量或用户自定义的值。
时间步长
输入用于计算的 '最大时间' tmax。然后在 '存储的时间步长' 字段中设定一个间隔 Δt,在此间隔内存储结果。这些时间步长将提供结果。动态包络线也由存储的时间步长构成。
除了必须存储的时间步长,还需设定实际的计算时间步长。在 '存储时间步长除以' 字段中输入一个值,用其将存储的时间步长 Δt 平分。
为了成功的时间历程方法,应选择“适当”的时间步长。最终,决定是计算时间和精度的妥协。对于线性时间历程方法,可以作出以下建议(参见 [2]):
- 考虑加速度时程和瞬态时间图表,离散激励的最短长度应至少分为七个时间步长。
- 对于时间步长的计算,应使用对系统响应相关的模型的最高频率 f,方法如下:Δt ≤ 1 / (20f)。类似地,应检查激励的最大频率是否在条件 Δt ≤ 𝜋 / (10ω) 中涵盖。如果没有,应调整时间步长。