Paramètres pour l'analyse modale

Un paramètre pour l'analyse modale (MOS) spécifie les règles selon lesquelles les valeurs propres sont calculées. Deux types d'analyse standard sont prédéfinis. Vous pouvez ajuster ces types à tout moment ou créer des paramètres supplémentaires pour l'analyse modale.

Général

L'onglet Général permet de gérer les paramètres pour l'analyse modale ainsi que les paramètres de calcul élémentaires. Pour RFEM et RSTAB, il existe différentes options pour choisir la méthode des valeurs propres.

Méthode des valeurs propres

Dans cette section, vous pouvez spécifier la méthode utilisée pour étudier le problème des valeurs propres et le nombre de modes propres déterminés.

Méthode pour la détermination du nombre de valeurs propres

Vous avez le choix entre trois options.

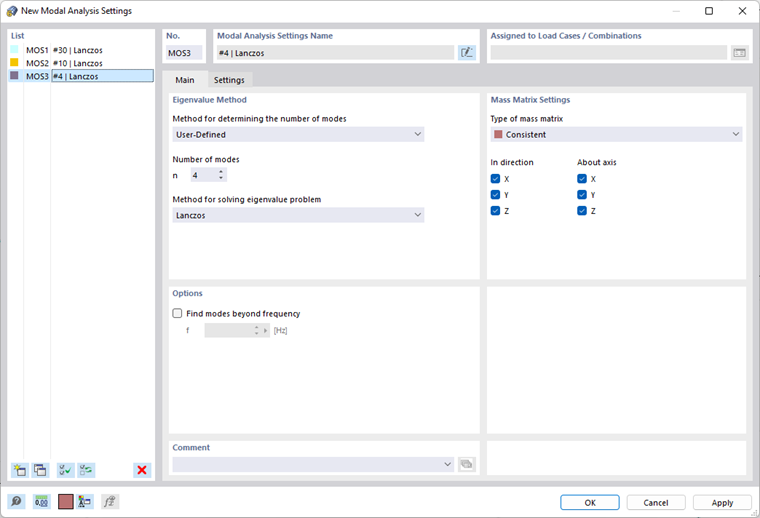
• Défini par l'utilisateur

Avec la méthode définie par l'utilisateur, vous pouvez spécifier le nombre de modes propres les plus petits à calculer. Jusqu'à 9 999 modes propres sont possibles. En plus de cette limite, le modèle représente également une limitation pour le nombre de modes propres possibles : Il correspond aux degrés de liberté résultant du nombre de points de masse libres multiplié par le nombre de directions dans lesquelles les masses agissent.

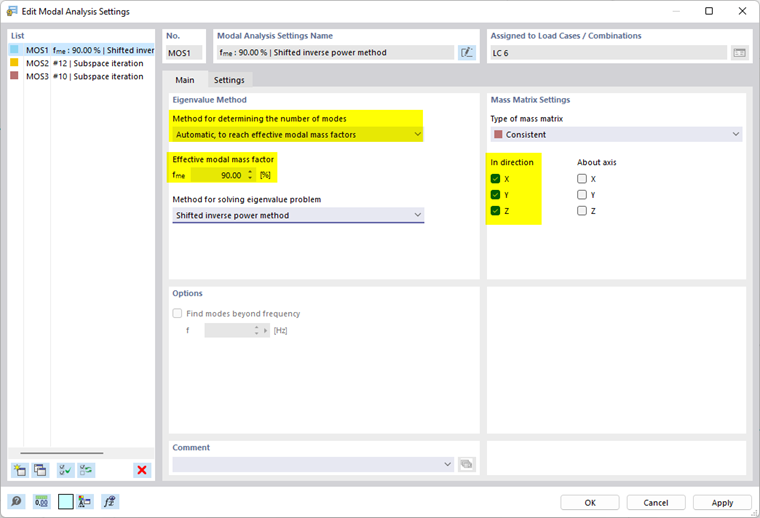
• Automatique, pour atteindre les facteurs de masses modales effectives

Autant de modes propres que nécessaire sont déterminés jusqu'à ce que le facteur de masse modale effective prédéfini soit atteint. Les facteurs de masse modale effective sont analysés pour les directions en translation spécifiées (X, Y, Z).

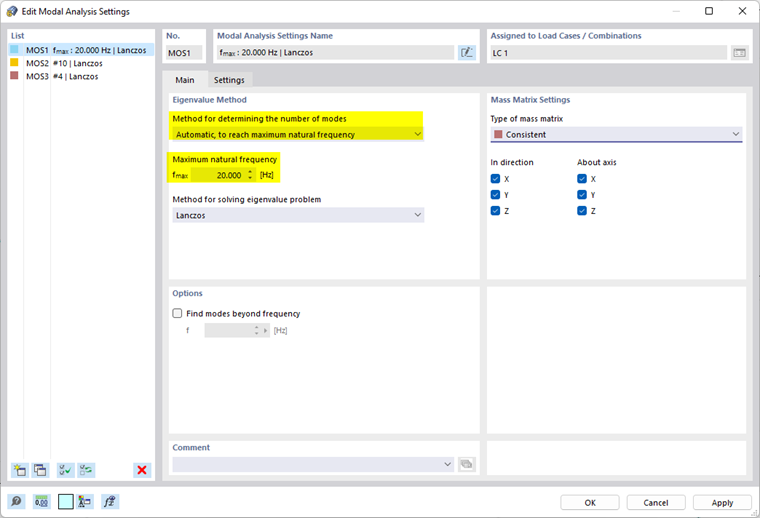
• Automatique, pour atteindre la fréquence propre maximale

Autant de modes propres que nécessaire sont déterminés jusqu'à ce que la fréquence propre prédéfinie soit atteinte.

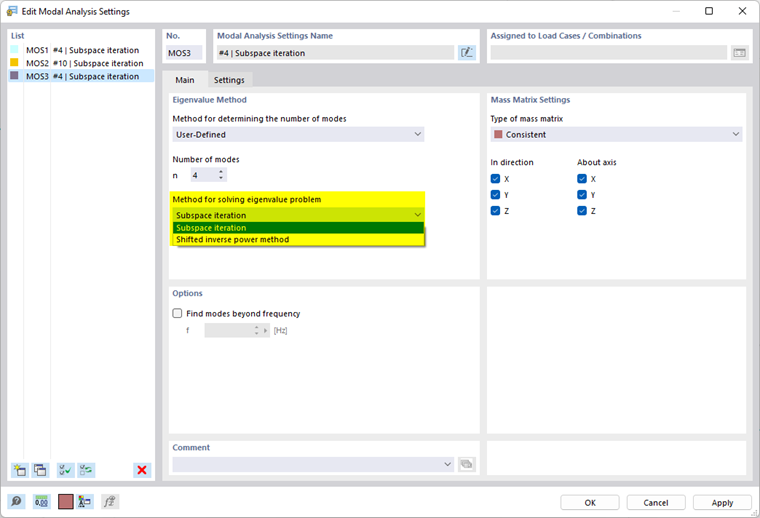
Méthode de résolution du problème des valeurs propres (pour RFEM)

Vous avez le choix entre trois méthodes pour résoudre le problème des valeurs propres. Si vous avez spécifié la méthode automatique de recherche du nombre de modes propres, une seule méthode de résolution est disponible.

Pour plus d'informations sur chaque méthode, voir Bathe [1] et Natke [2].

• Lanczos

La méthode de Lanczos convient comme méthode itérative pour déterminer les valeurs propres les plus faibles et les modes propres des grands modèles associés. Dans la plupart des cas, cet algorithme permet d'atteindre une convergence rapide. Vous pouvez calculer jusqu'à ⁿ/₂ modes propres (« n » : Nombre de degrés de liberté du modèle avec la masse).

Une description introductive est disponible ici : Algorithme de Lanczos.

• Racine du polynôme caractéristique

Cette méthode permet de résoudre un problème des valeurs propres selon une procédure directe. Le principal avantage de cette méthode est que les valeurs propres plus élevées peuvent être calculées plus précisément et que toutes les valeurs propres du modèle peuvent être déterminées. Pour les modèles plus grands, cette méthode peut être relativement longue.

Une description introductive est disponible ici : Polynôme caractéristique.

• Itération de sous-espace

Cette méthode permet de déterminer toutes les valeurs propres en une seule étape. Avec cette méthode, le spectre de la matrice de rigidité a une influence majeure sur la durée du calcul. Cette méthode n'est donc recommandée pour les grands modèles EF que si peu de valeurs propres doivent être calculées. La mémoire de travail limite le nombre de valeurs propres pouvant être déterminées avec un temps raisonnable.

Une description introductive est disponible ici : Sous-espace de Krylov.

Méthode de résolution du problème des valeurs propres (pour RSTAB)

Vous avez le choix entre deux méthodes pour résoudre le problème des valeurs propres. Si vous avez spécifié l'une des méthodes automatiques de recherche du nombre de modes propres, une seule méthode de résolution est disponible.

Pour en savoir plus sur chaque méthode, voir Bathe [1].

• Itération de sous-espace

Cette méthode permet de déterminer toutes les valeurs propres en une seule étape. Avec cette méthode, le spectre de la matrice de rigidité a une influence majeure sur la durée du calcul. Cette méthode n'est donc recommandée pour les grands modèles EF que si peu de valeurs propres doivent être calculées. La mémoire de travail limite le nombre de valeurs propres pouvant être déterminées avec un temps raisonnable.

Une description introductive est disponible ici : Sous-espace de Krylov.

• Itération inverse décalée

Cette méthode est basée sur des hypothèses pour les vecteurs propres des modes propres, qui sont approximées de manière itérative en une solution convergente au cours du calcul. L'avantage de cette méthode réside dans une durée de calcul courte grâce à la convergence rapide. « Décalée » signifie que cette méthode peut également être utilisée pour déterminer tous les résultats qui existent entre la plus grande et la plus petite valeur propre de la matrice donnée.

Une description introductive est disponible ici : Itération inverse.

Paramètres de la matrice de masse

Dans cette section, vous pouvez spécifier quelle matrice de masse est utilisée et dans quels axes les masses doivent agir dans l'analyse modale.

Type de matrice de masse

Vous avez le choix entre trois types de matrices de masse dans la liste.

• Diagonale

Dans le cas de la matrice de masse diagonale M, on présume que les masses sont concentrées sur les nœuds EF. Les entrées de la matrice sont les masses concentrées dans les directions de translation X, Y et Z ainsi que les directions de rotation autour des axes globaux X (φ_X), Y (φ_Y) et Z (φ_Z). Il faut distinguer les deux cas suivants :

- Matrice diagonale uniquement avec degrés de liberté en translation : Si seules les directions de translation sont activées, la matrice diagonale est la suivante :

- Matrice diagonale avec degrés de liberté en translation et en rotation : Si les deux directions de translation et de rotation sont activées, la matrice diagonale est la suivante :

• Constante

La matrice de masse constante est une matrice de masse complète d'éléments finis. Par conséquent, les masses ne sont pas concentrées sur les nœuds EF. Les fonctions d'approximation sont plutôt utilisées pour une distribution plus réaliste des masses au sein des éléments finis. Avec cette matrice de masse, les entrées non diagonales dans la matrice sont prises en compte, de sorte qu'une rotation des masses est généralement prise en compte. La matrice de masse constante est structurée comme suit (les fonctions d'approche sont négligées par souci de simplicité) :

• Unitaire

La matrice unitaire écrase les masses définies précédemment. Cette matrice est une matrice constante avec tous les éléments diagonaux pesant 1 kg. La masse est définie sur 1 à chaque point EF. Les translations et rotations des masses sont prises en compte. Cette approche mathématique ne doit être utilisée que pour des analyses numériques.

Pour plus d'informations sur les types de matrices et en particulier sur l'utilisation de la matrice unitaire, voir Barth/Rustler [3].

En direction/Autour de l'axe

Les six cases contrôlent dans quelle direction ou autour de quels axes les masses agissent lors de la détermination des valeurs propres. Les masses peuvent agir dans les directions de déplacement global X, Y ou Z ainsi que tourner autour des axes X, Y et Z. Cochez les cases correspondantes. Au moins une direction ou un axe doit être activé pour que les valeurs propres puissent être calculées.

Options

La dernière section de l'onglet « Général » offre une option de paramétrage importante pour l'analyse modale.

Chercher les fréquences propres au-delà de

Si des barres ou des surfaces individuelles dans le modèle ont une fréquence propre très faible, elles apparaissent d'abord comme des modes propres locaux. Si vous cochez la case, vous ne pouvez calculer que les valeurs propres supérieures à une certaine valeur « f » de la fréquence propre. Le nombre de résultats peut ainsi être réduit et limité aux valeurs propres pertinentes pour le modèle global.

Paramètres

L'onglet Paramètres permet de gérer d'autres paramètres pour l'analyse modale ainsi que les paramètres de calcul élémentaires.

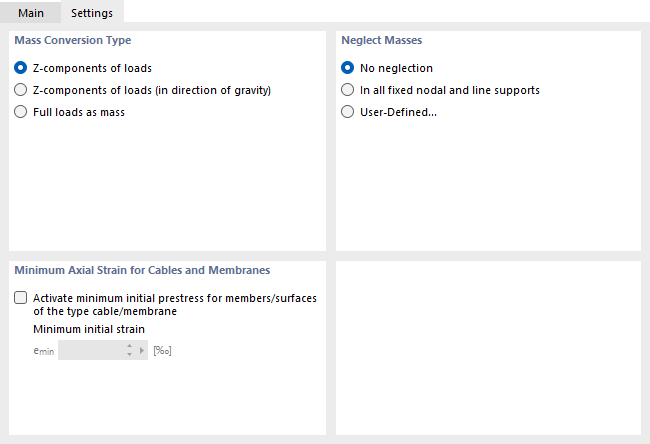
Type de conversion de masse

Cette section règle l'importation des masses pour l'analyse modale. Par défaut, seules les « Composantes en Z des charges » sont prises en compte. Il s'agit des composants de charge qui agissent dans les deux directions de l'axe Z - positive et négative.

Avec l'option « Composantes en Z des charges (dans le sens de gravité) », le programme n'applique que les composantes de charge efficaces dans la direction de la gravité. La gravité est déterminée par l'orientation de l'axe Z global (voir le chapitre Orientation des axes du manuel RFEM) : Elle agit en direction de l'axe Z global lorsqu'il est dirigé vers le bas. Si l'axe Z global est toujours aligné en haut, il agit dans la direction opposée

Avec l'option « Toutes les charges comme masse », toutes les charges sont importées et appliquées avec tous les composants comme masses.

Négliger les masses

Dans l'analyse modale, toutes les masses définies pour un modèle sont prises en compte. Cette section vous permet de négliger la masse de certaines parties du modèle, par exemple la masse de tous les appuis nodaux et linéiques encastrés. Vous pouvez également effectuer des sélections d'objets personnalisées.

Avec l'option « Défini par l'utilisateur », l'onglet supplémentaire « Négliger les masses » apparaît. Vous pouvez y spécifier les objets sans masse.

Vous pouvez créer la liste des objets (nœuds, lignes, barres, etc.) à l'aide des numéros d'objet. Vous pouvez également utiliser le bouton dans le champ de la « Liste d'objets » pour sélectionner graphiquement les objets. Le bouton permet de définir uniquement des appuis encastrés.

Déterminez dans quelle direction les masses doivent être négligées à l'aides des cases à cocher pour les directions de déplacement u_x, u_y, et u_z ainsi que les rotations φ_x, φ_z, et φ_z.

La rigidité des objets dont les masses sont négligées est néanmoins prise en compte dans la matrice. Si vous souhaitez négliger la rigidité de ces objets, vous pouvez utiliser une Modification de la structure pour ajuster la rigidité individuellement. Vous pouvez également désactiver les objets pour le calcul (voir le chapitre Général du manuel RFEM).

Déformation normale minimum pour les câbles et membranes

Pour entrer le câbles et membranes une déformation normale minimum est requise. Si la limite est trop basse, les valeurs propres atteintes ne sont pas réalistes et seuls les modes propres locaux sont déterminés. La valeur de précontrainte initiale par défaut pour e_min est appropriée dans la plupart des cas.