Configuração de análise modal

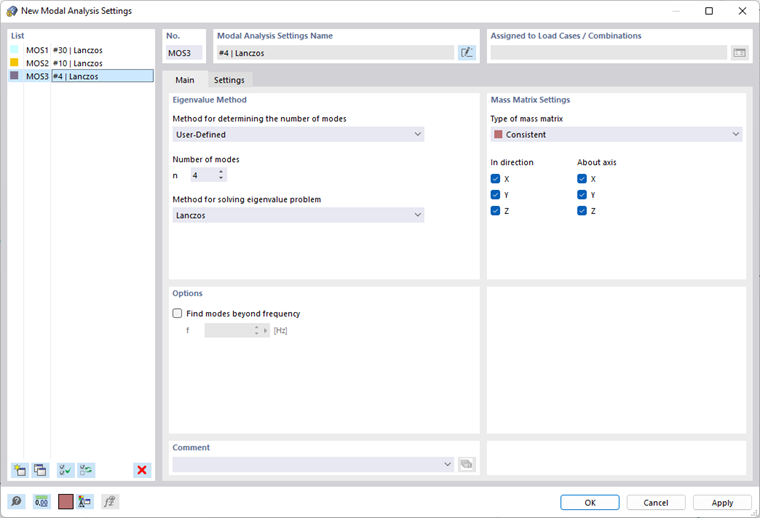
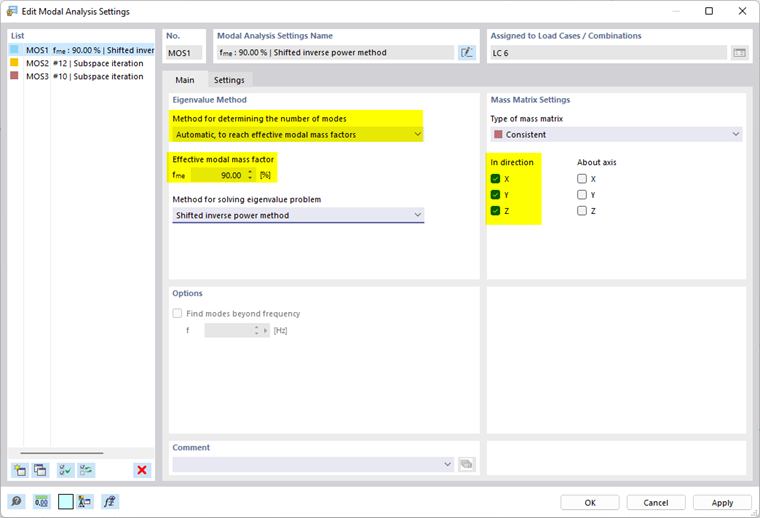
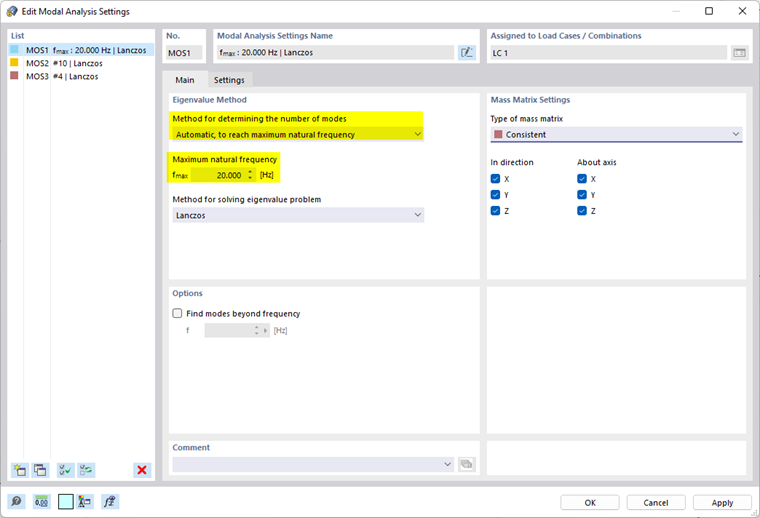
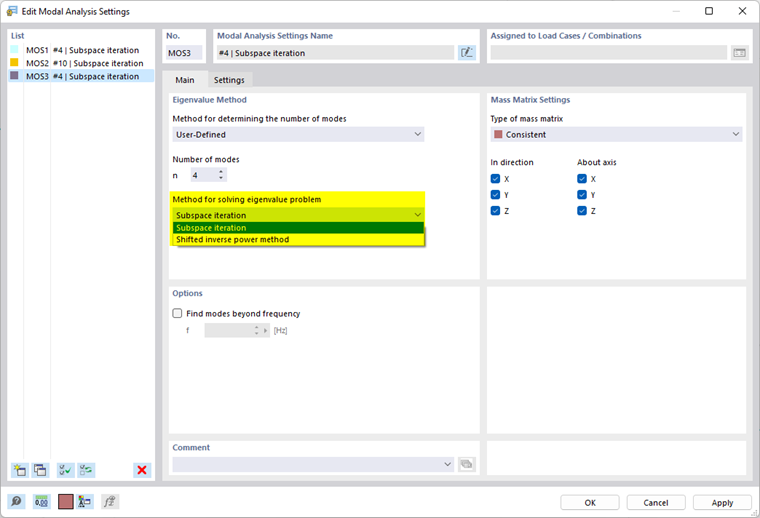
Uma configuração de análise modal ( MOS ) especifica as regras segundo as quais os valores próprios são calculados. Estão predefinidos dois tipos de análise padrão. Pode ajustar estes tipos ou criar outras configurações de análise modal a qualquer momento.

Geral

O separador Geral gere as configurações necessárias para a análise modal, bem como alguns outros parâmetros de cálculo elementos. O RFEM e o RSTAB oferecem diferentes opções para selecionar o método dos valores próprios.

Método dos valores próprios

Nesta secção, pode definir o método que é utilizado para analisar o problema de valores próprios e quantas formas próprias são determinadas.

Método para a determinação do número de formas

Pode seleccionar a partir de três opções na lista.

• Definido pelo utilizador

O método definido pelo utilizador permite especificar o número dos menores modos a serem calculados. É possível definir até 9999 formas próprias. Além deste limite, o modelo também representa uma restrição no número de formas próprias possíveis: Corresponde aos graus de liberdade resultantes do número de pontos de massa livres multiplicado pelo número de direções nas quais as massas atuam.

• Automático, para atingir os fatores de massa modal efetivos

O programa determina quantos modos próprios forem necessários até ser atingido o fator de massa modal especificado. Os fatores de massa modal efetivos são analisados para as direções translacionais especificadas (X, Y, Z).

• Automático, para atingir a frequência natural máxima

O programa determina quantos modos próprios forem necessários até ser atingida a frequência natural especificada.

Método para resolver problemas de valores próprios (para o RFEM)

Na lista, estão disponíveis três métodos para resolver o problema de valores próprios. Se tiver definido o método automático para determinar o número de valores próprios, apenas está disponível um método de resolução.

Para mais informações sobre os métodos individuais, ver Bathe {%>

• Lanczos

O método de Lanczos é adequado como método iterativo para determinar os valores próprios mais baixos e as formas próprias correspondentes de modelos grandes. Na maioria dos casos, este algoritmo permite atingir uma convergência rápida. É possível calcular até n–1 formas próprias ( n : graus de liberdade do modelo com massa).

Pode encontrar uma descrição introdutória em pt.wikipedia.org/wiki/Lanczos_algorithm.

• Raiz de polinomial característico

Com este método, a solução analítica de um problema de valores próprios é realizada através de um método direto. A principal vantagem deste método é a precisão dos valores próprios mais elevados e o facto de todos os valores próprios do modelo poderem ser determinados. Para modelos maiores, este método pode ser bastante demorado.

Pode encontrar uma descrição introdutória em https://en.wikipedia.org/wiki/Características-polynomialpt.wikipedia.org/wiki/Características-polynomial.

• Iteração do subespaço

Com este método, todos os valores próprios são determinados num único passo. Neste caso, o espectro da matriz de rigidez tem uma forte influência na duração do cálculo. Portanto, este método apenas é recomendado para modelos de EF grandes, se pretende calcular poucos valores próprios. A memória de trabalho limita o número de valores próprios que podem ser determinados num período de tempo razoável.

Pode encontrar uma descrição introdutória em pt.wikipedia.org/wiki/Krylov_subspace.

Método para resolver problema de valores próprios (para RSTAB)

Na lista, encontram-se disponíveis dois métodos para resolver o problema de valores próprios. Se tiver especificado um dos métodos automáticos para determinar o número de valores próprios, apenas está disponível um método de resolução.

Para mais informações sobre os métodos individuais, ver Bathe {%>

• Iteração do subespaço

Com este método, todos os valores próprios são determinados num único passo. Neste caso, o espectro da matriz de rigidez tem uma forte influência na duração do cálculo. Portanto, este método apenas é recomendado para modelos de EF grandes, se pretende calcular poucos valores próprios. A memória de trabalho limita o número de valores próprios que podem ser determinados num período de tempo razoável.

Pode encontrar uma descrição introdutória em pt.wikipedia.org/wiki/Krylov_subspace.

• Método das potências invertidas deslocadas

O método baseia-se em suposições para as formas próprias das formas próprias, as quais são aproximadas iterativamente para uma solução convergente durante o cálculo. A vantagem deste método é o tempo de cálculo curto devido à convergência rápida. O "Shift" significa que este método também pode ser utilizado para determinar todos os resultados entre o maior e o menor dos valores próprios de uma matriz dada.

Pode encontrar uma descrição introdutória em pt.wikipedia.org/wiki/Inversa_iteration.

Configuração da matriz de massas

Nesta secção de diálogo, pode definir qual a matriz de massa é utilizada e em torno de que eixos as massas devem actuar na análise modal.

tipo de matriz de massa

Estão disponíveis três tipos de matrizes de massa para seleção na lista.

• Diagonal

No caso da matriz diagonal de massas M, assume-se que as massas estão concentradas nos nós de EF. A entrada na matriz são as massas concentradas nas direções de translação X, Y e Z, bem como nas direções de rotação em torno dos eixos globais X (φ_X ), Y (φ_Y ) e Z (φ_Z ). É necessário distinguir os dois casos seguintes:

– Matriz diagonal só com graus de liberdade de translação: Se apenas as direções de translação forem ativadas para a matriz diagonal, a matriz diagonal resulta em:

– Matriz diagonal com graus de liberdade de translação e rotação: Se as direções de translação e rotação forem ativadas, a matriz diagonal resulta em:

• Consistente

A matriz de massa consistente é uma matriz de massa completa de elementos finitos. Portanto, as massas não estão concentradas no nó de EF. Em vez disso, as funções de forma são utilizadas para uma distribuição mais realista das massas dentro dos elementos finitos. Utilizando esta matriz de massa, são consideradas as entradas não diagonais na matriz, de modo que a rotação das massas geralmente é tida em consideração. A matriz de massa consistente é estruturada da seguinte forma (as funções de forma são negligenciadas por razões de simplicidade):

• unidade

A matriz de unidade substitui todas as massas definidas anteriormente. Esta matriz é uma matriz consistente onde todos os elementos da diagonal são de 1 kg. A massa é definida como 1 em cada nó de EF. As translações e rotações das massas são consideradas. Esta abordagem matemática deve ser utilizada apenas para análises numéricas.

Mais informação sobre os tipos de matriz e especialmente sobre a utilização da matriz unitária pode ser encontrada em Barth/Rustler {%>

Na direção/Em torno do eixo

Seis caixas de selecção controlam em que direcção ou em torno de que eixo as massas actuam quando determinam os valores próprios. As massas podem actuar nas direções de deslocamento global X, Y ou Z e rodar em torno dos eixos X, Y e Z. Selecione as caixas de seleção relevantes. É necessário ativar pelo menos uma direção ou um eixo para calcular os valores próprios.

Opções

A última secção de diálogo no separador "Geral" oferece uma importante opção de configuração para a análise modal.

Localizar modelos além da frequência

Se as barras ou superfícies individuais no modelo tiverem uma frequência natural muito baixa, estas ocorrem primeiro como formas próprias locais. Se seleciona a caixa de seleção, apenas os valores próprios acima de um determinado valor "f" da frequência natural serão calculados. Desta forma, pode reduzir o número de resultados e limitar os valores próprios que são relevantes para o modelo global.

configuracao

O separador Configurações gere as configurações adicionais necessárias para a análise modal, bem como os parâmetros de cálculo básicos.

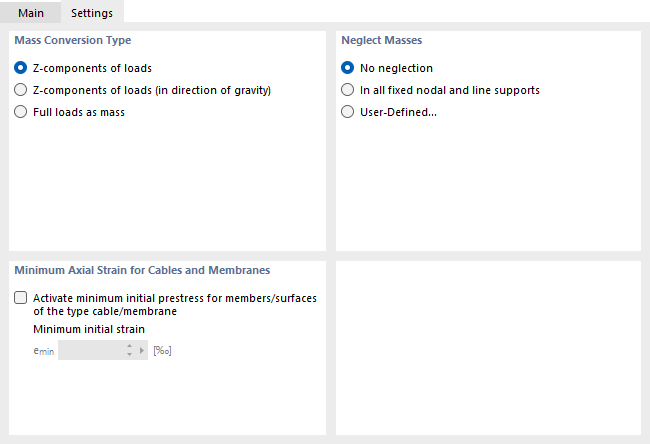
tipo de conversão de massa

Esta secção de diálogo controla a importação das massas para a análise modal. Por defeito, apenas os "'componentes Z das cargas" são tidos em consideração. Isto refere-se aos componentes da carga que atuam em ambas as direções do eixo Z, positiva e negativa.

Com a opção "Componentes de carga em Z (na direção da gravidade)", o programa aplica apenas os componentes de carga que são efetivos na direção da gravidade. A gravidade é determinada pela orientação do eixo global Z (ver capítulo {%>

Selecione a opção "Cargas totais como massa" para importar todas as cargas e aplicar todos os componentes como massas.

Negligenciar massas

A análise modal tem em consideração todas as massas definidas num modelo. Esta secção de diálogo inclui a opção para negligenciar a massa das partes do modelo, tais como a massa em todos os apoios fixos de nós e linhas. Também pode efetuar uma seleção de objetos definida pelo utilizador.

Ao selecionar a opção "Definido pelo utilizador", aparece o separador adicional "Negligenciar massas". Aqui pode especificar os objectos sem massas.

A lista de objetos (nós, linhas, barras etc.) pode ser criada diretamente através dos números dos objetos. Como alternativa, pode utilizar o Botão na caixa de texto da "Lista de objetos" para selecionar os objetos graficamente. Clique no botão apenas para apoios fixos predefinidos.

Utilize as caixas de seleção para as direções de deslocamento u_X, u_Y e u_Z, bem como para as rotações φ_X, φ_Y e φ_Z para definir em que direção as massas devem ser negligenciadas.

A rigidez dos objectos cujas massas são negligenciadas é, contudo, considerada na matriz. Se também pretende negligenciar a rigidez desses objetos, pode utilizar a Modificação da estrutura para ajustar a rigidez individualmente. Também é possível desativar os objetos para o cálculo (ver capítulo Main do manual do RFEM).

Deformação axial mínima para cabos e membranas

A entrada correta de barras de cabo e superfícies de membrana requer uma alteração mínima no comprimento. Se o limite definido é muito baixo, os valores próprios alcançados não são realistas e apenas são determinados os modos próprios locais. O valor padrão do pré-esforço inicial para_emin é adequado na maioria dos casos.