Una configuración de análisis modal ( MOS ) especifica las reglas según las cuales se calculan los valores propios. Se preestablecen dos tipos de análisis estándar. Puede ajustar estos tipos o crear más configuraciones de análisis modal en cualquier momento.
Datos básicos
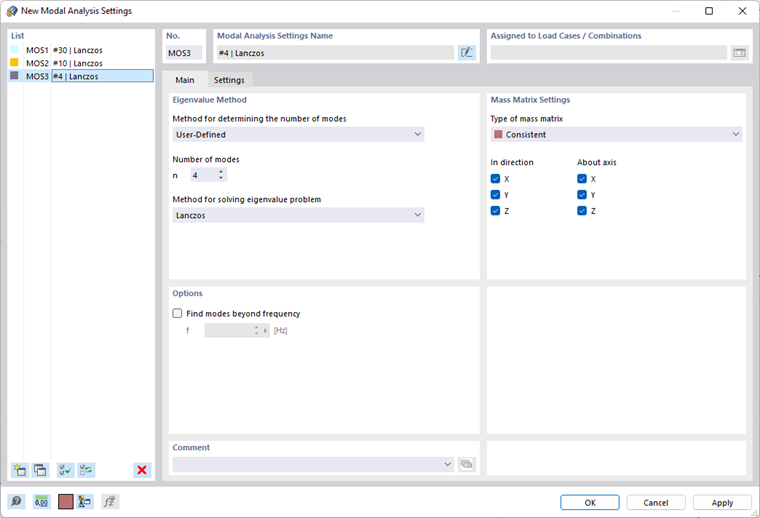
La pestaña Principal gestiona la configuración necesaria para el análisis modal, así como algunos otros parámetros de cálculo elementales. RFEM y RSTAB ofrecen diferentes opciones para seleccionar el método de los valores propios.
Método de valores propios
En esta sección, puede definir qué método se usa para analizar el problema de valores propios y cuántas deformadas del modo se determinan.
Método determinativo de número de modos
Puede seleccionar entre tres opciones en la lista.
- Definido por el usuario
El método definido por el usuario le permite especificar el número de los modos más pequeños que se van a calcular. Es posible definir hasta 9.999 deformadas del modo. Además de este límite, el modelo también representa una restricción en el número de deformadas del modo posibles: Corresponde a los grados de libertad que resultan del número de puntos de masa libre multiplicados por el número de direcciones en las que actúan las masas.
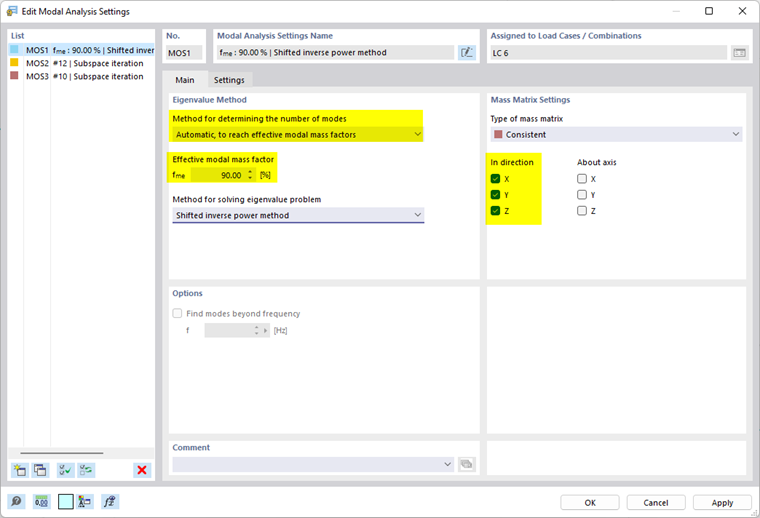
- Automáticamente para obtener factores de masa modal eficaces
El programa determina tantos modos propios como sea necesario hasta que se alcance el factor de masa modal especificado. Los factores de masa modal eficaz se analizan para las direcciones de traslación especificadas (X, Y, Z).
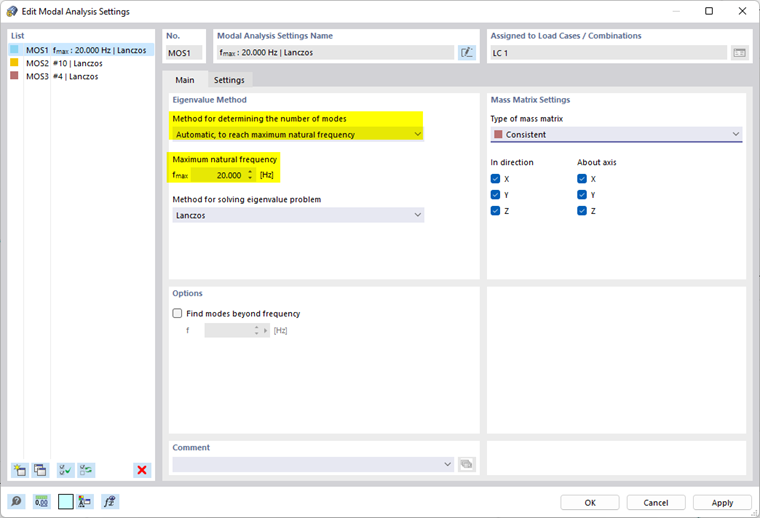
- Automáticamente para obtener la frecuencia natural máxima
El programa determina tantos modos propios como sea necesario hasta que se alcance la frecuencia natural especificada.
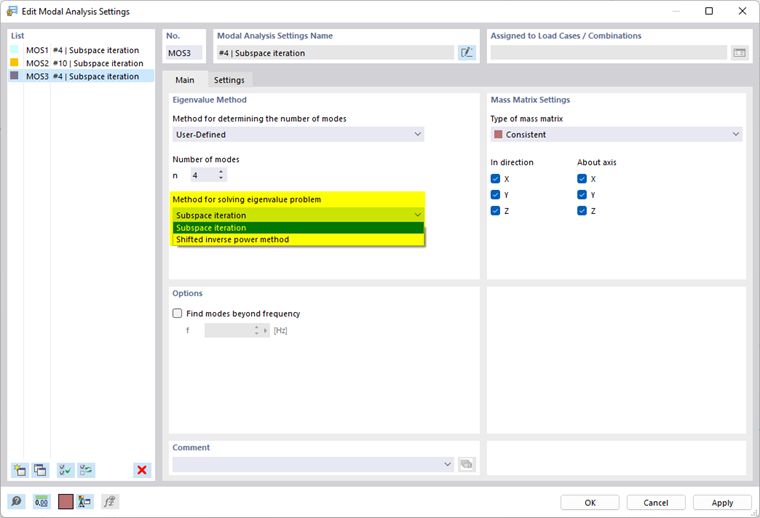
Método para resolver el problema de valores propios (para RFEM)
En la lista, hay tres métodos disponibles para resolver el problema de valores propios. Si ha establecido el método automático para determinar el número de valores propios, solo está disponible un método de resolución.
Para obtener más información sobre los métodos individuales, consulte Bathe [1] y Natke [2].
- Lanczos
El método de Lanczos es adecuado como método iterativo para determinar los valores propios más bajos y las deformadas del modo correspondientes de modelos grandes. En la mayoría de los casos, este algoritmo permite alcanzar una convergencia rápida. Es posible calcular hasta n–1 deformadas del modo ( n : grados de libertad del modelo con masa).
Se puede encontrar una descripción introductoria en es.wikipedia.org/wiki/Lanczos_algorithm.
- Raíz del polinomio característico
Con este método, la solución analítica de un problema de valores propios se lleva a cabo en un método directo. La principal ventaja de este método es la precisión de los valores propios más altos y el hecho de que se pueden determinar todos los valores propios del modelo. Para modelos más grandes, este método puede llevar bastante tiempo.
Se puede encontrar una descripción introductoria en es.wikipedia.org/wiki/Polinomio_característico.
- Iteración en el subespacio
Con este método, todos los valores propios se determinan en un solo paso. Con este método, el ancho de banda de la matriz de rigidez tiene una gran influencia en el tiempo de cálculo. Por lo tanto, este método solo se recomienda para modelos de EF grandes si desea calcular algunos valores propios. La memoria de trabajo limita el número de valores propios que se pueden determinar en un tiempo razonable.
Se puede encontrar una descripción introductoria en de.wikipedia.org/wiki/Krylow-Unterraum-Verfahren (en alemán).
Método para resolver el problema de valores propios (para RSTAB)
En la lista, hay dos métodos disponibles para resolver el problema de valores propios. Si ha especificado uno de los métodos automáticos para determinar el número de valores propios, solo está disponible un método de resolución.
Para obtener más información sobre los métodos individuales, consulte Baño [1].
- Iteración en el subespacio
Con este método, todos los valores propios se determinan en un solo paso. Con este método, el ancho de banda de la matriz de rigidez tiene una gran influencia en el tiempo de cálculo. Por lo tanto, este método solo se recomienda para modelos de EF grandes si desea calcular algunos valores propios. La memoria de trabajo limita el número de valores propios que se pueden determinar en un tiempo razonable.
Se puede encontrar una descripción introductoria en de.wikipedia.org/wiki/Krylow-Unterraum-Verfahren (en alemán).
- Método de la potencia inversa desplazada
Este método se basa en suposiciones para los vectores propios de las deformadas de los modos, que se aproximan iterativamente a una solución convergente durante el cálculo. La ventaja de este método es el corto tiempo de cálculo debido a la rápida convergencia. "Desplazamiento" significa que este método también se puede usar para determinar todos los resultados entre los valores propios más grandes y más pequeños de la matriz dada.
Se puede encontrar una descripción introductoria en de.wikipedia.org/wiki/Inverse_Iteration (en alemán).
Configuración de la matriz de masas
En esta sección del diálogo, puede definir qué matriz de masas se usa y en o sobre qué ejes deben actuar las masas en el análisis modal.
tipo de matriz de masas
Hay tres tipos de matrices de masas para elegir en la lista.
- Diagonal
En el caso de la matriz de masas diagonal M, se supone que las masas se concentran en los nudos de EF. Las entradas en la matriz son las masas concentradas en las direcciones de traslación X, Y y Z, así como las direcciones de giro alrededor de los ejes globales X (φX), Y (φY) y Z (φZ). Es necesario distinguir los dos casos siguientes:
– Matriz diagonal con solo grados de libertad traslacionales: Si solo se activan las direcciones de traslación para la matriz diagonal, la matriz diagonal da como resultado:
|
n |
Número de nudo de EF (1, 2...) |
|
j |
Direcciones X, Y y Z |
– Matriz diagonal con grados de libertad traslacionales y rotacionales: Si se activan las direcciones de traslación así como las direcciones de giro, la matriz diagonal da como resultado:
|
m |
Masa |
|
IX, IY, IZ |
Momentos de inercia de masas (RFEM 6) |
- Consistente
La matriz de masas diagonal es una matriz de masas completa de elementos finitos. Por lo tanto, las masas no se concentran en el nudo de EF. En su lugar, las funciones de forma se utilizan para una distribución más realista de las masas dentro de los elementos finitos. Usando esta matriz de masas, se consideran las entradas no diagonales en la matriz, de modo que generalmente se tiene en cuenta la rotación de las masas. La matriz de masas diagonal está estructurada de la siguiente manera (las funciones de forma se omiten en aras de la simplicidad):
- Unidad
La matriz unitaria sobrescribe todas las masas definidas previamente. Esta matriz es una matriz consistente donde todos los elementos diagonales son de 1 kg. La masa se establece en 1 en cada nudo de EF. Se tienen en cuenta las traslaciones y rotaciones de masas. Este enfoque matemático debe usarse solo para análisis numéricos.
Para obtener más información sobre los tipos de matrices y especialmente sobre el uso de la matriz identidad, consulte Barth/Rustler [3].
En dirección / respecto al eje
Seis casillas de verificación controlan en qué dirección o sobre qué ejes actúan las masas al determinar los valores propios. Las masas pueden actuar en las direcciones de desplazamiento global X, Y o Z, y girar sobre los ejes X, Y y Z. Seleccione las casillas de verificación relevantes. Es necesario activar al menos una dirección o eje para calcular los valores propios.
Opciones
La última sección del diálogo en la pestaña "Datos principales" proporciona una opción de configuración importante para el análisis modal.
Buscar modos propios por encima de su frecuencia
Si las barras o superficies individuales en el modelo tienen una frecuencia natural muy baja, se producen primero como modos propios locales. Si selecciona la casilla de verificación, solo se calcularán los valores propios por encima de un cierto valor "f" de la frecuencia natural. De esta manera, el número de resultados se puede reducir y restringir a los valores propios que son relevantes para el modelo entero.
Preferencias
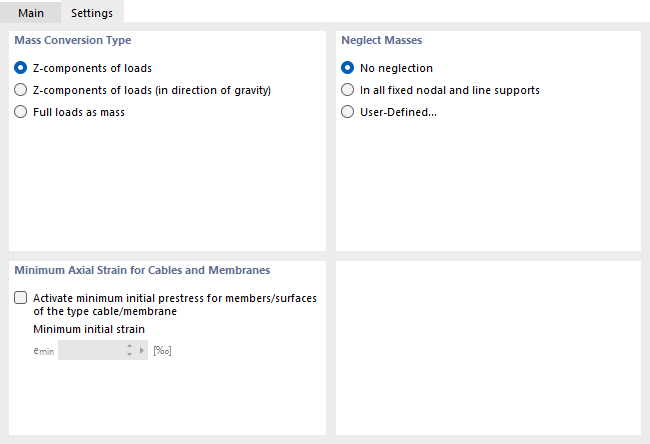
La pestaña Configuración gestiona la configuración adicional necesaria para el análisis modal, así como los parámetros de cálculo elementales.
Tipo de conversión de masas
Esta sección del diálogo controla la importación de masas para el análisis modal. De forma predeterminada, solo se tienen en cuenta los "'componentes Z de las cargas". Esto se refiere a los componentes de carga que actúan en ambas direcciones del eje Z, positiva y negativa.
Con la opción "Componentes de carga Z (en dirección de la gravedad)", el programa solo aplica los componentes de carga que son eficaces en la dirección de la gravedad. La gravedad está determinada por la orientación del eje Z global (consulte el capítulo Orientación de ejes del manual de RFEM): Actúa en la dirección del eje Z global si está orientado hacia abajo. Si el eje Z global está orientado hacia arriba, tiene el efecto contrario
Seleccione la opción "Cargas completas como masa" para importar todas las cargas y aplicar todos los componentes como masas.
Omitir masas
El análisis modal tiene en cuenta todas las masas definidas en un modelo. Esta sección del diálogo incluye la opción de omitir la masa de las partes del modelo, como la masa en todos los apoyos fijos en nudos y en línea. También puede realizar una selección de objetos definida por el usuario.
Al seleccionar la opción "Definido por el usuario", aparece la pestaña adicional "Omitir masas". Aquí puede especificar los objetos sin masas.
Puede crear directamente la lista de objetos (nudos, líneas, barras, etc.) utilizando los números de objeto. Como alternativa, utilice el
![]() en el cuadro de texto de la "Lista de objetos" para seleccionar los objetos gráficamente. Haga clic en el botón
en el cuadro de texto de la "Lista de objetos" para seleccionar los objetos gráficamente. Haga clic en el botón
![]() para preestablecer sólo apoyos fijos.
para preestablecer sólo apoyos fijos.
Utilice las casillas de verificación para las direcciones de desplazamientouX,uY yuZ, así como los girosφX,φY yφZ para definir en qué dirección se deben omitir las masas.
Sin embargo, la rigidez de los objetos cuyas masas se omiten se considera en la matriz. Si también desea omitir la rigidez de estos objetos, puede usar la Modificación estructural para ajustar las rigideces individualmente. También es posible desactivar los objetos para el cálculo (consulte el capítulo del manual de RFEM).
Mínima deformación axial para cables y membranas
La entrada correcta de y Superficies de membrana se requiere una deformación axial mínima. Si el límite se fija demasiado bajo, los valores propios alcanzados no son realistas y solo se determinan los modos propios locales. El valor predeterminado del pretensado inicial paraemin es adecuado en la mayoría de los casos.