The easiest way to do this is to use the add-on modules RF‑STABILITY (for RFEM 5) or RSBUCK (for RSTAB 8).
RF‑STABILITY and RSBUCK perform an eigenvalue analysis for the entire model with a certain state of the axial force. The axial forces are increased iteratively until the critical load case occurs. In the numerical analysis, the stability load is indicated by the fact that the determinant of the stiffness matrix becomes zero.
If the effective length factor is known, the buckling load and buckling mode are determined on this basis. For the lowest buckling load, all effective lengths and effective length factors are determined.
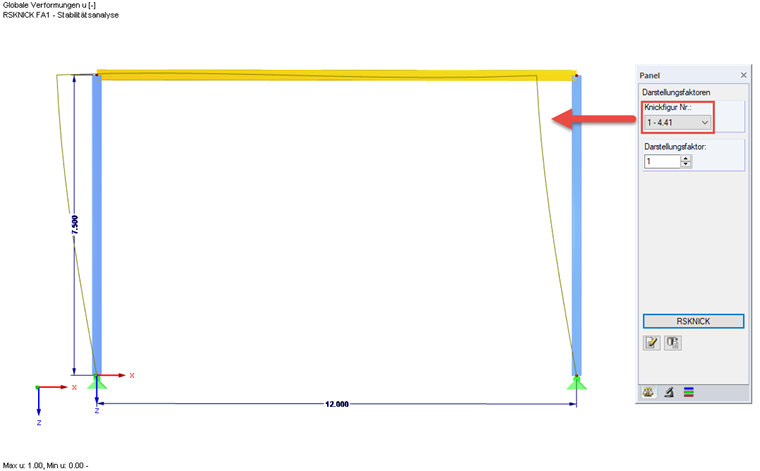
Depending on the required number of eigenvalues, the results show the critical load factors with the corresponding buckling curves, and the effective length about the major and the minor axis for each member, depending on the mode shape.
Since every load case usually has a different axial force state in the elements, a separate corresponding effective length result for the frame column is obtained for each load situation. The effective length whose buckling mode causes the column to buckle in the corresponding plane is the correct length for the design of the respective load situation.
Since this result may be different for each design due to the different load situations, the longest effective length of all calculated analyses is assumed as equal for all load situations.
Example for Manual Calculation and RF-STABILITY/RSBUCK
There is a 2D frame with a width of 12 m, a height of 7.5 m, and simple supports. The column cross-sections correspond to I240 and the frame beam to IPE 270. The columns are subjected to two different concentrated loads.
- l = 12 m
- h = 7.5 m
- E = 21,000 kN/cm²
- IyR = 5,790 cm4
- IyS = 4,250 cm4
- NL = 75 kN
- NR = 50 kN
This results in the following critical load factor:
The effective lengths of the frame columns can be determined as follows:
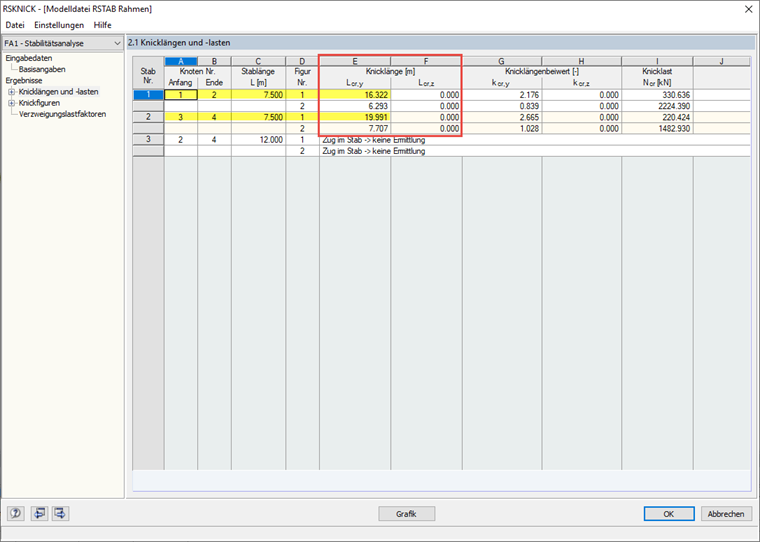
The results from the manual calculation correspond very well with those from RF‑STABILITY and RSBUCK.
RSBUCK
ηKi = 4.408
skL = 16.322 m
skR = 19.991 m
RF-STABILITY
ηKi = 4.408
skL = 16.324 m
skR = 19.993 m