Najłatwiej to zrobić, korzystając z modułów dodatkowych RF‑STABILITY (dla RFEM 5) lub RSBUCK (dla RSTAB 8).
RSKNICK und RF-STABIL führen eine Eigenwertanalyse für das Gesamtmodell mit einem bestimmten Normalkraftzustand durch. Die Normalkräfte werden iterativ so lange erhöht, bis der Verzweigungslastfall eintritt. Diese Stabilitätslast ist in der numerischen Berechnung dadurch gekennzeichnet, dass die Determinante der Steifigkeitsmatrix null wird.
Ist der kritische Lastfaktor bekannt, wird daraus die Knicklast und die Knickfigur ermittelt. Für diese niedrigste Knicklast werden dann die Knicklängen und Knicklängenbeiwerte bestimmt.
Als Ergebnis werden je nach geforderter Anzahl der Eigenwerte die kritischen Lastfaktoren mit den zugehörigen Knickfiguren und für jeden Stab je Eigenform eine Knicklänge um die starke und schwache Achse ausgegeben.
Da meist jeder Lastfall einen anderen Normalkraftzustand in den Elementen besitzt, ergibt sich für jede Lastsituation ein separates zugehöriges Knicklängenergebnis für die Rahmenstütze. Die Knicklänge, bei deren Knickfigur die Stütze in der entsprechenden Ebene wegknickt, ist die richtige Länge für den Nachweis der jeweiligen Lastsituation.
Da dieses Ergebnis aufgrund der verschiedenen Lastsituationen bei jeder Analyse unterschiedlich sein kann, nimmt man für einen Nachweis - auf der sicheren Seite liegend - die längste Knicklänge von allen berechneten Analysen gleich für alle Lastsituationen an.
Beispiel für Handrechnung und RSKNICK / RF-STABIL
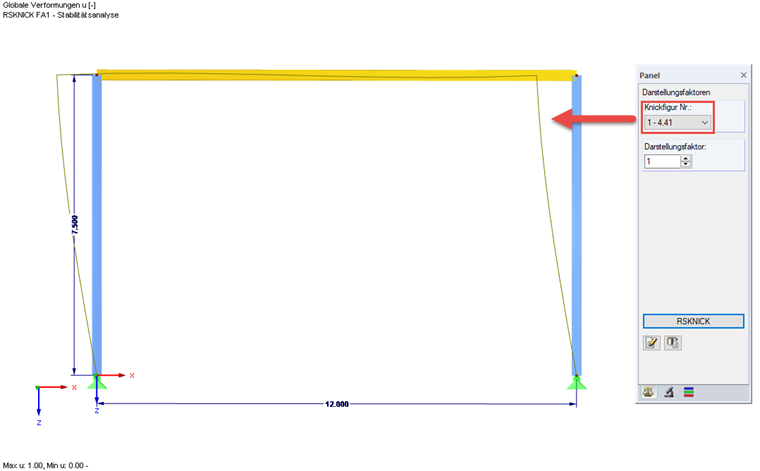
Gegeben ist ein 2D-Rahmen mit einer Breite von 12 m, einer Höhe von 7,5 m und gelenkigen Auflagern. Die Stützenquerschnitte entsprechen einem I240 und der Rahmenriegel einem IPE 270. Die Stützen werden mit zwei unterschiedlichen Einzellasten belastet.
- l= 12 m
- h= 7,5 m
- E= 21000 kN/cm²
- IyR = 5790 cm4
- IyS = 4250 cm4
- NL = 75 kN
- NR = 50 kN
Daraus ergibt sich folgender Verzweigungslastfaktor:
Die Knicklängen der Rahmenstützen können wie folgt ermittelt werden:
Die Ergebnisse aus der Handrechnung stimmen mit denen aus RSKNICK bzw. RF-STABIL sehr gut überein.
STABILITY (en)
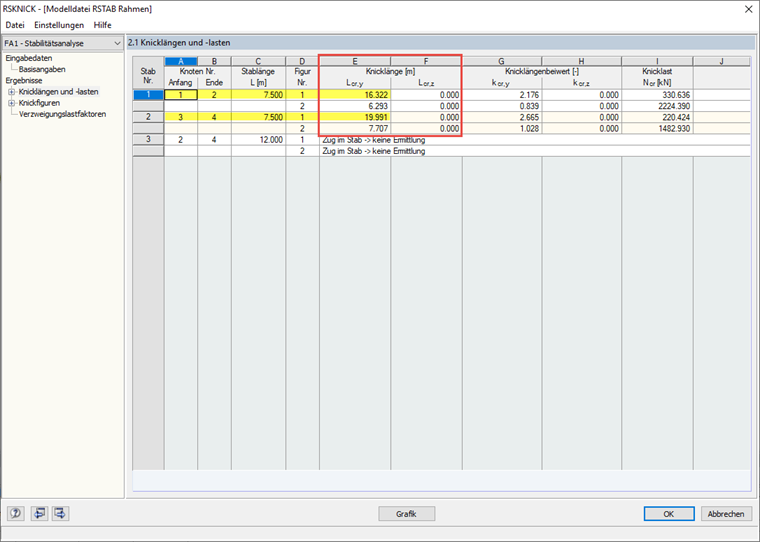
ηKi = 4.408
skL = 16.322 m
skR = 19.991 m
RF-STABILITY (en)
ηKi = 4.408
skL = 16.324 m
skR = 19.993 m