Nejjednodušší je použít přídavné moduly RF-STABILITY (pro RFEM 5) nebo RSBUCK (pro RSTAB 8).
Přídavné moduly RSBUCK a RF-STABILITY provádějí analýzu vlastních čísel pro celý model s určitým stavem normálové síly. Normálové síly se iteračně zvyšují až do vzniku případu kritického zatížení. Toto kritické zatížení je charakterizováno v numerickém výpočtu determinantem tuhosti matice s nulovou hodnotou.
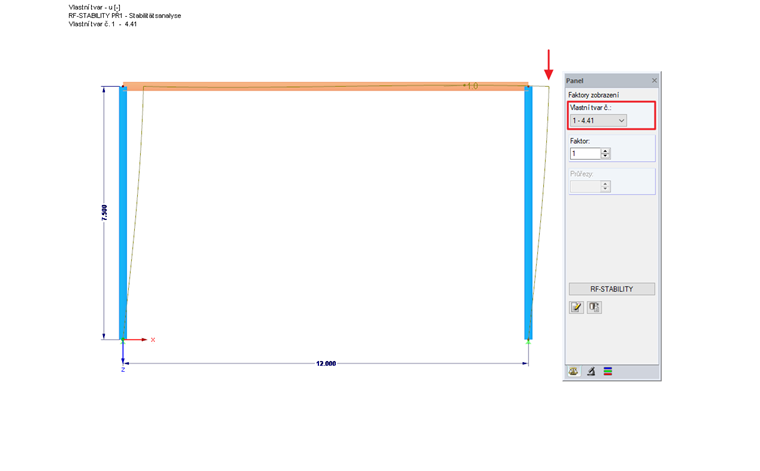
Pokud je znám součinitel kritického zatížení, stanoví se z něho kritická síla a tvar vybočení. Pro tuto nejmenší kritickou sílu se poté stanoví vzpěrné délky a součinitele vzpěrné délky.
V závislosti na požadovaném počtu vlastních čísel výsledky zobrazí součinitele kritického zatížení s odpovídajícími tvary vybočení a pro každý prut podle vlastního tvaru vzpěrnou délku okolo silné a slabé osy.
Jelikož každý zatěžovací stav obvykle má různý stav normálových sil v prvcích, vyplývá z toho pro každou zatěžovací situaci separátní příslušející výsledek vzpěrné délky pro sloup rámu. Účinná délka, při které sloup vybočí v příslušné rovině, je správnou délkou pro posouzení příslušné zatěžovací situace.
Vzhledem k tomu, že se výsledek může u různých posouzení u různých zatěžovacích situací lišit, přijímá se pro posouzení - ne straně bezpečnosti - nejdelší vzpěrná délka ze všech spočítaných posouzení stejná pro všechny zatěžovací situace.
Příklad ručního výpočtu a RSBUCK/RF-STABILITY
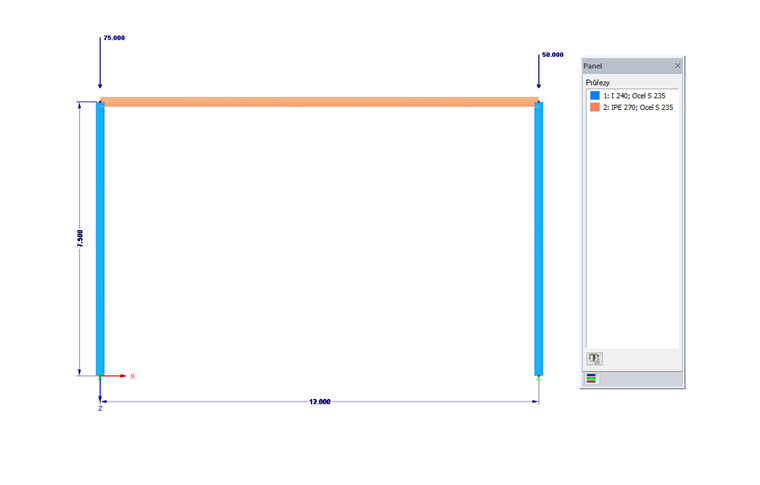
Je dán 2D rám o šířce 12 m, výšce 7,5 m a s kloubovými podporami. Průřezy sloupů odpovídají I240 a rámová příčel IPE 270. Sloupy se zatěžují pomocí dvou různých osamělých zatížení.
- l = 12 m
- h = 7,5 m
- E = 21000 kN/cm²
- IyR = 5790 cm4
- IyS = 4250 cm4
- NL= 75 kN
- NR= 50 kN
Výsledkem je následující součinitel kritického zatížení:
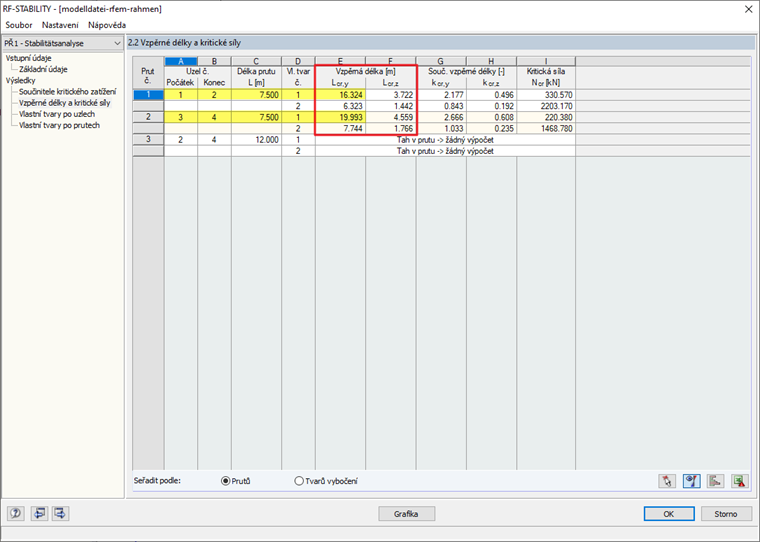
Vzpěrnou délku sloupů rámu je možné stanovit následovně:
Výsledky z ručního výpočtu dobře souhlasí s výsledky z přídavného modulu RSBUCK resp. RF-STABILITY.
RSBUCK
ηKi = 4.408
skL = 16.322 m
skR = 19.991 m
Stabilní
ηKi = 4.408
skL = 16.324 m
skR = 19.993 m