| p(h) | Hydrostatic pressure depending on the height of the fluid level |
| h | Height of the fluid level above the considered point |
| ρ | Density of the fluid |
| g | Gravity acceleration |
| p0 | Air pressure on the fluid surface |
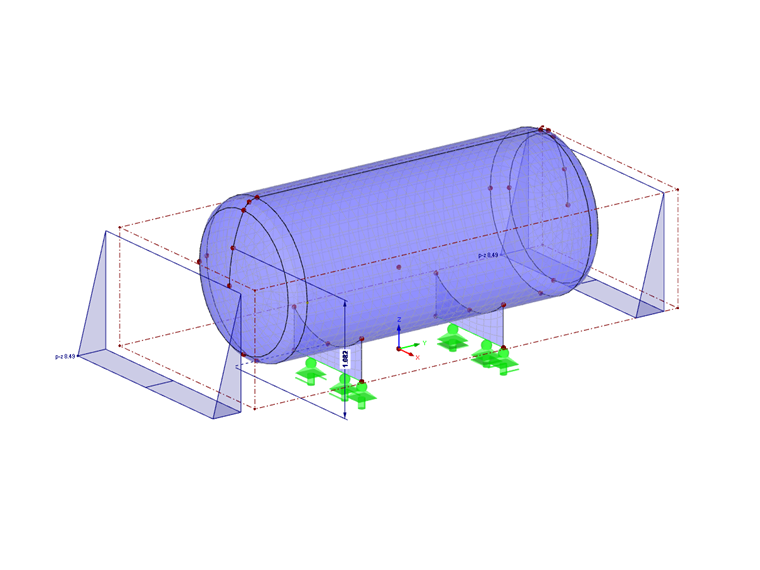
This loading can be simulated very efficiently in a load case in RFEM by means of the free rectangular loads.
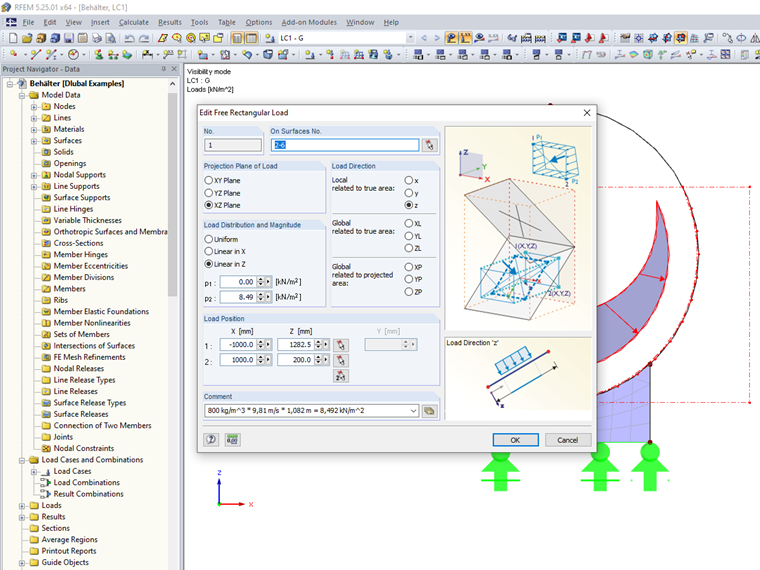
The free rectangular load is a surface load function for defining compressive loads on surfaces. The area of influence of this special load type is defined by a cuboid floating freely in space, which loads all assigned surfaces within the cuboid. Two points on a projection plane describe the side view, and the surface area of the assigned elements describes the length of the definition cuboid.
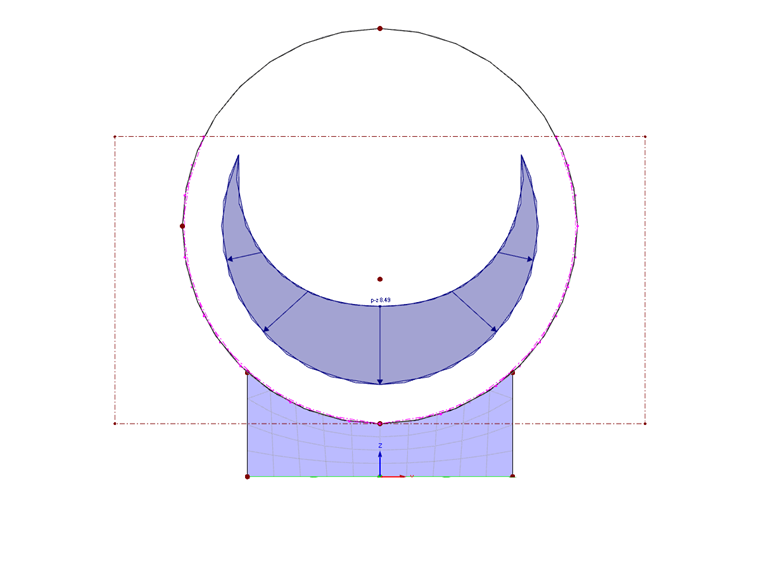
The simulation of a hydrostatic pressure requires that the pressure at each container point presses perpendicularly on the wall and increases linearly with the distance to the liquid level according to Pascal's law.
To achieve an effect perpendicular to the walls, select the load direction z "Local - related to true area". The linear distribution depending on the liquid level is achieved by switching to a linear load distribution in the respective direction and assigning the load ordinates at the definition points on the projection plane (zero above, value according to formula).
Tip: By changing the position of the upper definition Point p1 and the load ordinate at Point p2, different liquid levels can be simulated very quickly.
Knowledge Base