20x

2024-11-04

VE0065 | Dwuwarstwowy zbiornik grubościenny

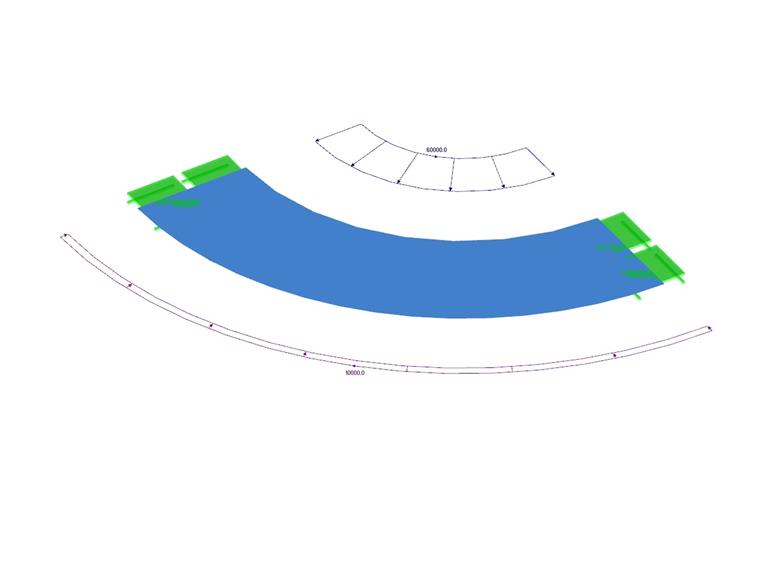
Opis prac

Dwuwarstwowe, grubościenne naczynie jest obciążone ciśnieniem wewnętrznym i zewnętrznym. Zbiornik jest otwarty, dlatego nie ma naprężenia osiowego. Problem jest zamodelowany jako ćwiartka. Określ ugięcie promieniowe promienia wewnętrznego i zewnętrznego u_r (r₁ ), u_r (r₂ ) oraz ciśnienie (naprężenie promieniowe) w środkowym promieniu p_m. Ciężar własny jest pomijany.

Materiał	Naczynie wewnętrzne	Moduł sprężystości	E₁	1,000	MPa
	Naczynie wewnętrzne	współczynnik Poissona	ν	0,250	-
	Naczynie zewnętrzne	Moduł sprężystości	E₂	0,500	MPa
	Naczynie zewnętrzne	współczynnik Poissona	ν	0,250	-
Geometria		Promień wewnętrzny	r₁	200.000	mm
		Środkowy promień	r_m	250.000	mm
		Promień zewnętrzny	r₂	300.000	mm
Obciążenie		Ciśnienie wewnętrzne	p₁	60.000	kPa
Obciążenie		Ciśnienie zewnętrzne	p₂	10.000	kPa

Dwuwarstwowy zbiornik grubościenny

Rozwiązanie analityczne

Rozwiązanie analityczne danego problemu jest analogiczne do rozwiązania analitycznego z VE0064 - Thick-Walled Vessel . Promieniowe ugięcie środkowego promienia naczynia wewnętrznego i zewnętrznego można obliczyć za pomocą następujących równań.

u_{r} (r_{m}) = \frac{r_{m}}{E_{1}} [K_{1} + \frac{C_{1}}{r_{m}^{2}} - ν (K_{1} - \frac{C_{1}}{r_{m}^{2}})]

u_{r} (r_{m}) = \frac{r_{m}}{E_{2}} [K_{2} + \frac{C_{2}}{r_{m}^{2}} - ν (K_{2} - \frac{C_{2}}{r_{m}^{2}})]

Ugięcie promieniowe środkowego promienia zbiornika wewnętrznego i zewnętrznego

Stałe K₁, C₁, K₂ i C₂ są obliczane kolejno dla każdego zbiornika na podstawie odpowiednich promieni i ciśnień granicznych. Korzystając z tych równań, można określić ciśnienie w powierzchni granicznej_pm.

p_{m} = \frac{2 (E_{1} p_{2} r_{2}^{2} (r_{1}^{2} - r_{m}^{2}) + E_{2} p_{1} r_{1}^{2} (r_{m}^{2} - r_{2}^{2}))}{E_{2} (r_{2}^{2} - r_{m}^{2}) ((1 + ν) r_{1}^{2} + (1 - ν) r_{m}^{2}) + E_{1} (r_{m}^{2} - r_{1}^{2}) ((1 + ν) r_{2}^{2} + (1 - ν) r_{m}^{2})}

Ciśnienie w granicy faz

Z kolei można obliczyć przemieszczenia promieniowe u_r (r₁ ), u_r (r₂ ).

u_{r} (r_{1}) = \frac{r_{1}}{E_{1}} (K_{1} + \frac{C_{1}}{r_{1}^{2}} - ν (K_{1} - \frac{C_{1}}{r_{1}^{2}}))

u_{r} (r_{2}) = \frac{r_{2}}{E_{2}} (K_{2} + \frac{C_{2}}{r_{2}^{2}} - ν (K_{2} - \frac{C_{2}}{r_{2}^{2}}))

Promieniowe przemieszczenie wewnętrznego i zewnętrznego promienia

Ustawienia RFEM

Modelowany w RFEM 5.06 i RFEM 6.06
Rozmiar elementu wynosi l_FE = 2.000 mm
Zastosowano izotropowy liniowo sprężysty model materiałowy

Wyniki

RFEM 6 Wyniki – Całkowite Ugięcie

Ilość	Rozwiązanie analityczne	RFEM 6	Stosunek	RFEM 5	Stosunek
p_m [kPa]	21.655	21.663	1,000	21.648	1,000
u_r (r₁ ) [mm]	33,605	33.602	1,000	33,605	1,000
u_r (r₂ ) [mm]	27.287	27.283	1,000	27.287	1,000

444x

Przykład weryfikacji 000065 | 1

;