1. příklad: Betonová deska na 9 vrtaných pilotách
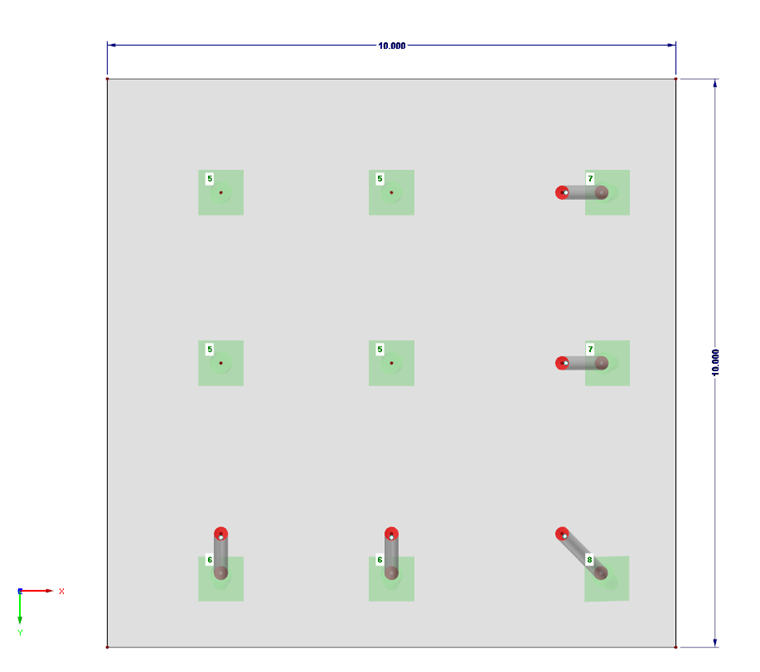
Betonová deska o rozměrech 10 x 10 m s tloušťkou 18 cm je podepřena 9 vrtanými pilotami, přičemž 4 z nich (uzlová podpora 5) včetně středové vrtané piloty přenášejí pouze síly ve směru Z. Dvě z ostatních vrtaných pilot vykazují sklon 10° vůči ose X (uzlová podpora 6), dvě další pak sklon 10° vůči ose Y (uzlová podpora 7) a jedna vrtaná pilota má sklon 10° vůči ose X i Y (uzlová podpora 8), takže se mohou přenášet vodorovné síly v příslušných směrech a konstrukce je stabilní.
Konstrukce je namáhána plošným zatížením 4,5 kN/m² a dále dvěma liniovými zatíženími, z nichž každé dosahuje 1,0 kN/m.
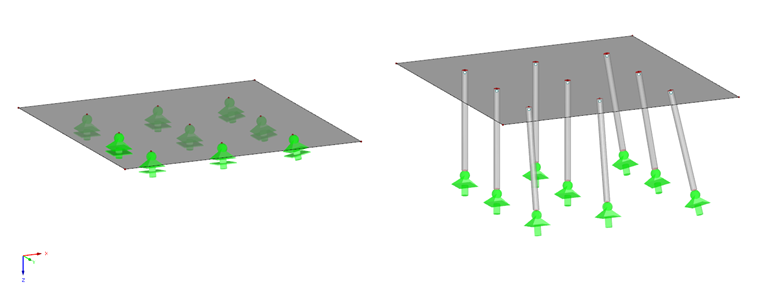
V první variantě modelujeme vrtané piloty jako přímé a nakloněné tuhé podpory, v druhé variantě pak jako kloubově připojené nosníky. Obě tyto varianty statického modelu se liší pouze v osové tuhosti nosníků.
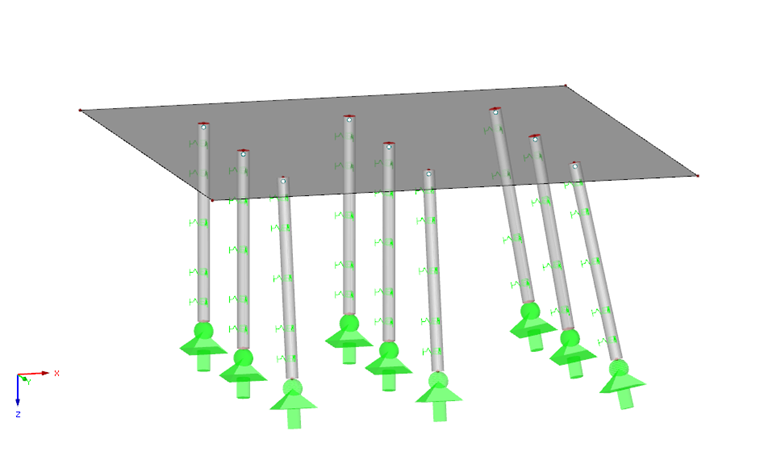
Třetí varianta odpovídá druhému řešení, je ovšem rozšířena o pružné uložení každého prutu v jeho lokálním směru y a z, kterým modelujeme poddajnost podloží.
Pro zadání konstant tuhosti viz článek Podloží prutu 1: Wegfedern und die FAQ Wie sind die Stabbettungen einzugeben? hingewiesen.
- KB 000489 | Podloží prutu 1: Translační tuhost
- FAQ | Zadání pružného podloží prutu pro vrtané piloty v programu RFEM
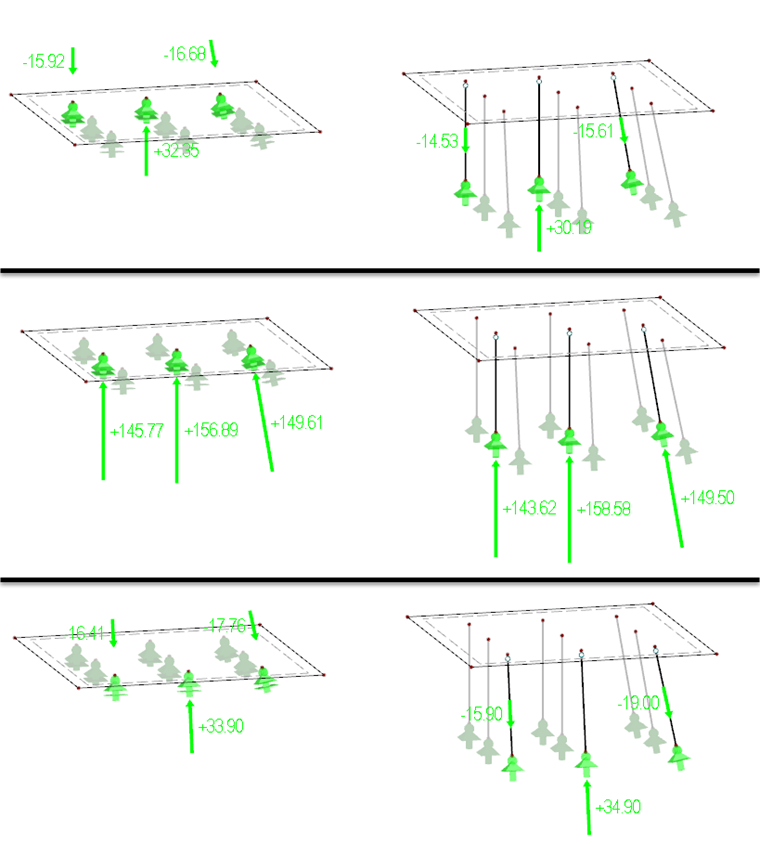
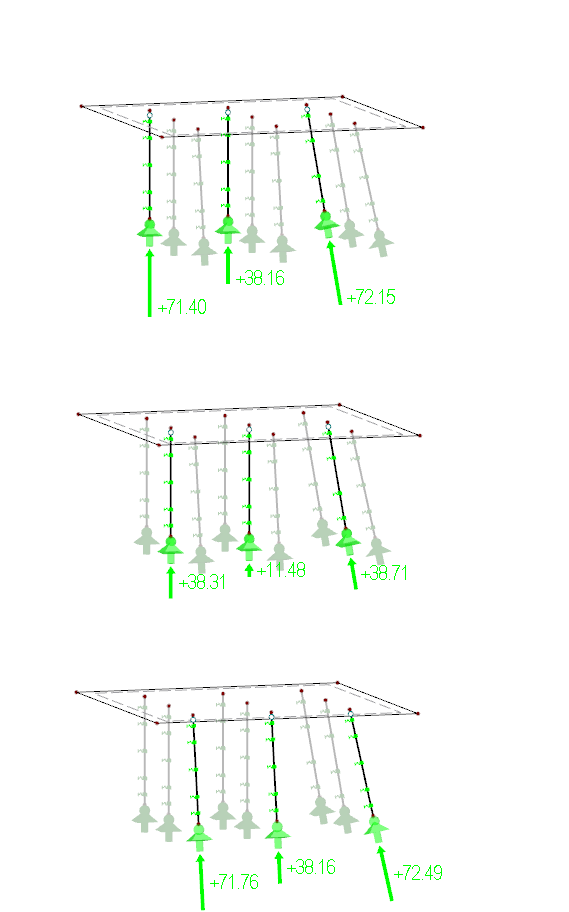
Rozdíly mezi těmito třemi variantami se projevují ve výsledcích. Jak jsme již uvedli výše, v podporových silách není u varianty 1 a 2 prakticky žádný rozdíl, proto si odpovídají také výsledky. Při zadaném zatížení vznikají v pilotách jak tahové, tak tlakové síly, přičemž rozdělení zatížení je poměrně nerovnoměrné a dosahuje vysokých hodnot. Co se týče maximální podporové síly, jsme u obou těchto variant na straně bezpečnosti. Na obr. 04 jsou zobrazeny v režimu viditelnosti podporové síly varianty 1 a 2 v jednotlivých řadách.
Pro redukci a rovnoměrnější rozložení podporových sil doporučujeme zadat pružné uložení prutů. Vznikají tak poměrně malé posouvající síly a ohybové momenty, takže v úvahu se budou brát pouze působící normálové síly, respektive podporové síly. Na obr. 05 si můžeme prohlédnout podporové síly varianty 3 opět po jednotlivých řadách v režimu viditelnosti.
2. příklad: Ocelová konstrukce na třech vrtaných pilotách
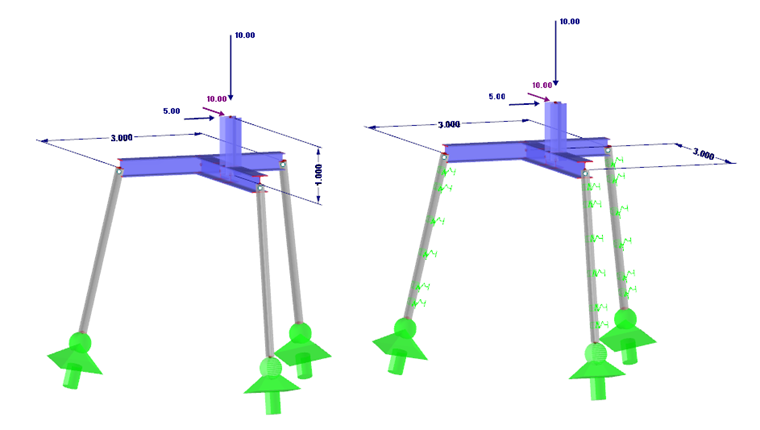
Ocelová konstrukce se skládá ze dvou 3 m dlouhých ocelových nosníků s ohybově tuhým spojením a jedné konzoly o délce 1 m. Konstrukce je na konci konzoly zatížena třemi osamělými břemeny ve všech třech směrech. Jako podepření slouží tři vrtané piloty se sklonem 10° vůči ose X, respektive Y.
An dieser Stelle werden zwei Modellierungsvarianten betrachtet: Variante 1 ohne Stabbettung, Variante 2 mit Stabbettung.
Při pohledu na statický systém jak v rovině XZ, tak YZ je okamžitě zřejmé, že konstrukce je nestabilní vzhledem k tomu, že směrnice sil působících ve vrtaných pilotách se protínají v jednom společném bodě.
Proto je zapotřebí definovat pružné podloží prutů.
Závěr a výhled
Bei der Modellierung von Bohrpfahlkonstruktionen liefern die prinzipiell beschriebenen zwei Möglichkeiten, sprich die Varianten mit oder ohne Stabbettung, unterschiedliche Ergebnisse. Pokud jde o normálové síly v pilotách, je varianta bez pružného podloží méně příznivá, zatímco zohlednění pružného podloží prutů je zpravidla hospodárnější. V případě nedostatečně vyztužených konstrukcí je nezbytné pružné podloží uvažovat, pokud je vyloučeno jiné vodorovné ztužení konstrukce.