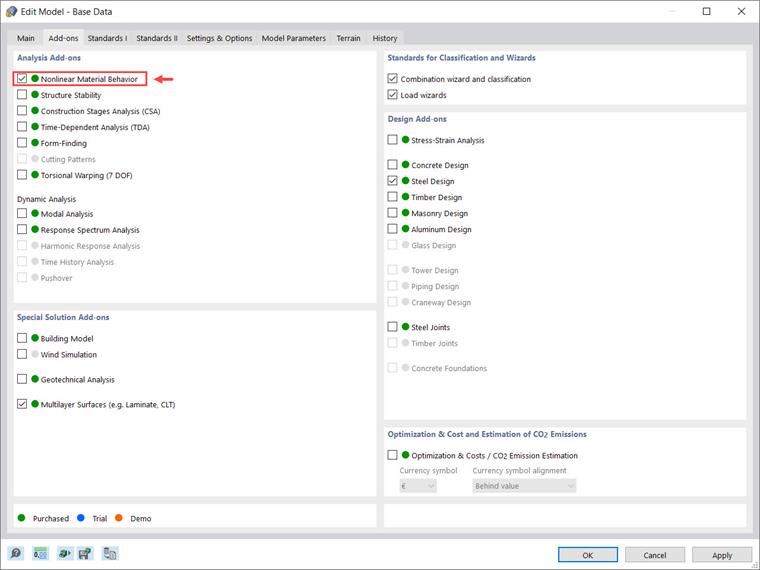
The Nonlinear Material Behavior add-on allows you to consider material nonlinearities in RFEM 6. You can activate this add-on in the Base Data of the model as shown in Image 1.
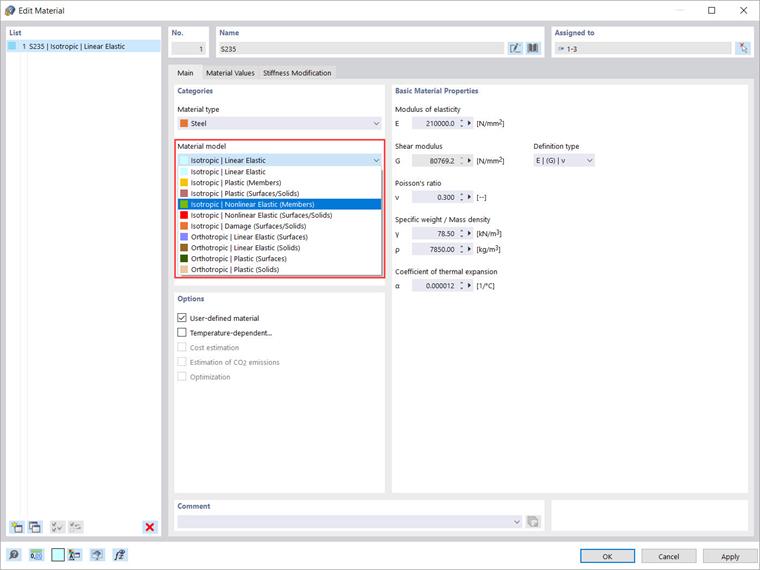
Once the Nonlinear Material Behavior analysis add-on is activated, in addition to the “Isotropic | Linear Elastic” and “Orthotropic | Linear Elastic” material models, further options are available for selection in the list (Image 2). You can, therefore, choose among the following material models:
- Isotropic | Plastic (Members)
- Isotropic | Plastic (Surfaces/Solids)
- Isotropic | Nonlinear Elastic (Members)
- Isotropic | Nonlinear Elastic (Surfaces/Solids)
- Isotropic | Damage (Surfaces/Solids)
- Orthotropic | Plastic (Surfaces)
- Orthotropic | Plastic (Solids)
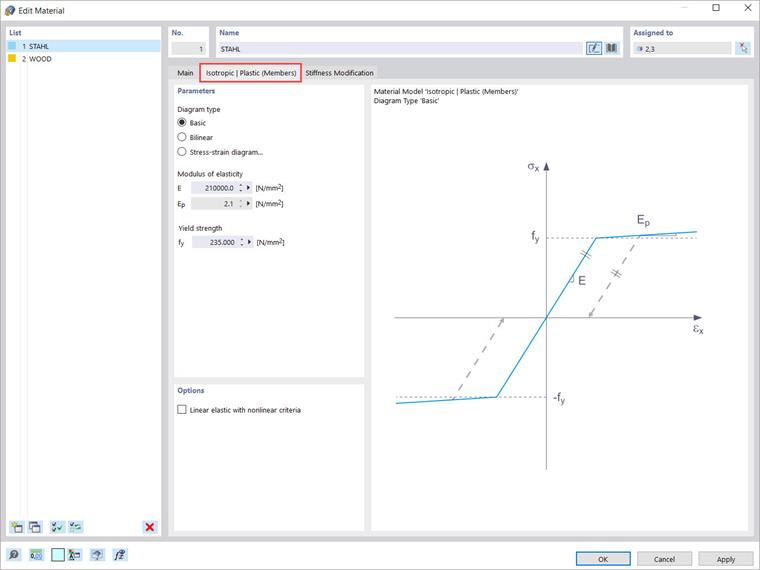
Isotropic | Plastic (Members) Material Model
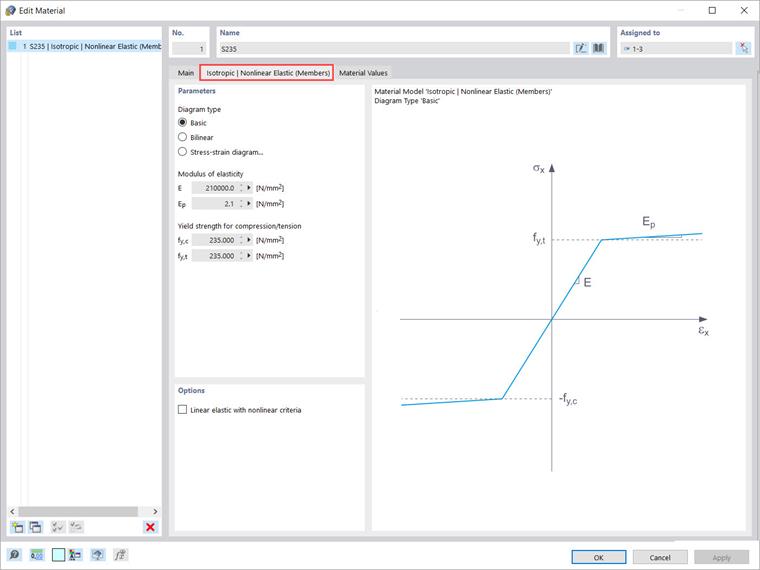
If you select one of the above entries in the "Material model" drop-down list, a new tab is available for entering the material parameters. Hence, by selecting the "Isotropic | Plastic (Members)” material model, a related tab appears as shown in Image 3.
First, you have the possibility to select the following options for the diagram type:
- Basic
- Bilinear
- Stress-strain diagram
If you select the first option (that is, “Basic”), the program uses values from the material database for the modulus of elasticity E and the yield strength fy. Please note that this is also a bilinear material model, where the branch of the graph is not exactly horizontal for numerical reasons and has a small Ep slope. In contrast, if the diagram is defined bilinearly (that is, the “Bilinear” option), the program allows you to enter the value of Ep yourself.
The third option available (that is, “Stress-strain diagram”) allows you to define more complex relations between stress and strain. Please note that in this material model the stress-strain diagram refers to the longitudinal stress σx. Different yield points for tension and compression cannot be taken into account by this option.
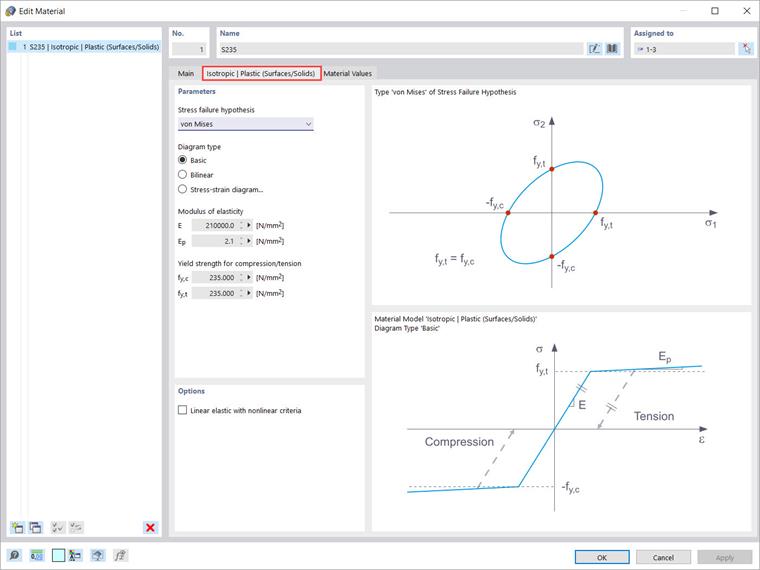
Isotropic | Plastic (Surfaces/Solids) Material Model
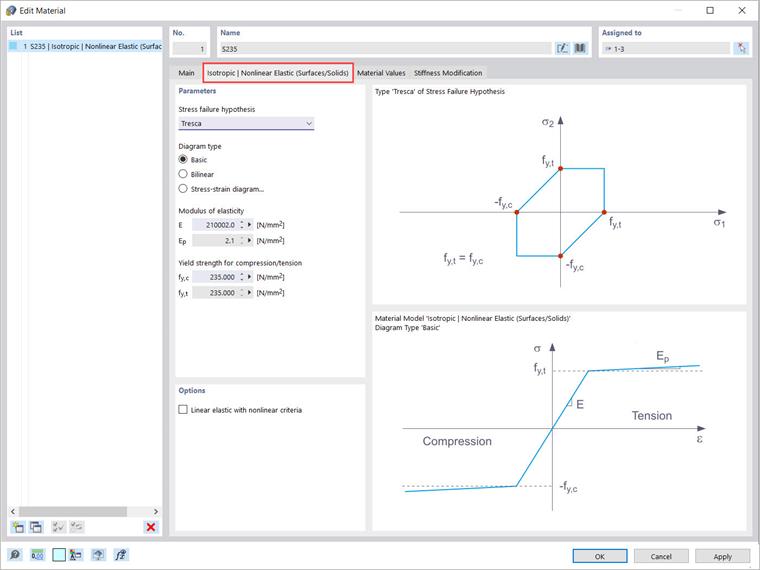
The isotropic plastic material model is also available for surfaces and solids. In the same way as for the “Isotropic | Plastic (Members)” model, a related tab appears when selecting the “Isotropic | Plastic (Surfaces/Solids)” entry in the drop-down list. In addition to the options for defining the diagram type (the same as for “Isotropic | Plastic (Members)”), the “Stress failure hypothesis” must be selected (Image 4).
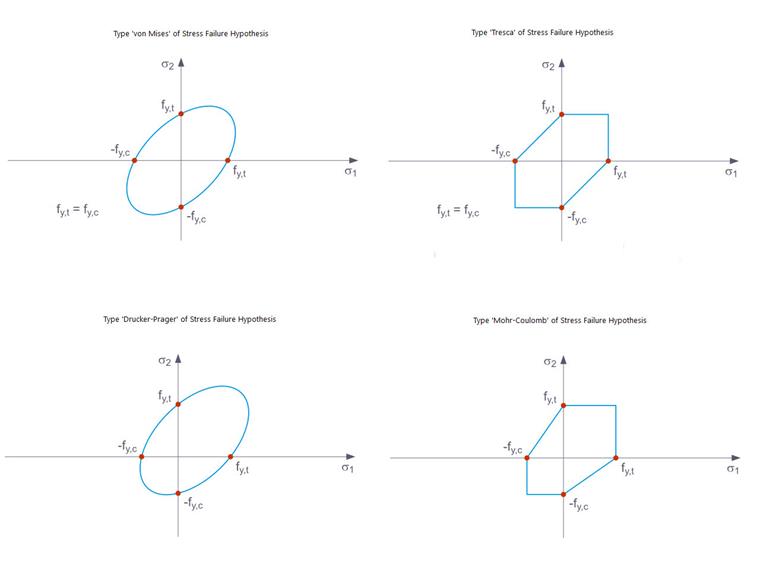
The following stress failure hypotheses are available for selection in the drop-down menu:
- von Mises
- Tresca
- Drucker-Prager
- Mohr-Coulomb
The yield criterion according to von Mises is a circular cylinder with a hydrostatic axis in the principal stress space. All stress states within this space are entirely elastic. Stress states outside this space are not allowed. With Tresca’s yield rule, the plastic yielding occurs due to the maximum shear stress.
As an extension of these yield criteria, there are the yield rules according to Drucker-Prager and Mohr-Coulomb, in which plastic yielding occurs when the maximum shear stress is locally exceeded. In the former there is a surface area with a smooth border in the principal stress space, while the latter is a surface area with a not smooth border (Image 5).
Isotropic | Nonlinear Elastic (Members) Material Model
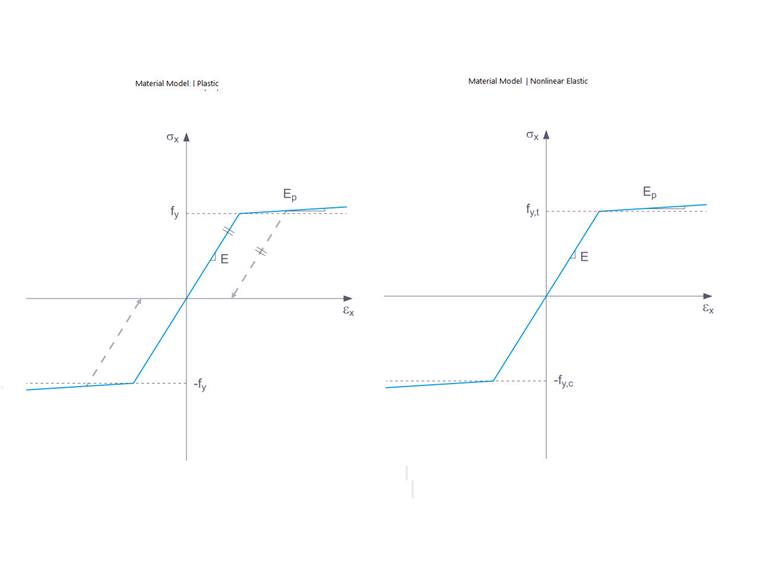
The tab for setting the parameters of the “Isotropic | Nonlinear Elastic (Members)” model is very similar to that of the “Isotropic | Plastic (Members)” material model (Image 6). In fact, these models correspond to each other. The difference between them is related to the general distinction between the nonlinear elastic materials models on one hand, and the plastic ones on the other hand.
If a structural component with a nonlinear elastic material is actually released again, the strain returns along the same path and there is no longer any strain when the component is completely unloaded. In the case of plastic materials, on the other hand, the strain remains even after the load has been fully relieved. This is shown graphically in Image 7.
Isotropic | Nonlinear Elastic (Surfaces/Solids) Material Model
The same discussion applies to the correspondence between the “Isotropic | Plastic (Surfaces/Solids)” and the “Isotropic | Nonlinear Elastic (Surfaces/Solids)” material models. The model’s properties should be defined in the same way (Image 8), with the difference that no plastic strain remains after the load has been removed.
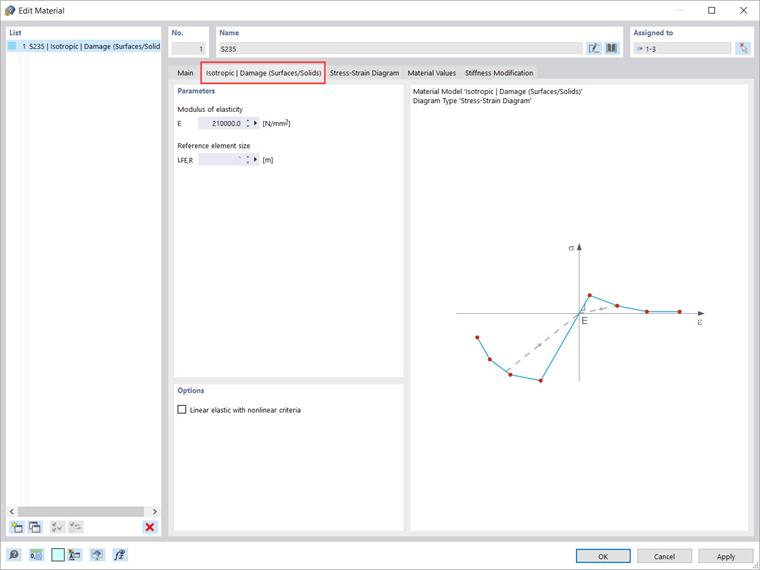
Isotropic | Damage (Surfaces/Solids) Material Model
The yield laws mentioned earlier in the article are restricted to the yield surface in the principal stress space, and their yield rules can only apply to purely elastic-plastic material behavior. However, many materials do not exhibit purely symmetric nonlinear behavior. In order to simulate the behavior of materials that are exposed to a damage process caused by cracks, a more suitable material model is required. One such material is concrete, which has a significantly higher compressive strength than tensile strength.
The cracks that occur in the tension area of the material reduce the rigidity of the system. In the case of reinforced concrete or reinforced fiber concrete, the reinforcement absorbs the tensile stresses.
To simulate the behavior of such materials (for example, steel fiber-reinforced concrete), RFEM 6 offers you the “Isotropic | Damage (Surfaces/Solids)” material model. If you select this material model, the tab shown in Image 9 is available to you for defining the model’s parameters.
Unlike other material models, the stress-strain diagram for this material model is not antimetric to the origin. The "Reference element size" controls how the strain in the crack area is scaled to the length of the element. With the default value zero, no scaling is performed. As a result, the material behavior of the steel fiber-reinforced concrete is modeled realistically.
Orthotropic | Plastic (Surfaces, Solids) | Tsai-Wu Material Model
With the orthotropic plastic material model for surfaces and solids in RFEM 6, surfaces and solids with plastic material properties can be calculated and evaluated according to the Tsai-Wu failure criterion. This material model combines plastic and orthotropic properties, which allows special modeling of materials with anisotropic properties. This material model can thus be used to represent the behavior of fiber-reinforced plastics or wood-based panels.
In this material model, the elastic range corresponds to the “Orthotropic | Linear Elastic (Solids)” material model, while for the plastic domain, yielding applies according to Tsai-Wu. Image 10 shows the yielding conditions for both surfaces (2D) and solids (3D).
If the value of fy(σ) according to the Tsai-Wu equation, plane stress state, is less than 1, the stresses are in the elastic range. The plastic domain is reached as soon as fy(σ) = 1. Values above 1 are not allowed. The model behavior is ideally plastic; that is, there is no stiffening.
Summary
The Nonlinear Material Behavior add-on enables the consideration of material non-linearities in RFEM 6. If you activate this add-on in the model’s Base Data, the list of material models expands and you can easily select the nonlinear material model of interest.
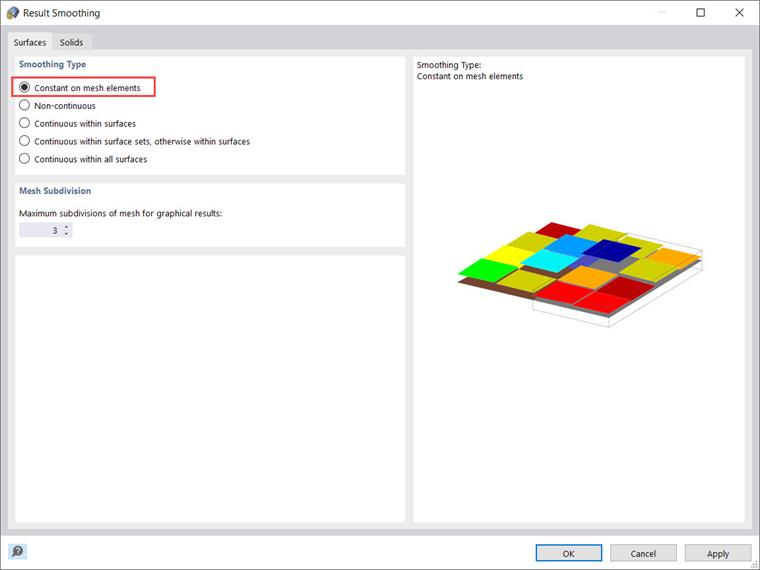
When working with nonlinear material models, the program always performs an iterative calculation. Depending on the model chosen, it defines a different relationship between the stresses and strains. The stiffness of the finite elements is continually adjusted over the course of iterations until the stress-strain relationship is satisfied.
The adjustment is always made for an entire surface or solid element. Therefore, it is recommended to always use the "Constant on mesh elements" smoothing type when evaluating stresses, as shown in Image 11.