This article presents design checks of a rigid column applied to the tension area of the connection. The model is based on an example in the reference literature [1].
System
The column comprises of the cross-section HEB 280 and structural steel S 235 JR.
In Window 1.4 of RF‑/JOINTS, the dimensions of the foundation are specified as 140 x 120 x 80 cm. The concrete class is C20/25.
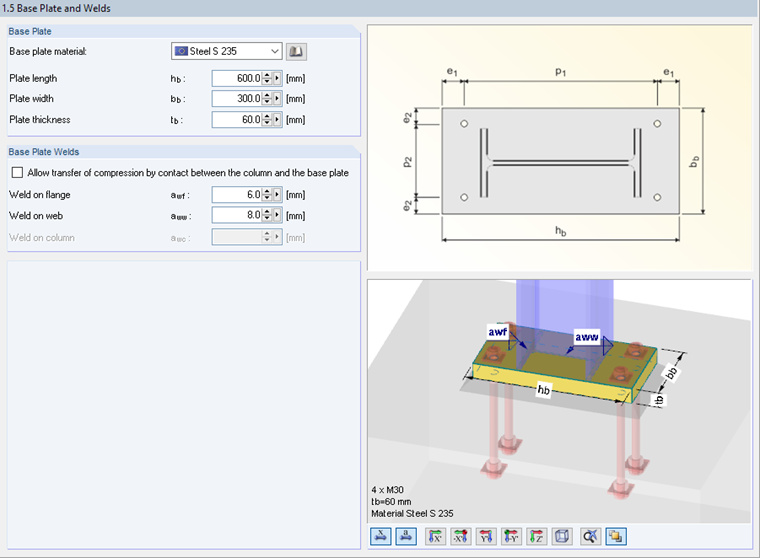
The parameters of the base plate are defined in Window 1.5 as illustrated in Image 02.
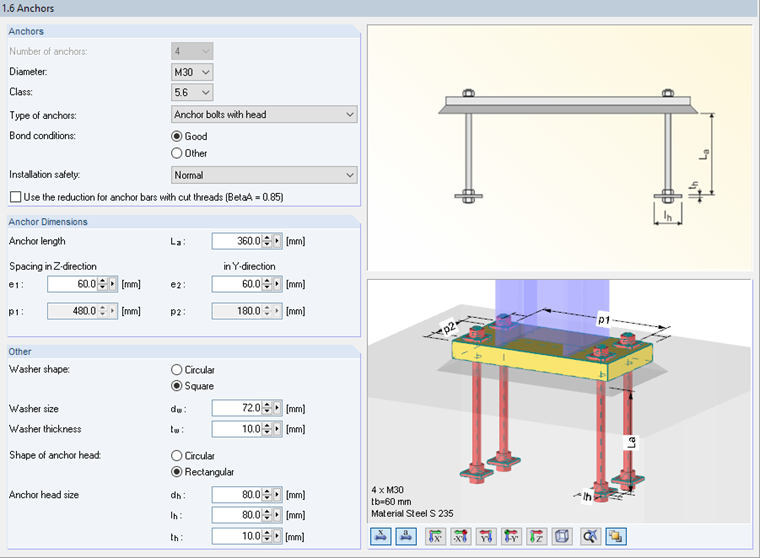
The dimensions and positions of the anchors are defined in Window 1.6 (see Image 03).
Internal forces
RF-/JOINTS allows you to define internal forces manually, and thus independently of the RFEM/RSTAB model.
The following design internal forces are specified in Window 1.3:
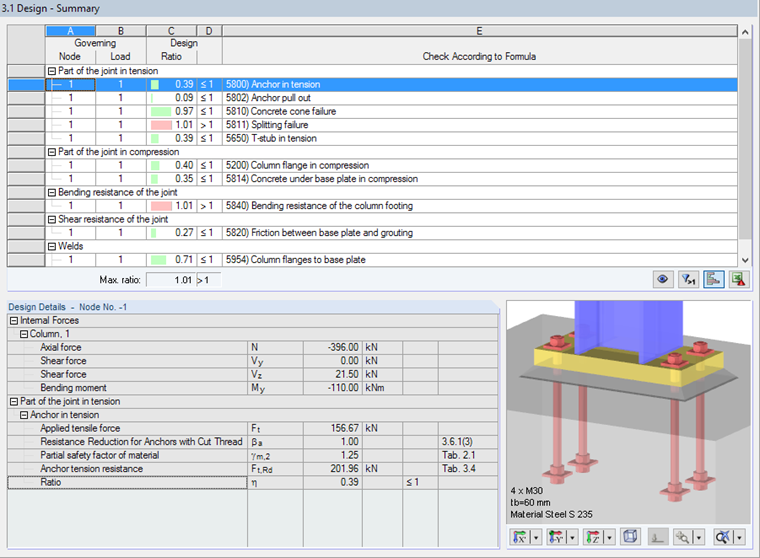
NEd = -396.0 kN
VEd = 21.5 kN
MEd = -110.0 kN
Anchor Forces
In order to determine the design-relevant internal forces, the following case distinctions are necessary:
The "Case F1 < 0 and F2 ≥ 0" is to be assumed as governing for the analysis of the connection in the tension area.
The following section of the article presents design checks of the connection in the tension area with regard to the anchor and the concrete.
Tensile Stress of Anchor
With the anchor M30 (strength 5.6, AS = 5.61 cm²), the design according to [2], Table 3.4, is as follows:
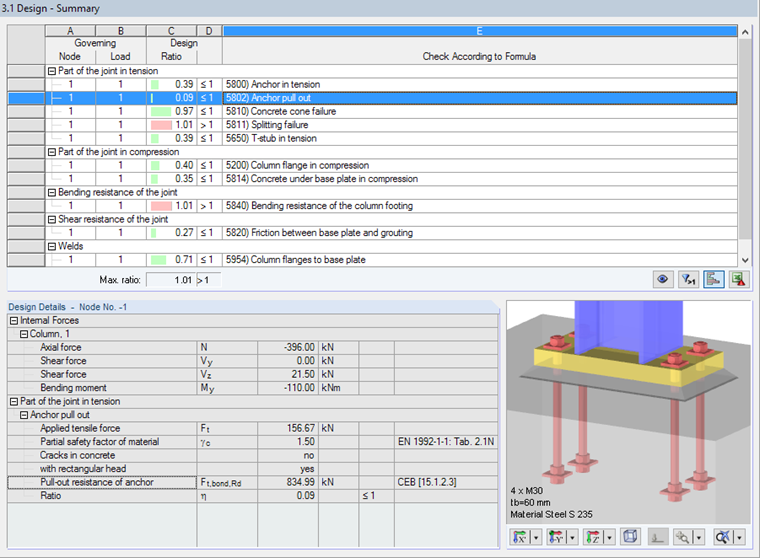
Anchor Pull Out
The resistance to pulling out the anchor is determined according to [4], Section 15.1.2.3, as follows:
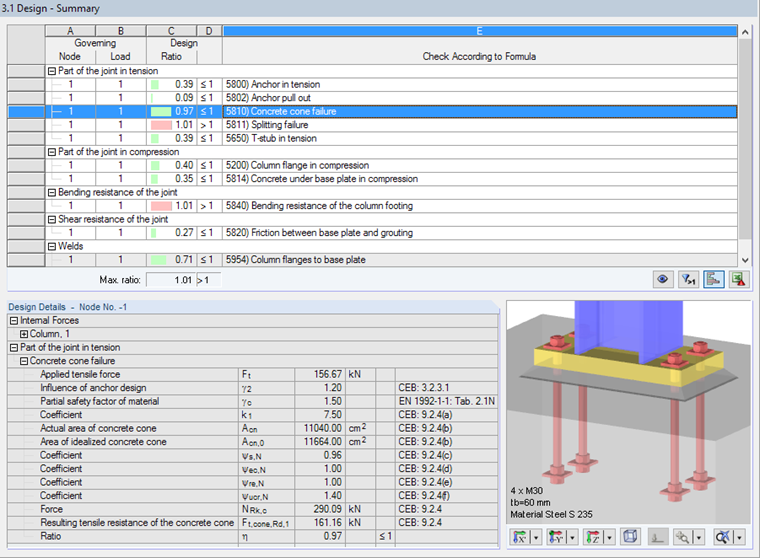
Concrete Cone Failure
In case of the concrete cone failure, a conical break arises from the end of the anchorage element. The concrete cone failure design is performed according to [4], Section 9.2.4.
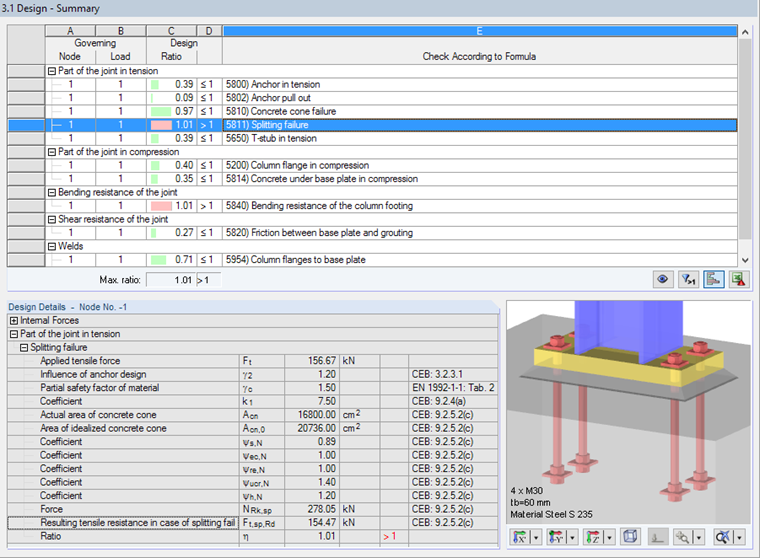
Splitting Failure
Splitting forces cause splitting cracks in the concrete. They occur as radially circumferential around the anchor and thus perpendicular to the tensile force. The splitting failure is also analyzed according to [4], Section 9.2.4.
The tension force resistance of the concrete is exceeded slightly. In this case, the splitting failure governs for the design in the tension areas of the connection.
The analysis for the tension area is completed in the program by designing the tension force introduction. However, this is not further described in this article. Furthermore, it is necessary to design the connection parts in the compression area, the bending resistance of the connection, the shear resistance, and the welds.
Summary
RF-/JOINTS Steel – Column Base designs footings of hinged and restrained column bases. In the case of a column with a base plate subjected to tensile stress, it is necessary to consider the tensile stresses, which arise in the concrete due to the load introduction on the fastener. The tension resistance of the concrete is often governing for the loads that can be transferred by the joint.
![System and Loading According to [1]](/en/webimage/009455/2418877/01-en-png.png?mw=760&hash=7ec548270c812e4679005b311ca774da4860d51a)
![Case Distinction According to [1]](/en/webimage/009458/2418907/04-en-png.png?mw=760&hash=43d2f9b52323d85683e204e06a24e8f962c3a300)