Cables are usually assumed to be flexible in an idealized way. This is due to the fact that they have very low flexural stiffness compared to their strain stiffness. However, in certain cases, the influence of the cable's bending stiffness may be relevant to the calculation of internal forces. Now you can find out what are these cases and what the bending stiffness of a steel cable depends on.
Influence of Cable Cross‑Section on Bending Stiffness
Structural cables are available in a variety of designs and dimensions. Starting with cross-sections with a diameter of a few millimeters, suspension cables of suspension bridges, for example, can reach a diameter of up to one meter. The larger the cable diameter, the greater is the moment of inertia of the cross-section and thus the bending stiffness. Furthermore, the moment of inertia of steel cables depends on the diameter of the individual wires. With the same cross-sectional area, a steel cable consisting of many small individual wires has a lower moment of inertia than a steel cable consisting of a few large individual wires.
Influence of Cable Curvature on Bending Stress
In order to activate the bending stiffness at all, a cable curvature is required. The bending stresses resulting from the curvature can be roughly estimated using the Reuleaux's normal bending stress equation.
Bending stress becomes governing especially in highly curved cable sections, such as those that may occur at the load application points of concentrated loads or when the cable runs over a pulley.
Comparison of Flexible and Rigid Cable
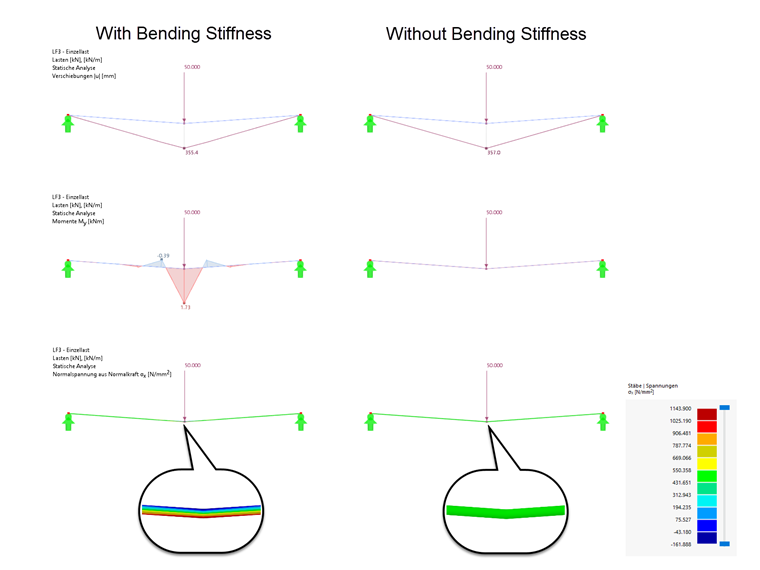
The following example shows a horizontally tensioned cable that is loaded in the center by a vertical concentrated load. For this structural system, the results are compared once for a rigid cable and once for an ideal flexible cable.
While the influence of the cable's bending stiffness on the total deformation is negligible, there are clear differences in the internal forces. In contrast to the ideal cable, the bending-resistant cable can absorb bending moments and shear forces in addition to axial forces. The normal stresses in the entire structural system are similar for both variants. It is only in the area of the load application point where the cable is subjected to severe bending, that is, significant stress peaks occur in the rigid cable.
Avoidance of Large Bending Normal Stresses
To avoid oversizing of the cable, the cable bending stresses should be minimized as much as possible. On the one hand, this can be achieved by avoiding strong cable curvatures, for example, by increasing the diameter of deflection pulleys. On the other hand, it is also possible to reduce the diameter of the individual wires in order to reduce the cable bending stress. A steel cable consisting of many small individual wires is less susceptible to bending stress than a cable consisting of a few large individual wires.