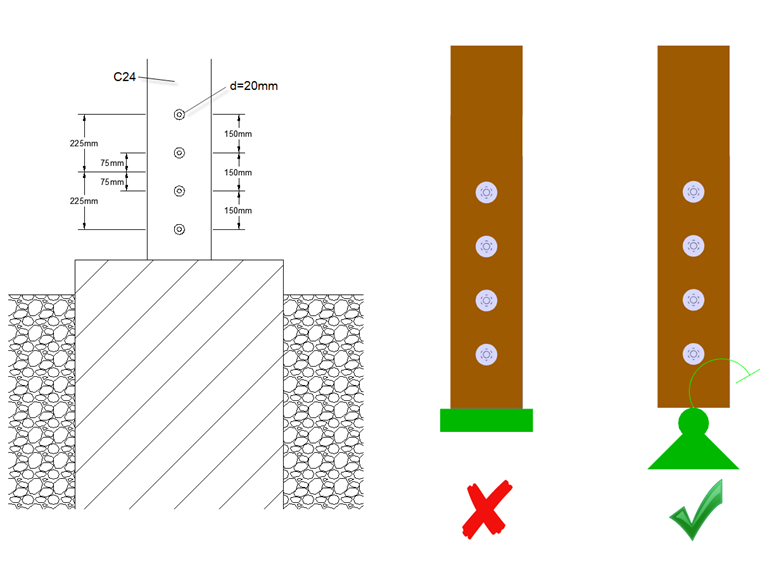
Moment d'inertie polaire
Le moment d'inertie polaire de l'assemblage représenté sur la Figure 01 est calculé comme suit :
|
Ip |
Polares Trägheitsmoment ohne Anteil der Verbindungsmittelflächen |
|
xi |
Abstand vom Schwerpunkt der Verbindungsmittelgruppe zum Verbindungsmittel in x-Richtung |
|
yi |
Abstand vom Schwerpunkt der Verbindungsmittelgruppe zum Verbindungsmittel in y-Richtung |
Ip = 752 + 752 + 2252 +2252 = 112,500 mm2
Détermination du module de glissement à l'ELS
Le module de glissement à l'état limite de service peut être calculé selon le Tableau 7.1 de [1]. Pour des broches de 20 mm de diamètre en bois résineux C24, on obtient le résultat suivant par plan de cisaillement :
|
Kser |
Verschiebungsmodul pro Scherfuge |
|
ρm |
Mittelwert der Rohdichte in kg/m³ |
|
d |
Durchmesser des Verbindungsmittel |
Kser = 4201,5 ⋅ 20/23 = 7 485 N/mm = 7 485 kN/m
Ainsi, il existe deux plans de cisaillement pour une plaque métallique internes. De plus, le module de glissement doit être multiplié par 2,0 pour les assemblages bois-métal selon le Chapitre 7.1 (3) de [1]. Le module de glissement de la broche peut ainsi être déterminé comme suit :
Kser= 2 ⋅ 2 ⋅ 7,485 kN/m = 29,940 kN/m
Détermination du module de glissement à l'ELU
Selon [1], le module de glissement pour l'état limite ultime d'un assemblage Ku doit être supposé comme suit :
|
Ku |
Anfangsverschiebungsmodul |
|
Kser |
Verschiebungsmodul eines Verbindungsmittels |
Ku = 2/3 ⋅ 29,940 kN/m = 19,960 kN/m
Dans [2] et [3], il est nécessaire de considérer la valeur de calcul du module de glissement d'un assemblage.
|
Kd |
Bemessungswert des Verschiebungsmoduls |
|
Ku |
Anfangsverschiebungsmodul |
|
γM |
Teilsicherheitsbeiwert für Verbindungen gemäß [1] Tabelle 2.3 |
Kd = 19,960 kN/m / 1,3 = 15,354 kN/m
Détermination de la rigidité du ressort
La valeur de calcul du module de glissement devant être calculée pour la vérification à l'ELU et la valeur moyenne pouvant être supposée à l'ELS, on obtient deux rigidités de ressort.
|
Cφ,SLS |
Drehfedersteifigkeit für den Grenzzustand der Gebrauchstauglichkeit |
|
Kser |
Verschiebungsmodul eines Verbindungsmittels |
|
Ip |
Polares Trägheitsmoment ohne Anteil der Verbindungsmittelflächen |
Cφ,SLS = 29,940 N/mm ⋅ 112,500 mm2 = 3,368 kNm/rad
|
Cφ,ULS |
Drehfedersteifigkeit für den Grenzzustand der Tragfähigkeit |
|
Kd |
Bemessungswert des Verschiebungsmoduls |
|
Ip |
Polares Trägheitsmoment ohne Anteil der Verbindungsmittelflächen |
Cφ,ULS= 15 354 N/mm ⋅ 112 500 mm2= 1 727 kNm/rad
Pour considérer ces deux valeurs dans un calcul, on peut activer l'onglet « Modifier la rigidité » dans les paramètres de calcul des combinaisons de charges. Ainsi, comme dans cet exemple, la rigidité du ressort de rotation pour toutes les combinaisons d'ELU peut être multipliée par le facteur Cφ, ELU/Cφ,ELS. La valeur de Cφ, à l'ELS est entrée dans les conditions d'appui ou d'articulation. Vous pouvez effectuer le calcul avec une rigidité de ressort en torsion de 1,727 kNm/rad dans toutes les combinaisons ELU et avec 3,368 kNm/rad dans toutes les combinaisons ELS. Cette opération est expliquée dans la vidéo ci-contre.
Dans cet exemple, la rotation élastique des fondations est considérée comme infinie et n'est pas prise en compte.
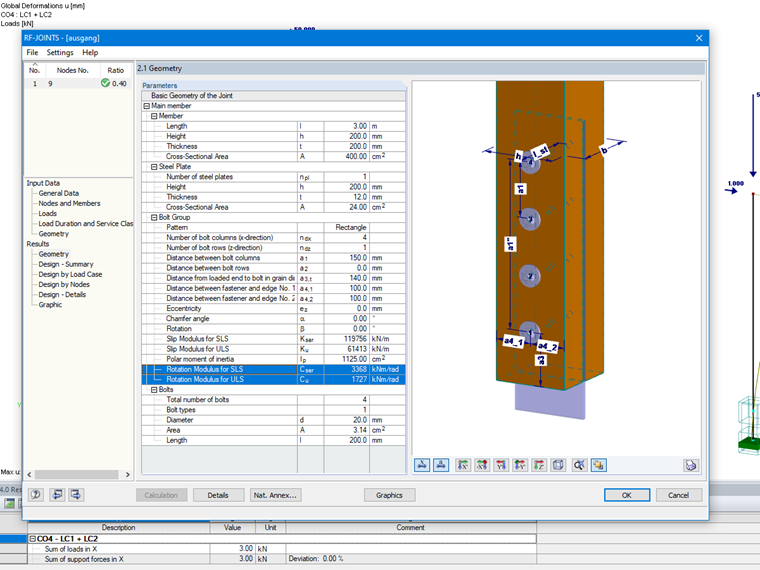
Détermination de la rigidité de ressort de torsion à l'aide du module additionnel RF-/JOINTS Timber - Steel to Timber
Lors du calcul de l'assemblage avec RF-/JOINTS Timber - Steel to Timber, les résultats des rigidités de torsion des ressorts sont également affichés (voir la Figure 02). Dans RSTAB, il est nécessaire de les adapter manuellement aux conditions d'appui ou d'articulation. Dans RFEM, cette opération peut être effectuée automatiquement. Les assemblages sont créés automatiquement dans RFEM et la rigidité est considérée en conséquence. Cette opération est expliquée dans la vidéo ci-contre.