Back to Knowledge Base
Is this page helpful?
12982x
000787
Dipl.-Ing. (FH) Gerhard Rehm
2021-03-29

Considering Elastic Slip Modulus of Timber Connection

For a timber connection as shown in Figure 01, you can take into account the torsional spring rigidity (spring stiffness for rotation) of the connections. You can determine it by means of the slip modulus of the fastener and the polar moment of inertia of the connection.

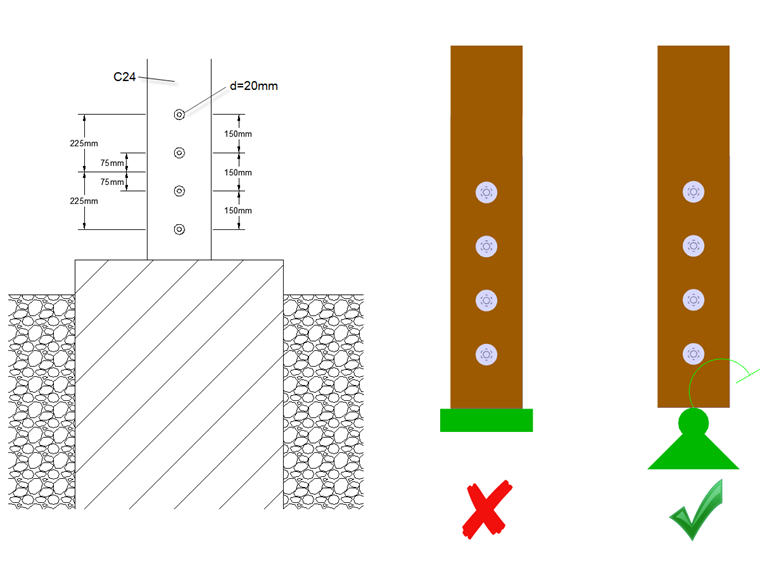
Flexibility of Timber Connection
Flexibility of Timber Connection

Polar Moment of Inertia

The connection's polar moment of inertia shown in Figure 01 results in:

Ip = ∑xi2i=1n + ∑yi2i=1n

Ip

Polares Trägheitsmoment ohne Anteil der Verbindungsmittelflächen

xi

Abstand vom Schwerpunkt der Verbindungsmittelgruppe zum Verbindungsmittel in x-Richtung

yi

Abstand vom Schwerpunkt der Verbindungsmittelgruppe zum Verbindungsmittel in y-Richtung
Polar Moment of Inertia

Ip = 752 + 752 + 2252 +2252 = 112,500 mm2

Modulus of Displacement Determination for the Serviceability Limit State

The modulus of displacement for the serviceability limit state can be calculated according to [1], Table 7.1. For bolts with a diameter of 20 mm in C24 softwood, the modulus per shear plane is calculated as follows:

Kser = ρm1.5 · d23

Kser

Verschiebungsmodul pro Scherfuge

ρm

Mittelwert der Rohdichte in kg/m³

d

Durchmesser des Verbindungsmittel
Modulus of Displacement per Shear Plane

Kser = 4201.5 ⋅ 20/23 = 7,485 N/mm = 7,485 kN/m

This results in two shear planes for an internal steel plate. In addition, the modulus of displacement should be multiplied by a factor of 2.0 for steel plate-timber connections according to [1], Chapter 7.1 (3). You can determine the modulus of displacement for the bolt as follows:

Kser= 2 ⋅ 2 ⋅ 7,485 kN/m = 29,940 kN/m

Modulus of Displacement Determination for the Ultimate Limit State

According to [1], the modulus of displacement of a connection in the ultimate limit state, Ku, has to be assumed as follows:

Ku = 23 · Kser

Ku

Anfangsverschiebungsmodul 

Kser

Verschiebungsmodul eines Verbindungsmittels
Initial Modulus of Displacement

Ku = 2/3 ⋅ 29,940 kN/m = 19,960 kN/m

[2] and [3] require considering the design value of the modulus of displacement of a connection.

Kd = KuγM

Kd

Bemessungswert des Verschiebungsmoduls

Ku

Anfangsverschiebungsmodul 

γM

Teilsicherheitsbeiwert für Verbindungen gemäß [1] Tabelle 2.3
Design Value of Modulus of Displacement

Kd = 19,960 kN/m / 1.3 = 15,354 kN/m

Torsional Spring Stiffness Determination

For the ultimate limit state design, you have to use the design value of the slip modulus for calculation and the mean value for the serviceability limit state design; thereby you obtain two torsional spring rigidities.

Cφ,SLS = Kser · Ip

Cφ,SLS

Drehfedersteifigkeit für den Grenzzustand der Gebrauchstauglichkeit

Kser

Verschiebungsmodul eines Verbindungsmittels

Ip

Polares Trägheitsmoment ohne Anteil der Verbindungsmittelflächen
Torsional Spring Stiffness for Serviceability Limit State

Cφ,SLS = 29,940 N/mm ⋅ 112,500 mm2 = 3,368 kNm/rad

Cφ,ULS = Kd · Ip

Cφ,ULS

Drehfedersteifigkeit für den Grenzzustand der Tragfähigkeit

Kd

Bemessungswert des Verschiebungsmoduls

Ip

Polares Trägheitsmoment ohne Anteil der Verbindungsmittelflächen
Rotational Spring Stiffness for Ultimate Limit State

Cφ,ULS= 15,354 N/mm ⋅ 112,500 mm2= 1,727 kNm/rad

To take both rigidities into account, activate the "Modify Stiffness" sub-tab (select the corresponding check box in the Calculation Parameters sub-tab of the Load Combinations tab in the Edit Load Combinations and Calculations dialog box). As in this example, this allows you to multiply the torsional spring rigidity for all SLS combinations by Cφ,ULS / Cφ,SLS. The value of Cφ,SLS is entered in the support or hinge conditions. Thus, you can calculate with a torsional spring rigidity of 1.727 kNm/rad in all ULS combinations and with 3.368 kNm/rad in all SLS combinations. This approach is also shown in the video.

In this example, the elastic foundation rotation is considered to be infinite and is not taken into account.

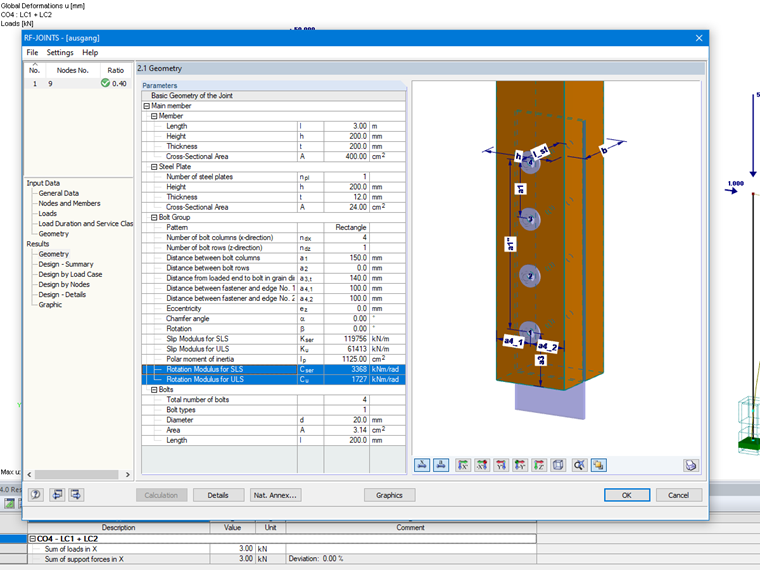
Torsional Spring Stiffness Determination Utilizing RF-/JOINTS Timber - Steel to the Timber Add-on Module

When calculating the connection with RF-/JOINTS Timber - Steel to Timber, the results of the torsional spring stiffnesses are also displayed (see Figure 02). In RSTAB, you have to transfer them manually to the support or hinge conditions. In RFEM, this can be done automatically. The connections are automatically created in RFEM and the stiffness is adopted accordingly. The video shows the procedure.

Rotational Spring Stiffness in RF-/JOINTS Timber - Steel to Timber
Rotational Spring Stiffness in RF-/JOINTS Timber - Steel to Timber

EN-US | Flag Knowledge Base
KB 000787 | Considering Elastic Slip Modulus of Timber Connection
Author

Mr. Rehm is responsible for developing products for timber structures, and he provides technical support for customers.

Links
References
  1. Austrian Standards. (2015). Eurocode 5: Design of Timber Structures – Part 1-1: General – Common Rules and Rules for Buildings; DIN EN 1995-1-1:2010-12. Berlin: Beuth Verlag GmbH.
  2. DIN. (2013). National Annex – Eurocode 5: Design of Timber Structures – Part 1-1: General – Common Rules and Rules for Buildings, DIN EN 1995-1-1/NA:2013-08. Berlin: Beuth Verlag GmbH.
  3. Austrian Standards. (2015). Eurocode 5: Design of Timber Structures – Part 1-1: General – Common Rules and Rules for Buildings. Consolidated Version with national specifications, national comments and national supplements for the implementation of OENORM EN 1995-1-1; ÖNORM B 1995-1-1:2015-06-15.
  • Mia: AI Assistant
  • Latest FAQ
Events
Videos
Models to Download
Knowledge Base Articles
Illustration of a method for performing stability analysis according to DIN EN 1992-1-1 in RFEM 6
For reinforced concrete components and structures whose structural behavior is significantly influenced by the second-order effects, Eurocode 2 provides the general method based on a nonlinear determination of internal forces according to the second-order analysis (5.8.6), as well as an approximation method based on the nominal curvature (5.8.8).

The aim of this technical article is to perform a design according to the general design method of Eurocode 2, using the example of a slender reinforced concrete column.
Modell eines Stahlbetonbalkens, der durch Kriechen und Schwinden beeinflusst wird
This technical article addresses the direct deformation analysis of reinforced concrete beams considering the long-term effects of creep and shrinkage. The direct calculation according to Eurocode 2 (EN 1992-1-1, Section 7.4.3) is explained using a single-span beam. Particular emphasis is placed on tension stiffening, behavior in the cracked state based on the distribution factor (damage parameter), and consideration of shrinkage and creep behavior.
Illustration of equivalent lateral force method for seismic analysis in structural engineering
This article provides a comprehensive overview of essential seismic analysis methods, explaining their principles and applications, as well as the scenarios in which they are most effective
Design of structural walls using Dlubal software solutions.
This article provides a step-by-step guide to the design of shear walls in RFEM 6.
Screenshots
Product Features
Material model Anisotropic | Damage, nonlinear behavior, concrete and reinforced concrete

The "Nonlinear Material Behavior" add-on includes the Anistropic | Damage material model for concrete structural components. This material model allows you to consider concrete damage for members, surfaces, and solids.

You can define an individual stress-strain diagram via a table, use the parametric input to generate the stress-strain diagram, or use the predefined parameters from the standards. Furthermore, it is possible to consider the tension stiffening effect.

For the reinforcement, both nonlinear material models "Isotropic | Plastic (Members)" and "Isotropic | Nonlinear Elastic (Members)" are available.

It is possible to consider the long-term effects due to creep and shrinkage using the "Static Analysis | Creep & Shrinkage (Linear)" analysis type that has been recently released. Creep is taken into account by stretching the stress-strain diagram of the concrete using the factor (1+phi), and shrinkage is taken into account as the pre-strain of the concrete. More detailed time step analyses are possible using the "Time-Dependent Analysis (TDA)" add-on.

Feature 002918 | Determination of Required Longitudinal Reinforcement for Direct Crack Analysis

In the Concrete Design add-on, you can determine the required longitudinal reinforcement for the direct crack width analysis (w k).

Feature 002920 | Automatic Function of Longitudinal Reinforcement for Members

For the design of reinforced concrete members, there is the option to automatically determine the number or diameter of rebars.

Feature 002876 | Reinforcement Results in Tables by Design Situation

For concrete design, you can display the reinforcement results in tables separately by design situation.

Frequently Asked Questions (FAQ)
In the case of the serviceability limit state design (for example, of a steel beam), the precamber is not taken into account. Is this a program error or is my entry incorrect?

Why is the effective depth different with the effective depth used in shear checks?

How can I check the determination of the required reinforcement?
I have created a model in which the ceiling slab is lined with ribs. When I assign a Rib member type to the boundary line of the surface and align it to the bottom edge of the surface, the boundary line is automatically pulled towards the center of gravity of the rib, that is, downwards under the slab. Is there a way to change this so that my lines still appear at the edge of the surface?
Is it possible to view the tangential and radial analysis results and reinforcement requirements rather than orthogonal for a circular slab?
How can I perform member design by case for different settings in the design configuration?
Customer Projects
Recommended Products for You