20930x

001491

Dipl.-Ing. (BA) Markus Baumgärtel

7.11.2017

Stanovení součinitele síly a výsledných zatížení na pruty od zatížení větrem u rovinné příhradové konstrukce

Na jednoduchém příkladu příhradového vazníku si ukážeme, jak lze počítat zatížení větrem v závislosti na plnosti příhradoviny.

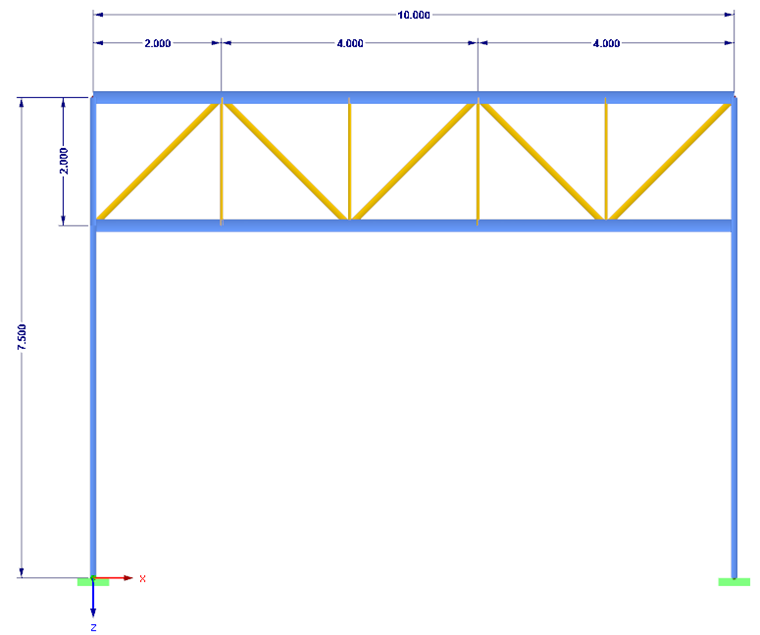
Vítr kolmo na konstrukci

Abmessungen des Rahmens

Základní rychlost větru v_b = 25,0 m/s
Základní dynamický tlak větru q_b = 0,39 kN/m²
Maximální dynamický tlak

q_{p} (z) = 1, 7 \cdot q_{b} \cdot {(\frac{z}{10})}^{0, 37} = 1, 7 \cdot 0, 39 \cdot {(\frac{7, 5}{10})}^{0, 37} = 0, 596 kN / m ²

Vzorec 1

Součinitel síly cf pro příhradové konstrukce:

c_{f} = c_{f, 0} \cdot Ψ_{λ}

Vzorec 2

Stanovení součinitele síly c_f,0pro příhradové konstrukce bez uvažování koncových vírů pomocí součinitele plnosti φ

Součinitel plnosti:

φ = \frac{A}{A_{C}}

Vzorec 3

kde
A = součet průmětů ploch prvků
A_C = l ⋅ b = celková plocha obálky

Poměr ploch příhradové konstrukce:

A = 2, 828 m \cdot 0, 1 m \cdot 5 + 2, 0 m \cdot 0, 05 m \cdot 4 + 2, 0 m \cdot 0, 1 m \cdot 2 +

10 m \cdot 0, 2 m \cdot 2 = 6, 214 m ²

A_{C} = 10 m \cdot 2 m = 20 m ²

Vzorec 4

Anzeige der Parameter zur Bestimmung der Völligkeit in RFEM/RSTAB

Součinitel plnosti:

φ = \frac{6, 214 m ²}{20 m ²} = 0, 3107

Vzorec 5

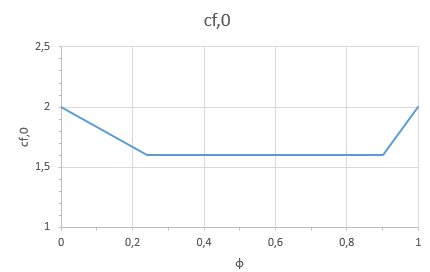
Jakmile známe hodnotu součinitele plnosti, můžeme odečíst hodnotu součinitele síly c_f,0 například z obrázku 7.33 v normě ČSN EN 1991-1-4 [1]. Součinitel síly tak je 1,6.

Součinitel síly cf,0

Dále je třeba pro stanovení součinitele koncového efektu Ψ_λ vypočítat efektivní štíhlost konstrukčního prvku.

Efektivní štíhlost λ (tab. 7.16 → ČSN EN 1991-1-4 [2])

λ = 2 \cdot \frac{10 m}{2 m} = 10 < 70 \to 10 je rozhodující

Vzorec 6

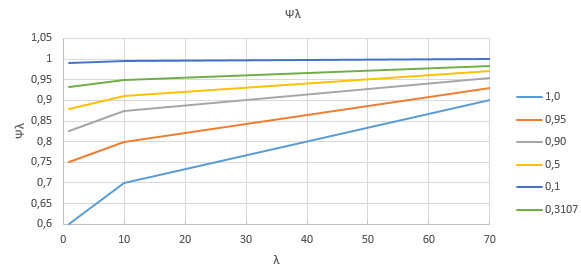
Na základě spočítaných hodnot můžeme z diagramu na obrázku 7.36 v normě určit hodnotu součinitele koncového efektu Ψ_λ na 0,95.

Součinitel koncového efektu Ψλ

Součinitel síly se tak stanoví následovně:

c_{f} = c_{f, 0} \cdot Ψ_{λ} = 1, 6 \cdot 0, 95 = 1, 52

Vzorec 7

Výpočet výsledného zatížení příhradové konstrukce větrem

Varianta 1: Ekvivalentní statické zatížení F_w

F_{w} = c_{f} \cdot q_{p} (z) \cdot A_{ref}

Vzorec 8

kde
A_ref = průmět plochy

F_{w} = 1, 52 \cdot 0, 596 kN / m ² \cdot 6, 214 m ² = 5, 63 kN

Vzorec 9

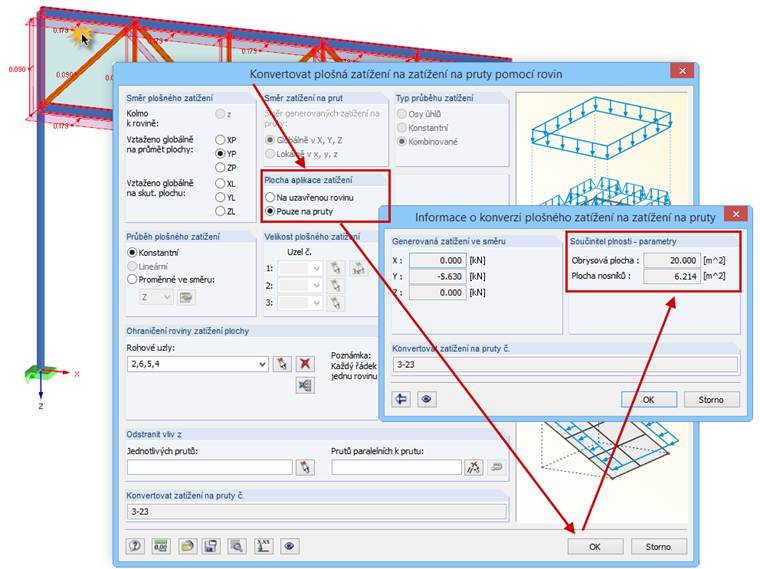
Varianta 2: Zatížení jako zatížení na pruty z plošného zatížení

F_{w 1} = 1, 52 \cdot 0, 596 kN / m ² = 0, 91 kN / m ²

Vzorec 10

Má-li se toto plošné zatížení v programu RFEM/RSTAB rozdělit skutečně pouze na pruty, je nezbytné vybrat pro oblast aplikace zatížení možnost „Pouze na pruty“. Po zadání zatížení a kliknutí na tlačítko [OK] se součet uvažovaného zatížení znovu zobrazí v informačním okně.

Autor

Ing. Baumgärtel zajišťuje technickou podporu zákazníkům společnosti Dlubal Software.

Odkazy

Reference

Eurokód 1: Zatížení konstrukcí - Část 1-4: Obecné účinky, Zatížení větrem; BS EN 1991-1-4:2010-12
Národní příloha - Národně stanovené parametry - Eurokód 1: Zatížení konstrukcí - Část 1-4: Obecná zatížení – Zatížení větrem; ČSN EN 1991-1-4:2007-04

Stahování

Model v programu RSTAB

244 KB

;