Optionally, EN 1993-1-1, Section 5.2.1 (4), Expression 5.2 provides a simplified calculation for movable frame structures in buildings (portal frames with shallow roof slope < 26° and beam-and-column type plane frames in buildings):
where
HEd = the total design horizontal load (including potential story shear)
VEd = the total design vertical load (including potential story thrust)
δH,Ed = the horizontal displacement at the top of the story, relative to the bottom of the story subjected to HEd
h = story height
This approach applies if the effect of the axial compression in the rafters on the critical load is small. This can be checked using Expression 5.3 mentioned in Note 2B:
This equation corresponds exactly to the element (739) of DIN 18800-1, but with a reversed condition.
The basis of this method is the P-delta analysis. However, Expression 5.2 can also be derived from the Dischinger factor by the relation of the initial moment M0 to the additional moment ∆M:
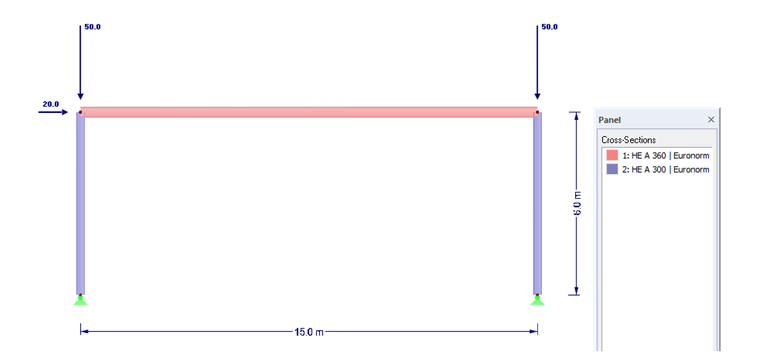
Example
The calculation is illustrated on the following example of a movable frame.
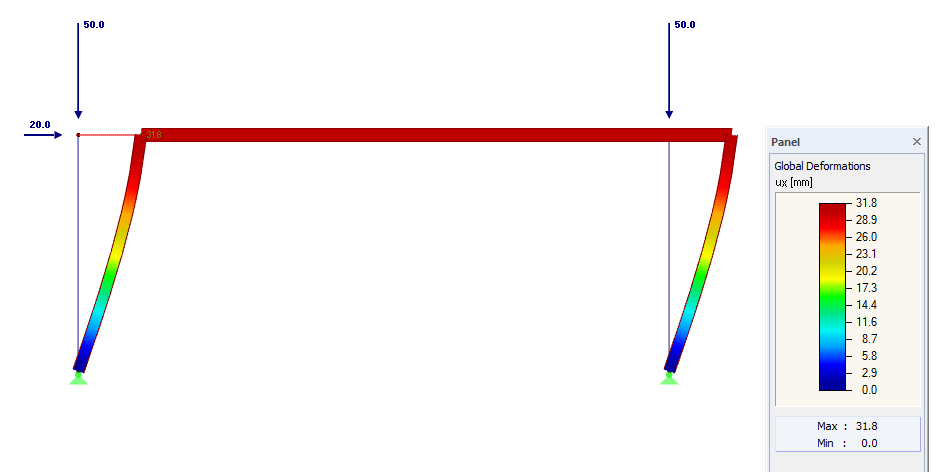
These initial values are used in Equation 5.2, resulting in a critical load factor of:
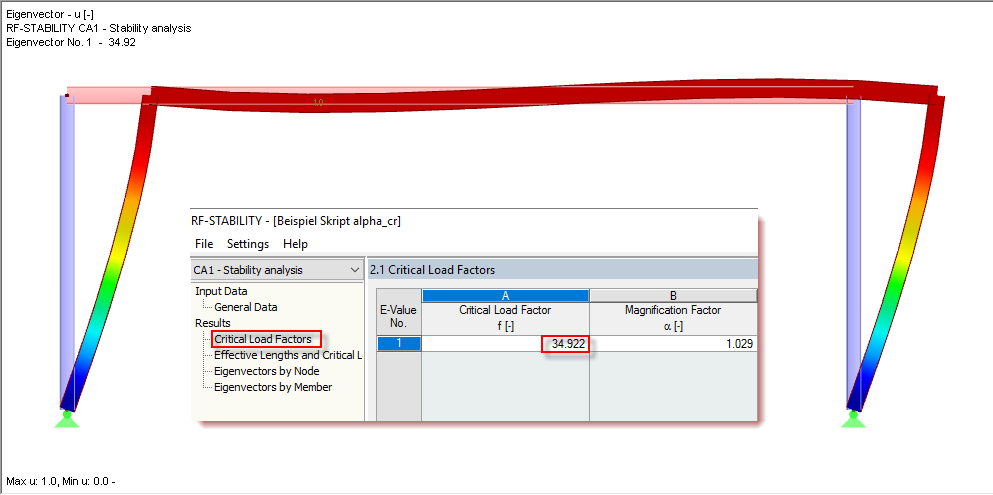
RF-STABILITY (linear eigenvalue solver) or RSBUCK allows you to quickly determine the exact result of the critical load factor as well as the mode shape with antimetric stability failure.
.png?mw=760&hash=acc6a96b53f58aee73eefe3d9e14a16d856b5b6d)
.png?mw=760&hash=612208b5e1fef1338f89efe8f7394f1d23b20063)