Influence of Various Integration Methods on Calculation of Steel Fiber-Reinforced Concrete Slab
Technical Article
Using an example of a steel fiber-reinforced concrete slab, this article describes how the use of different integration methods and of a different number of integration points affects the calculation result.
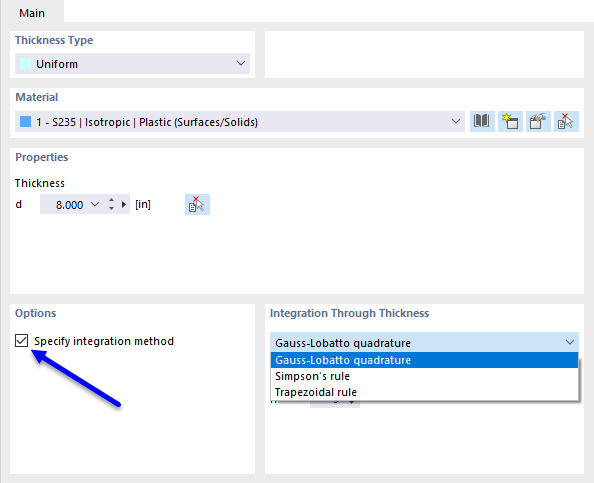
As explained in the technical article about the User-Defined Integration Method for Determining Internal Forces in Slabs in RFEM 6, the internal forces and moments available in slabs result from the numerical integration of stresses occurring over the slab thickness. If a nonlinear material is used, you can choose between the Gauss-Lobatto quadrature, the trapezoidal rule, and the Simpson's rule in RFEM 6. It is also possible to specify the number of integration points from 3 to 99.
The theory about the integration methods is described in the Multilayer Surfaces manual. In this manual, you also find a similar example for a point-supported three-layer slab.
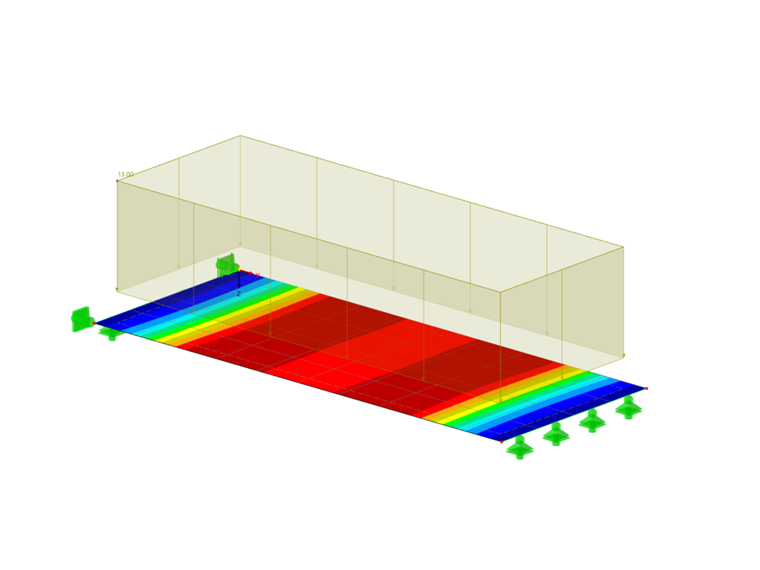
In this example describing a steel fiber-reinforced concrete slab, we want to show the effect concerning the difference of using several integration methods and of a different number of integration points on the calculation result. For this purpose, we consider a slab that is 5 m long (about 16 ft), 2 m wide (about 6 ft) and 30 cm thick (almost 1 ft), for which the Isotropic Damage material model is used. A load of 13 kN/m² is applied and the mesh density is 0.5 m (1.6 ft).
The integration method as well as the number of integration points can be specified in the main data of the plate thickness.
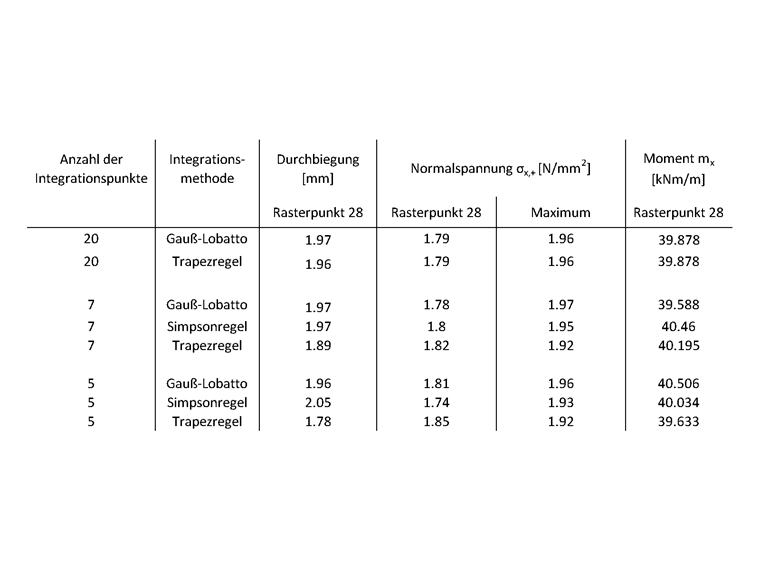
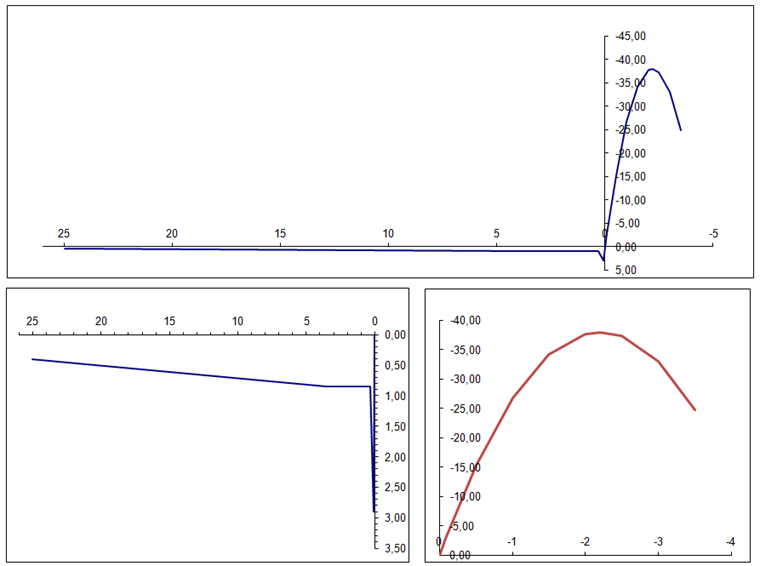
The calculation provides the following results, and the plate's center (grid point no. 28) is considered in particular.
For a small number of integration points, there are visible deviations among the individual integration methods. The trapezoidal rule in particular is less accurate. For a larger number, however, the results of all integration methods approach a fixed solution. The Gauss-Lobatto quadrature with 9 integration points used by default in RFEM 6 is sufficient for most cases. However, if you apply a very high load on the slab, the differences between the integration methods become even more apparent.
In particular, if your calculation reaches into the steel fiber-reinforced concrete's yielding range, a higher number of integration points is useful, as the material behavior can be better represented in this way. The stress-strain behavior in this range can be only imprecisely approximated by polynomials, which is, however, what the numerical integration methods are based on. Therefore, it may be worth to use the trapezoidal or the Simpson's rule in this case, since these rules are each applied to a smaller area and the partial results are added then.
The material behavior of steel fiber-reinforced concrete is explained in this link article.
Keywords
Steel Fiber-Reinforced Concrete Integration Method Integration Points
Links
Write Comment...
Write Comment...
Contact Us
Do you have further questions or need advice? Contact us via phone, email, chat, or forum, or search the FAQ page, available 24/7.
New
Fatigue Design According to EN 1992-1-1 in RFEM
This article describes the fatigue design according to EC2 (EN 1992-1-1) for the Concrete Design add-on.
Associated Products
Main Program
The structural analysis program RFEM 6 is the basis of a modular software system. The main program RFEM 6 is used to define structures, materials, and loads of planar and spatial structural systems consisting of plates, walls, shells, and members. The program can also design combined structures as well as solid and contact elements.
4,450.00 EUR
Concrete Design for RFEM 6
Design
In the Concrete Design add-on, various designs according to international standards are possible. You can design members, surfaces, and columns, as well as perform punching and deformation analyses.
2,650.00 EUR
Nonlinear Material Behavior for RFEM 6
Additional Analysis
The Nonlinear Material Behavior add-on allows you to consider material nonlinearities in RFEM (e.g., isotropic plastic, orthotropic plastic, isotropic damage).
1,450.00 EUR
