Cross-Section
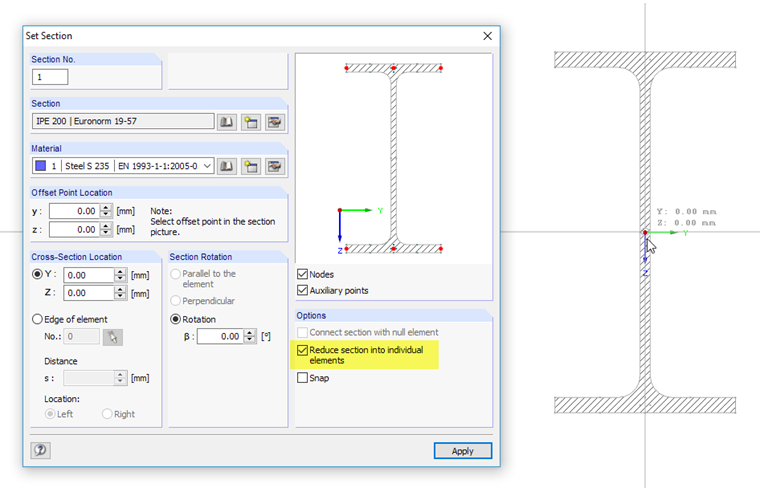
The cross-section is created using the cross-section library. When setting the rolled section IPE 200, the “Reduce section into individual elements” option is activated. The material of the section is structural steel S 235.
The notch can be generated by dividing the web element at a distance of 30 mm. Then, you can remove the overlapping elements and fillets.
Internal Forces
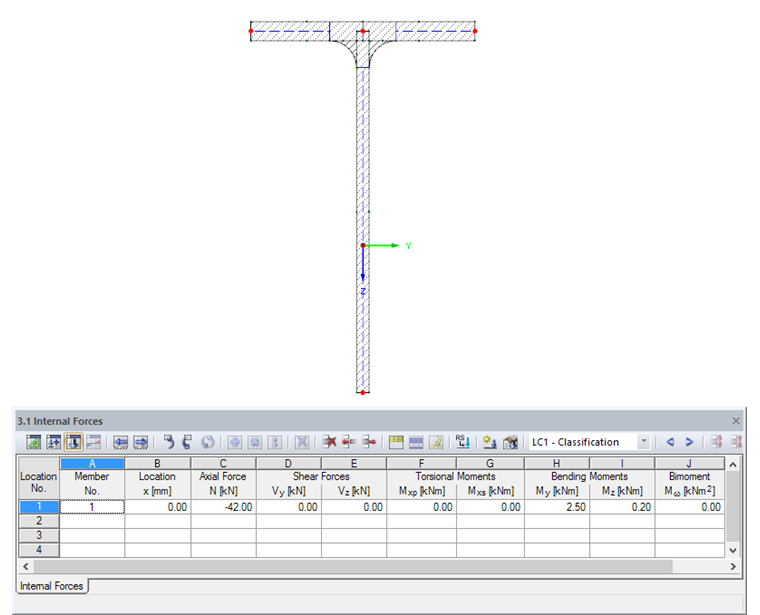
In our example, a very large compression force with small bending moments is specified.
Constellations of internal forces can be analyzed using diverse load cases, x-locations, or member numbers. In addition, SHAPE-THIN provides the option to import the internal forces from RFEM or RSTAB.
Cross-section Classification
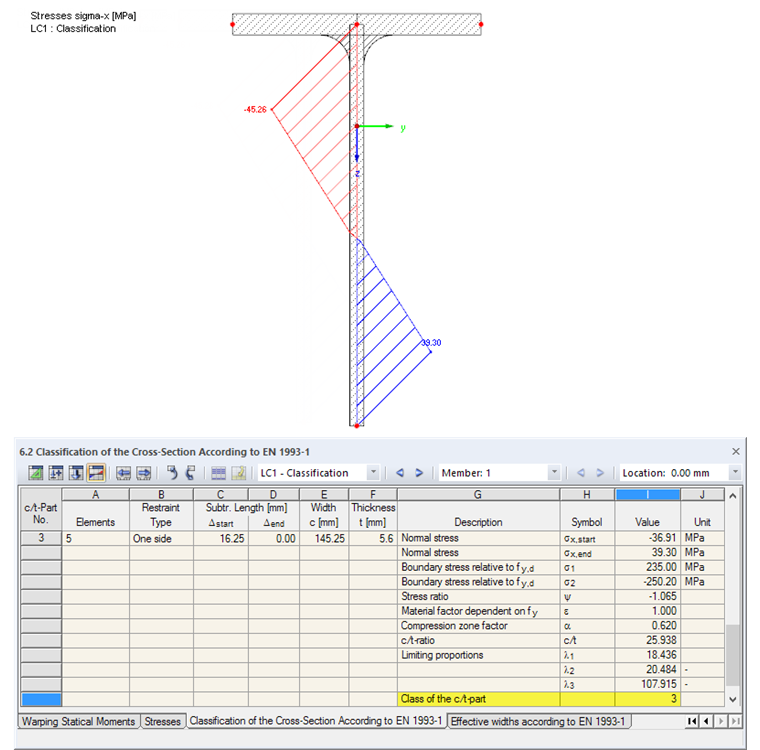
After the calculation, Cross-Section Class 1 is assigned to the flanges. The web belongs to Cross-Section Class 3.
In order the web would reach the yield strength for an elastic stress distribution, the plastic moment resistance cannot develop due to local buckling. Anyway, the local buckling does not occur before reaching the yield strength.
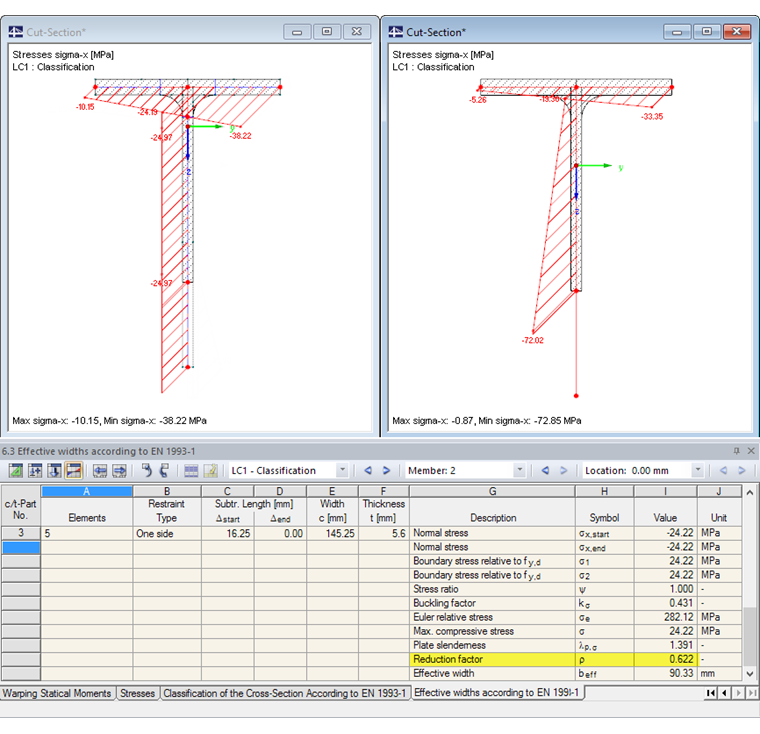
Effective Cross-Sections
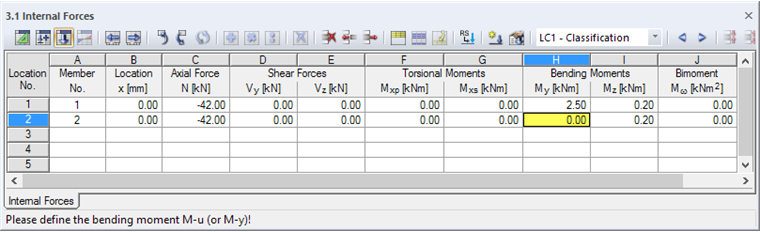
As you can see in the stresses graphic, the bending moment My reduces the compressive stresses at the free edge of the web. For further design, this moment is set to zero. The modified constellation of internal forces can be assigned to a new member, for example, associated with a new crew.
As a result, the web is now assigned to Cross‑Section Class 4. The effective width of the cross-section part is only 62% of the member length.
The stresses can be displayed both on the full cross‑section (on the top left in the figure) and on the reduced cross‑section (right).
Plastic Design
In SHAPE-THIN, it is also possible to perform the plastic analysis for both constellations of internal forces. To do this, it is necessary to select the “Plastic capacity design” option in the General Data dialog box. In this design, the enlargement factor αplast is determined as the maximum of a linear optimization task in order to reach the plastic cross‑section resistance, taking into account the interaction conditions (“Revised Simplex Algorithm”).
The simplex calculation gives the result of plastic reserves of 541% and 862% for both member internal forces.
It is apparent that the failure risk of the cross-section resistance is far higher in the case of compression (Member 2) than in the case of the combined effects, although only a part of the web is effective according to Eurocode 3. However, in this analysis, the different approaches of the two methods must not be mixed: according to Eurocode 3, it is disputable whether a cross‑section part is prone to buckling. This is the case of the Class 4 cross-sections. Then, it is necessary to analyze whether the remaining effective cross‑section is able to absorb the internal forces. On the other hand, the Simplex Method performs a plastic calculation of stresses, which is not affected by the c/t ratios of the cross‑section parts. Therefore, there is no analysis of local buckling, only a plastic stress analysis.
Summary
SHAPE-THIN performs classification of thin-walled cross-sections according to EC 3 and EC 9 by determining effective widths as well as effective cross-section properties. Stresses can be checked accordingly with regard to a reduced cross-section. In contrast, the plastic analysis according to Simplex Method does not consider any local buckling effects. This may lead to more favorable design ratios. However, these are not achieved in the cross-section because of stability failure.
.png?mw=350&hash=83397b9718189d605563213de7c48c3b3b18b064)
EN 1993-1-3 
to DIN 18800-2 
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
