Basically, there are two different calculation methods: the linear static analysis and the second-order analysis. As a special form of the calculation according to the second-order analysis, there is the large-deformation analysis available.
Basics of the Analytical Model
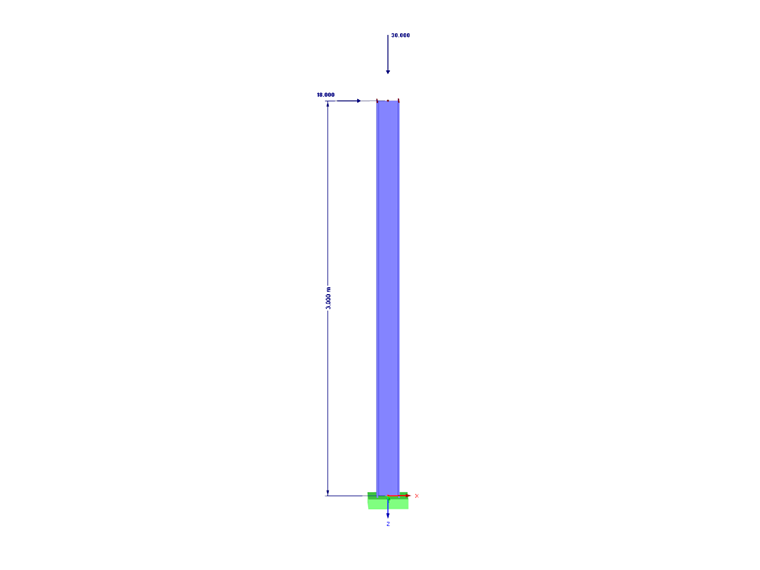
As a calculation example, there is a cantilever beam with a length of 3.0 m. The head load is 18 kN in the horizontal direction of the major axis and 30 kN in the vertical direction. The designed cross-section is HEA 180, made of S235 structural steel.
Calculation According to Linear Static Analysis
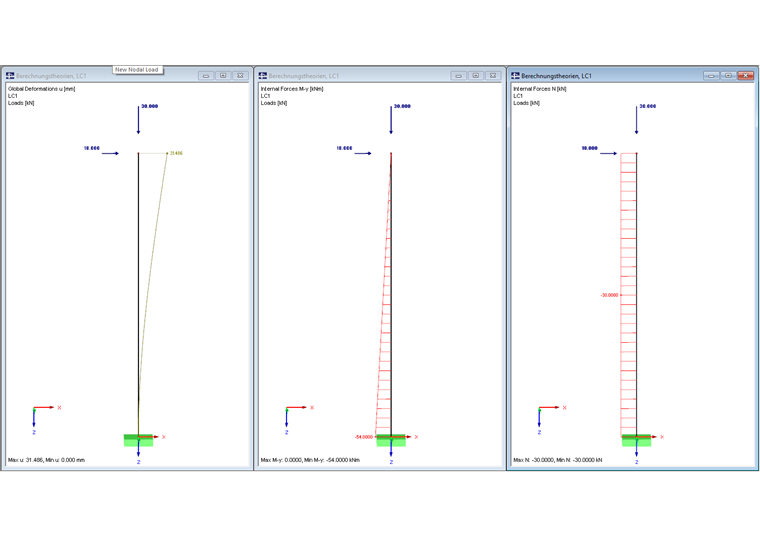
The calculation of internal forces according to the linear static analysis describes a linear calculation on an undeformed system. It is assumed that no deformations arise. In many cases of general structural analysis, this approach is sufficient.
The moment at the column base is calculated as follows:
Calculation According to Second-Order Analysis
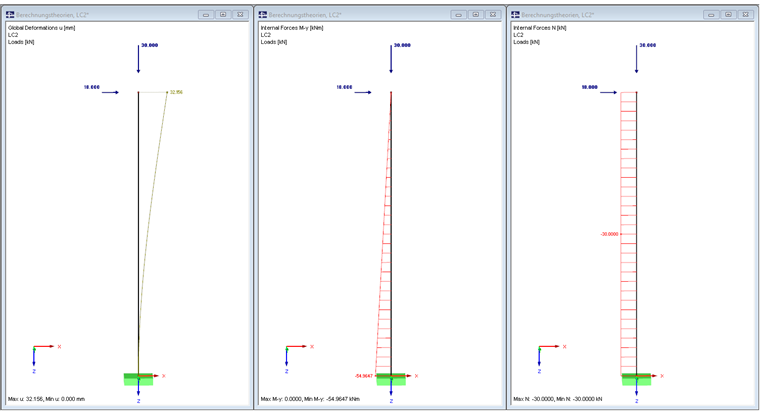
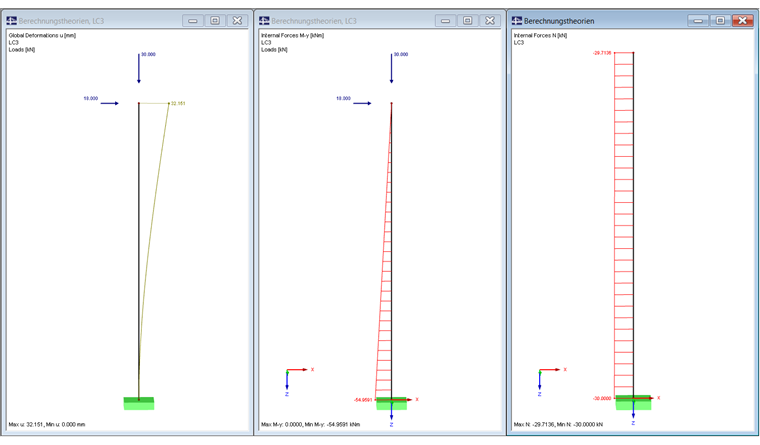
The calculation according to the second-order analysis describes a nonlinear calculation of the structure on a deformed system. This means that the deformations arising have an influence on the internal forces. The acting axial force additionally increases the moment on the support nodes of the column.
In this case, the moment is:
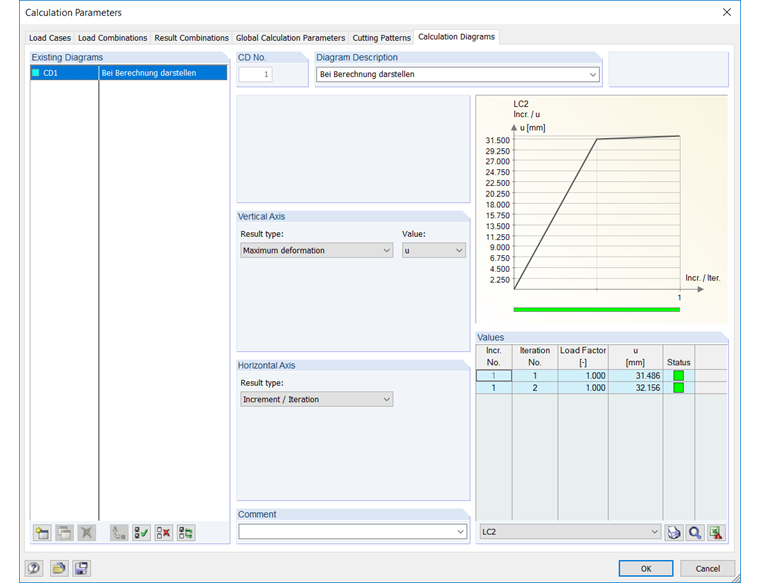
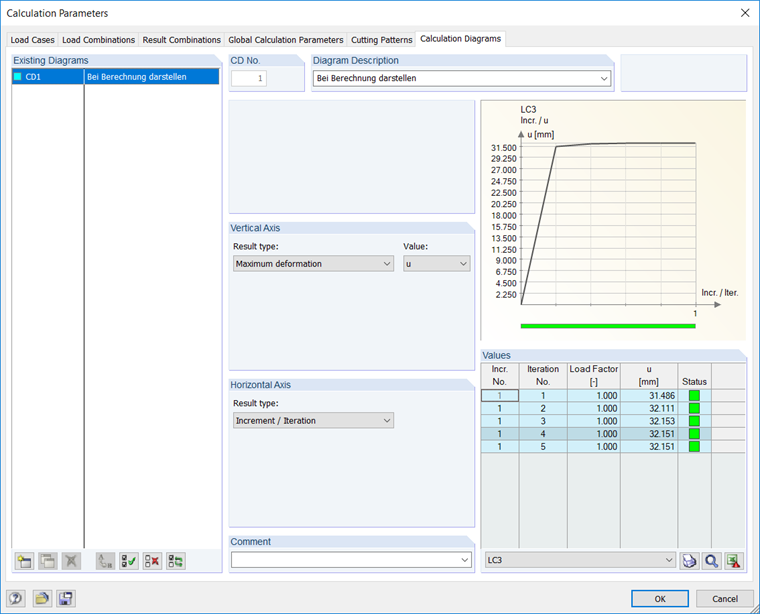
However, this analysis method assumes small deformations, since only deformations are considered, but no rotation of the structure. In the computational calculation, the linear analysis is used to determine the axial forces of the member, and in the second iteration, the additional moment is calculated from the deformation. The iteration diagram of RFEM reflects this behaviour.
The modification of internal forces N and V with respect to the deformation is not considered further, according to this calculation method. In RFEM, however, it is possible to convert the internal forces of the second-order analysis to the deformed structure, and thus perform the design.
Calculation According to Large Deformation Analysis
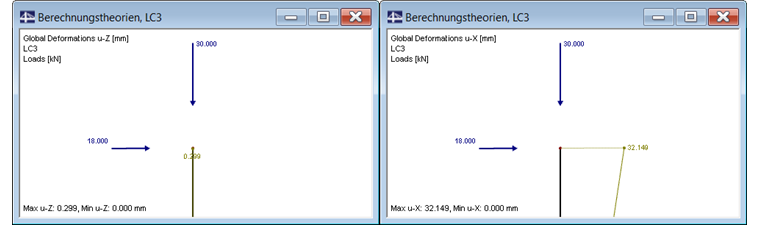
This calculation method also takes into account the rotation of the structure. It is a nonlinear calculation, like the second-order analysis. After each iteration step, the stiffness matrix of the deformed system is generated and the calculation continues until the equilibrium is reached.
The resulting moment at the column base is as follows:
A comparison of the member internal forces shows that the calculation according to the large deformation analysis also has an influence on the shear and axial forces of the structure.
Conclusion
The results of the different calculation methods show that the deformation does have an impact on the internal forces. In this case, the calculation according to the large deformation analysis seems to be the most accurate, but it also takes the most computing time. Moreover, some effects (torsional forces, etc.) may arise in the case of the large deformation analysis, causing difficulties in further design. Therefore, it is necessary to exactly check which calculation method is required for the given structure. In this case, you can follow the rule to perform the calculation "as simply as possible, but as accurately as necessary".