5723x

001650

Dipl.-Ing. (FH) Lukas Sühnel

2020-08-05

Determination of Resultant from FEM Model for Simplified Weld Design

The European standard EN 1993-1-8, Section 4.5.3.3. provides the user with a simplified method for the ultimate limit state design of fillet welds. According to the standard, the design is fulfilled if the design value of the resultant acting on the fillet weld area is smaller than the design value of the weld's load-bearing capacity. Thus, if you want to dimension the weld for a surface model, you will be faced with a variety of results due to the nature of FEM calculations. Therefore, we show in the following text how to determine the force components from the model.

The model of this technical article is based on the system of a gusset plate attached to a column, which is described in more detail on Page 8.67 in [1].

Structural System

Basically, the system consists of an HEB 140 column, to the flange of which a gusset plate is to be welded by means of a double fillet weld. This plate connects the column with a tension member, which should be ignored. The acting load is 330 kN and is allocated to the three bolt holes in the system. Although the load is known here, the required forces should be determined from the internal forces of the gusset plate. The load serves only for verification purposes.

1 System with Local Axis System of Gusset Plate

Determination of Resultant

The formula for the resultant is taken from Table 8.66c in [1].

F_{w, Ed} = \sqrt{({N^{2}}_{⊥, Ed} + {V^{2}}_{⊥, Ed} + {V^{2}}_{∥, Ed})}

Force Resultant

The individual force components can be calculated as follows.

N_{⊥, Ed} = \frac{F_{1 ⊥, Ed}}{l_{w}} \pm \frac{M_{Ed}}{(\frac{l_{w}^{2}}{6})}

V_{⊥, Ed} = \frac{F_{2 ⊥, Ed}}{l_{w}}

V_{∥, Ed} = \frac{F_{∥, Ed}}{l_{w}}

Force Components

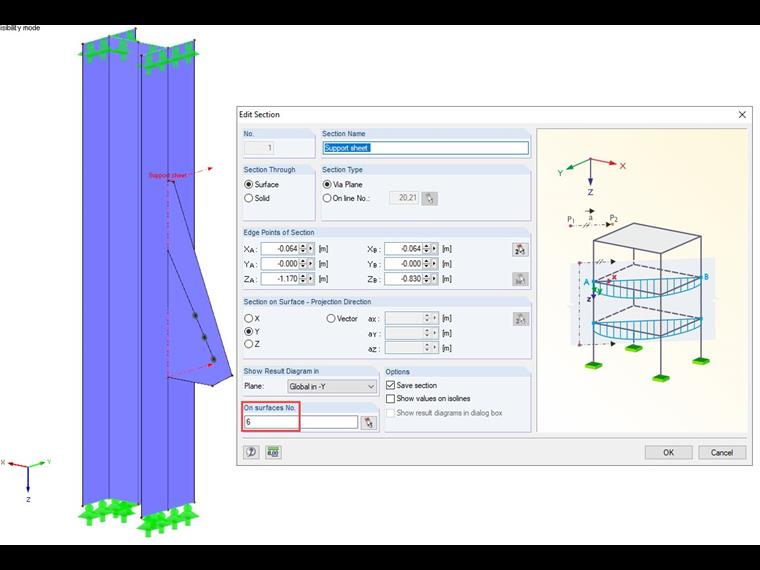
The forces F as well as the moment can be determined by defining a section. In the section dialog box, only the gusset plate should be considered.

2 Section Definition

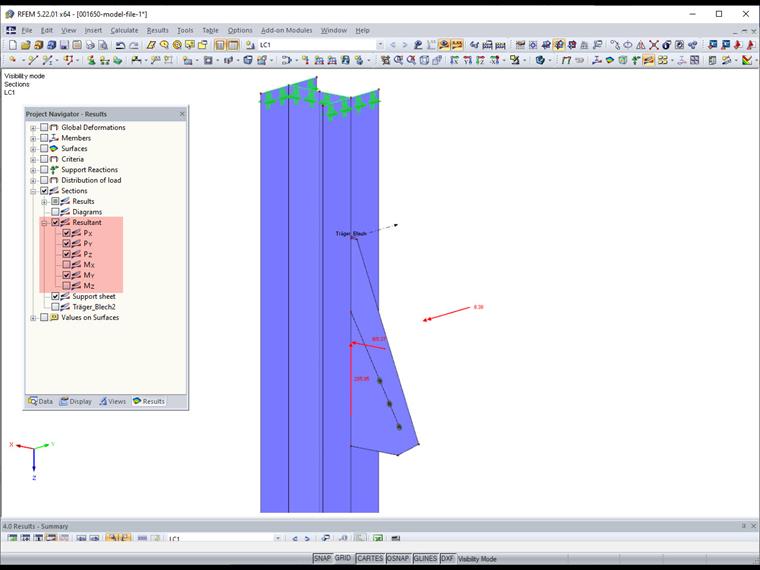
Method 1

After the calculation, you can graphically display the section resultants for each section.

3 Resultant Forces and Moments of Section

These values can now be inserted in the corresponding formulas. The assignment of the resultants to forces is as follows in this example.

F_1⊥,Ed = P_X = 165.37 kN
F_2⊥,Ed = P_Y = 0 kN
F_ll,Ed = P_Z = 285.95 kN
M_Ed = M_Y = 8.38 kNm

Since the section resultants are arranged analogously to the global axes, further result transformations would be necessary for welds or sections lying elsewhere, in order to get the corresponding forces and moments. Therefore, we show another method.

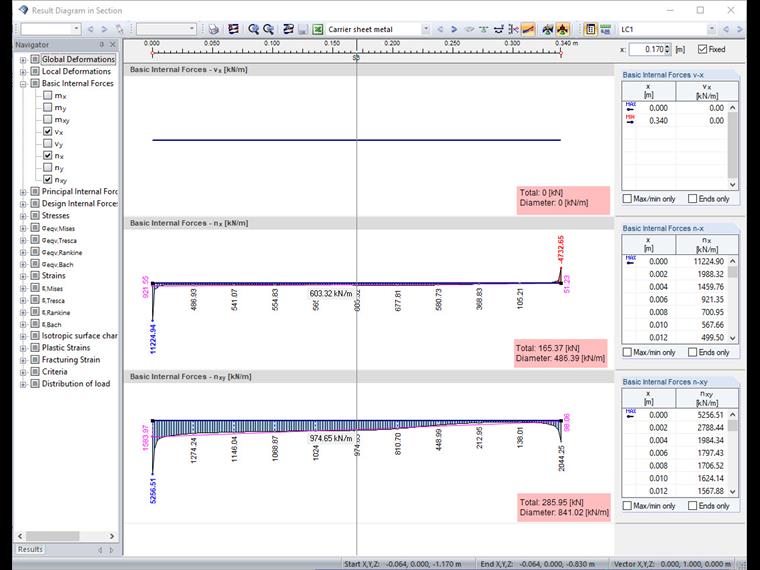
Method 2

Again, the section already created can be used. The corresponding result diagram is opened for further evaluation.

4 Resultant Forces and Moments of Section

Taking into account the local surface-axis system, the basic internal forces v_x (= 0 as there are no horizontal loads) and n_x as well as n_xy are represented. The result interpretation of the diagrams again provides the required forces. Another calculation is required only for the determination of the moment. For this, the intermediate values of the basic internal force n_x are exported to the Excel spreadsheet. Then, the moment results from the sum of the forces of the individual segments multiplied by the corresponding distance to the center of the section.

5 Result Values of Section

The results of both methods are identical. A mental check by decomposing the force of 330 kN acting at an angle of 30° also results in the force pairs and the moment of:
F_⊥,Ed = 330 ⋅ sin 30 ° = 165 kN
F_ll,Ed = 330 ⋅ cos 30 ° = 285 kN
M_Ed = 165 ⋅ 0.05 = 8.3 kNm

Design of Fillet Weld

The resultant can now be determined by means of the forces and the moment.
N_⊥,Ed = 165 / 34 + 8.38 / ( 34² / 6 ) = 9.20 kN/cm
V_⊥,Ed = 0
V_ll,Ed = 286 / 34 = 8.41 kN/cm
F_w,Ed = √ 9.2² + 8.41² = 12.46 kN/cm

Finally, this is compared to the design value of the ultimate limit state of the fillet weld. The fillet weld thickness is assumed to be 3 mm.

F_{w, Rd} = \frac{f_{u}}{\sqrt{3} \cdot β_{w} \cdot γ_{M 2}} \cdot 2 \cdot a_{w}

Design Value of Fillet Weld Resistance

F_w,Rd = ( 36 / √ 3 ⋅ 0.8 ⋅ 1.25 ) ⋅ 2 ⋅ 0.3 = 12.47 kN/cm
F_w,Ed = 12.46 kN/cm < F_w,Rd= 12.47 kN/cm

Knowledge Base

KB 001650 | Determination of Resultant from FEM Model for Simplified Weld Design

Author

Mr. Sühnel is responsible for the quality assurance of RSTAB; he also participates in product development and provides technical support for our customers.

Links

Structural Analysis Software for Steel Structures

References

Albert, A. (2020). Schneider - Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen, (24th ed.). Cologne: Reguvis.

Downloads

Determination Med | Excel file

60.14 KB

;