5720x

001650

Dipl.-Ing. (FH) Lukas Sühnel

5.8.2020

Stanovení výslednice sil z modelu MKP pro zjednodušené posouzení svaru

EN 1993-1-8 nabízí uživateli v článku 4.5.3.3 možnost posoudit únosnost svaru zjednodušenou metodou. Posouzení je v tomto případě splněno, pokud je návrhová hodnota výslednice sil působících na plochu svaru menší než návrhová hodnota únosnosti svaru. Pokud bychom chtěli svar dimenzovat pro plošný model, byli bychom z povahy výpočtů MKP konfrontováni se značným množstvím výsledků. Proto v našem článku ukážeme, jak lze stanovit složky sil z modelu.

Model v tomto odborném příspěvku je založen na systému styčníkového plechu připojeného ke sloupu, který je podrobněji popsán na straně 8.67 v [1].

Systém

V zásadě se tento systém skládá ze sloupu HEB 140, na jehož pásnici se má přivařit styčníkový plech dvojitým koutovým svarem. Tento plech spojuje sloup s tahovým prutem, který se ovšem nebude brát v potaz. Působící zatížení je 330 kN, které je rozděleno na tři otvory pro šrouby a dále přenášeno do systému. Ačkoli zatížení je zde známo, potřebné síly se stanoví z vnitřních sil styčníkového plechu. Zatížení nám bude sloužit pouze pro kontrolu.

1 System mit lokalem Achsensystem des Knotenbleches

Stanovení výslednice sil

Die Formel für die Kraftresultierende wird aus Tafel 8.66c in [1] entnommen.

F_{w, Ed} = \sqrt{({N^{2}}_{⊥, Ed} + {V^{2}}_{⊥, Ed} + {V^{2}}_{∥, Ed})}

Kraftresultierende

Jednotlivé složky sil lze spočítat následovně.

N_{⊥, Ed} = \frac{F_{1 ⊥, Ed}}{l_{w}} \pm \frac{M_{Ed}}{(\frac{l_{w}^{2}}{6})}

V_{⊥, Ed} = \frac{F_{2 ⊥, Ed}}{l_{w}}

V_{∥, Ed} = \frac{F_{∥, Ed}}{l_{w}}

Složky síly

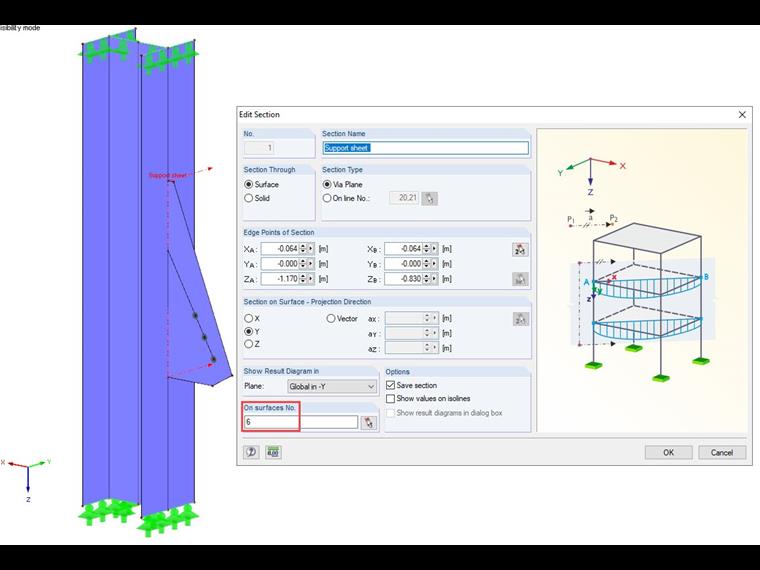
Síly F i moment můžeme určit ze zadaného řezu. Přitom se v dialogu řezu bude uvažovat pouze styčníkový plech.

2 Zadání řezu

Metoda 1

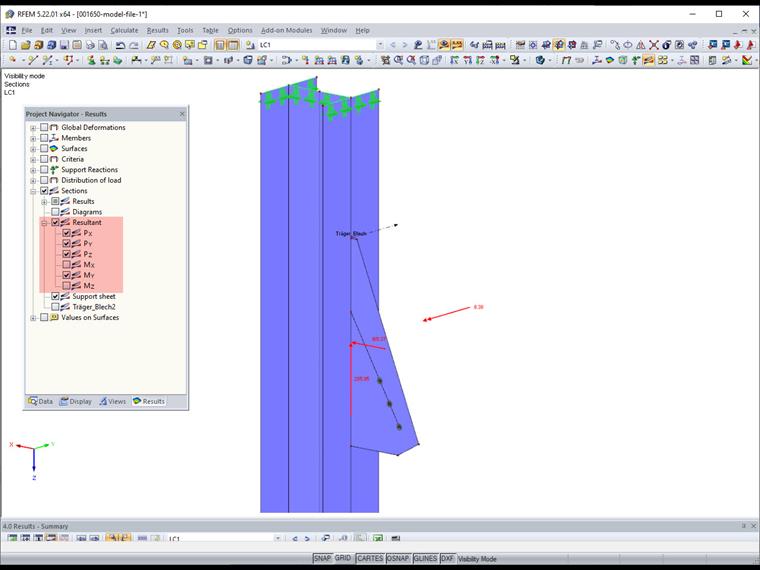
Po výpočtu si můžeme nechat zobrazit graficky výslednice pro každý řez.

3 Resultierende Kräfte und Momente des Schnittes

Tyto hodnoty lze nyní dosadit do příslušných vzorců. Výslednice se k silám přiřadí v našem příkladu následovně.

F_1⊥,Ed = P_X = 165, 37 kN
F_2⊥,Ed = P_Y = 0 kN
F_ll,Ed = P_Z = 285, 95 kN
M_Ed = M_Y = 8, 38 kNm

Protože výslednice na řezech jsou ustanoveny analogicky ke globálním osám, bylo by při jiném umístění svarů, respektive řezů nezbytné výsledky dále transformovat, abychom dostali odpovídající síly a momenty. Proto bychom si měli ukázat i jinou metodu.

Metoda 2

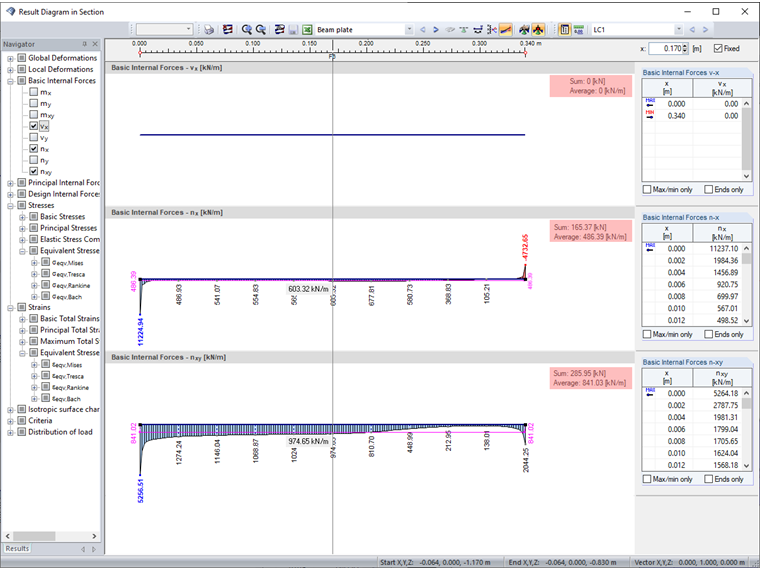
I v tomto případě můžeme použít již vytvořený řez. Pro další vyhodnocení si otevřeme příslušný průběh výsledků.

4 Resultierende Kräfte und Momente des Schnittes

Unter Beachtung des lokalen Flächen-Achsen-Systems werden die Grundschnittgrößen v_x (= 0, da keine horizontalen Lasten), n_x sowie n_xy dargestellt. Die Ergebnisinterpretation der Verläufe liefert erneut die benötigten Kräfte. Einzig für die Bestimmung des Momentes bedarf es einer weiteren Berechnung. Hierzu werden die Zwischenwerte der Grundschnittgröße n_x nach Excel exportiert. Das Moment ergibt sich dann aus der Summe der Kräfte der einzelnen Segmente multipliziert mit dem zugehörigen Abstand bis zur Mitte des Schnittes.

5 Ergebniswerte des Schnittes

Výsledky jsou v případě obou metod totožné. Pokud provedeme kontrolu rozložením síly 330 kN působící v úhlu 30° dostaneme také dvojice sil a moment:
F_⊥,Ed = 330 ⋅ sin 30 ° = 165 kN
F_ll,Ed = 330 ⋅ cos 30 ° = 285 kN
M_Ed = 165 ⋅ 0,05 = 8, 3 kNm

Posouzení koutového svaru

Na základě sil a momentu lze nyní určit výslednici sil.
N_⊥,Ed = 165 / 34 + 8, 38 / ( 34² / 6 ) = 9, 20 kN/cm
V_⊥,Ed = 0
V_ll,Ed = 286 / 34 = 8, 41 kN/cm
F_w,Ed = √ 9, 2² + 8, 41² = 12, 46 kN/cm

Tato hodnota se nakonec porovná s návrhovou únosností koutového svaru. Přitom se uvažuje tloušťka koutového svaru 3 mm.

F_{w, Rd} = \frac{f_{u}}{\sqrt{3} \cdot β_{w} \cdot γ_{M 2}} \cdot 2 \cdot a_{w}

Návrhová hodnota únosnosti koutového svaru

F_w,Rd = ( 36 / √ 3 ⋅ 0, 8 ⋅ 1, 25 ) ⋅ 2 ⋅ 0, 3 = 12, 47 kN/cm
F_w,Ed = 12, 46 kN/cm < F_w,Rd= 12, 47 kN/cm

Databáze znalostí

KB 001650 | Stanovení výslednice sil z modelu MKP pro zjednodušenou tíhu ...

Autor

Ing. Sühnel zajišťuje kvalitu programu RSTAB, podílí se na vývoji programů a poskytuje technickou podporu zákazníkům.

Odkazy

Software pro statické výpočty ocelových konstrukcí

Reference

Albert, A. Schneider - Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen, 24. vydání. Kolín nad Rýnem: Reguvis, 2020

Stahování

Stanovení Med | Soubor Excel

60,14 KB

;