Considérer des semi-rigidités entre des surfaces

Modèle réel et système structurel

Semi-rigidités entre les barres

Les semi-rigidités entre les barres sont définies lors de la modélisation à l'aide des articulations de barre. La définition est ici comparable à la condition de l’indétermination statique pour déterminer l’indétermination statique de la structure :
n = r + 3 m - 3 h - g ≥ 0
où :
r = réactions d'appui
m = barres
n = nœuds
h = articulations

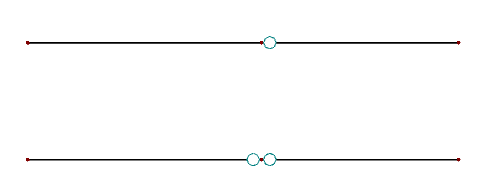
Il est donc nécessaire d'assigner toujours une articulation de moins que les barres avec le même degré de liberté (h = m - 1) au niveau d'un nœud. La Figure 02 montre une définition valide (en haut) et une définition non valide (en bas).

Articulation de barres, barres : correcte (en haut) et incorrecte (en bas)

Semi-rigidités entre les surfaces

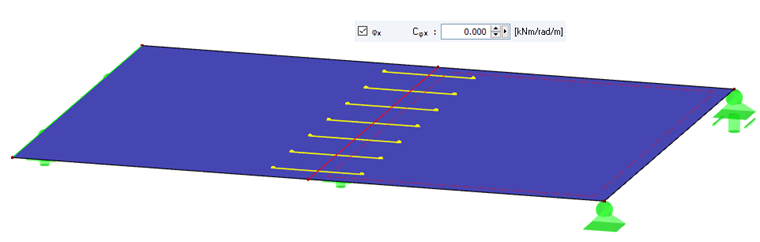
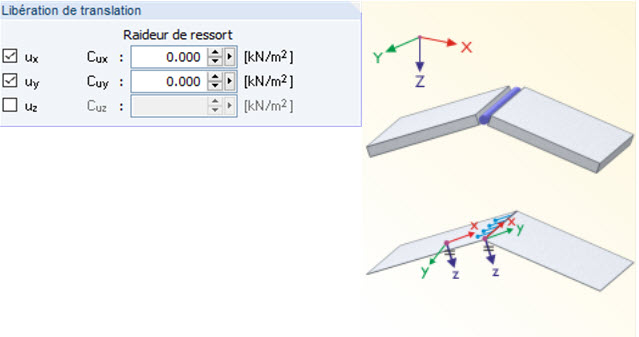
La définition des semi-rigidités entre les surfaces est plus complexe, mais repose sur les mêmes bases. Ici aussi, deux articulations génèrent une structure statique sous-déterminée avec un degré de liberté identique au niveau d'une ligne. Contrairement aux barres, les structures avec des surfaces ne sont pas instables aussi rapidement. Cela est dû en partie au fait que les surfaces peuvent se déformer dans leur plan et ne sont donc plus cinématiques. Fondamentalement, lors de la définition des articulations sur la Figure 03, la ligne tourne autour de son axe et la structure est donc cinématique.

Ligne cinématique résultant de deux articulations

Joint de séparation - Structures en béton

Le cas le plus simple d'articulations linéiques est le joint de séparation entre des surfaces en béton mentionné ci-dessus. Il est utilisé pour modéliser le joint de montage souvent nécessaire dans les structures en béton.
Pour cela, les articulations linéiques u_x, u_y et u_z sont libérées. Dans ce cas, nous recommandons de libérer également la rotation de la ligne. Dans le cas d'articulations, pour les barres comme les surfaces, le degré de liberté qui est libéré doit être sélectionné.

Assemblage d'un système structurel

Assemblage semi-rigide - Structures en bois

Dans les structures en bois, par exemple dans les structures en lamellé croisé ou les panneaux bois, la séparation entre les surfaces est généralement effectuée de manière semi-rigide. Il est assez facile de considérer un ressort linéaire entre deux surfaces à l'aide d'articulations linéiques. Cependant, le ressort des structures en bois n'est disponible que dans la direction de traction de la surface. Dans la zone de contact entre les surfaces, panneaux en bois ou murs en bois lamelé-croisé, une transmission de contact de pression quasi-rigide se produit. Cela complique significativement la modélisation pour ce type de semi-rigidité, car les propriétés non linéaires doivent être considérées.

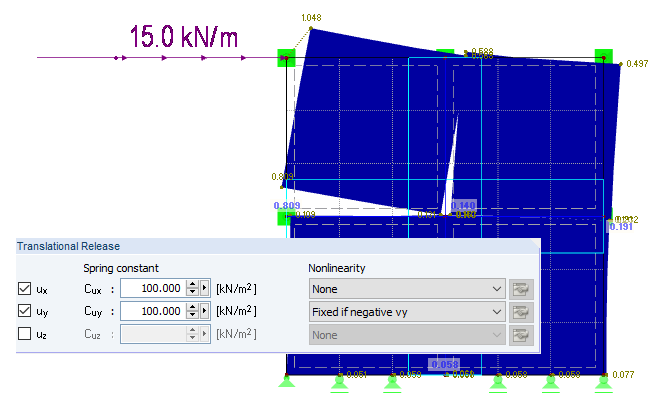
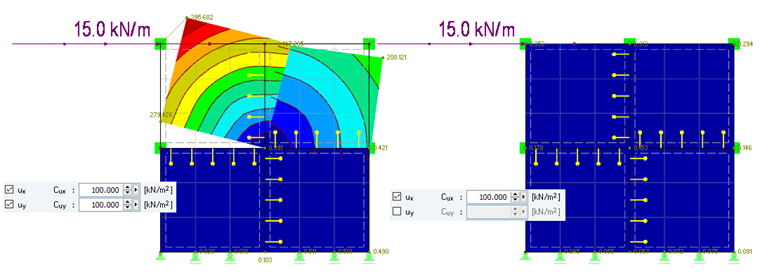
Les propriétés non linéaires présentent des désavantages pour ce qui est de la modélisation, l'évaluation des résultats, la durée du calcul, la quantité d'inconnues, etc. Il est expliqué ci-dessous comment considérer le contact de pression de non-linéarité avec les articulations linéiques. La Figure 05 montre une structure composée de quatre surfaces assemblées de manière semi-rigide. Au niveau du nœud d'appui, les modèles ont des appuis libres en u_x. À gauche, une surface est connectée de manière semi-rigide aux ressorts fictifs u_x = 100 kN/m² (direction longitudinale de la ligne) et u_y = 100 kN/m² (perpendiculaire à la ligne). À droite, la direction u_x = 100 kN/m² est connectée à l'identique. En u_y, la semi-rigidité est sélectionnée comme rigide. La charge horizontale est définie à 15 kN/m en tête.

Comparaison des rigidités

Comme le montre la Figure 05, la déformation du modèle de gauche est beaucoup trop élevée. De plus, les surfaces supérieures entre en intersection avec les surfaces inférieures. Cette déformation ne se produira pas ainsi en pratique. Cependant, la déformation du modèle de droite semble plausible. La Figure 06 montre la déformation de cisaillement n_xy entre les surfaces. La vérification des organes d'assemblage est effectuée pour cette valeur. Quelles que soient les valeurs, on constate que la déformation de cisaillement du modèle de gauche est toujours en rupture critique dans les deux sens (positif et négatif). Cela s'explique par le fait que les résultats des deux côtés de surface sont affichés et que les deux côtés considèrent la semi-rigidité au niveau de l'articulation. La contrainte de cisaillement diminue du centre vers le bord du modèle de droite. Cela résulte du chevauchement des rigidités à l'intérieur des surfaces assemblées.

Déformation de cisaillement nxy pour les articulations linéiques

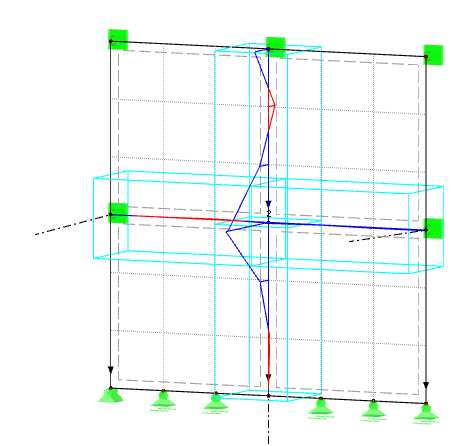
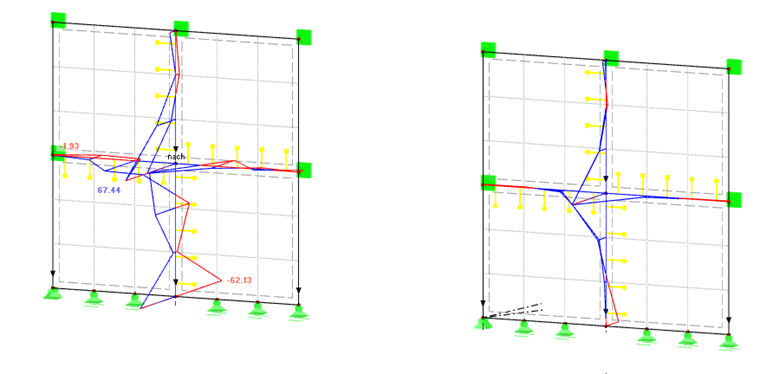
La Figure 07 montre l'effort dans une direction n_y. Les forces affichées sur les lignes font référence à l'orientation des axes de surface locaux.

Kräfte in ny-Richtung

La direction de la force est indiquée par des flèches en pointillés rouges et violettes sur la Figure 07. Le modèle de gauche présente une distribution des efforts normaux perturbée dans l'axe vertical, ce qui entraîne même une rupture post-critique du composant de traction dans la partie inférieure. Le modèle de gauche a des efforts de traction très élevées dans la direction y lorsque l'on regarde l'axe horizontal. L'incrément d'effort normal dans l'axe vertical commence à zéro et augmente au centre dans le modèle de droite. Les efforts dans l'axe horizontal sont très minimes. La distribution des efforts du modèle de droite est donc la plus plausible.

Théorie de la libération linéique et de l'articulation linéique

Pour considérer la non-linéarité, par exemple, dans le domaine de la transmission de contact de pression du modèle montré dans la section précédente, RFEM offre la possibilité de définir des libérations linéiques. Les bases théoriques sont les mêmes pour les articulations linéiques et les libérations linéiques. Les deux sont soumis à la technologie des deux nœuds. En définissant la libération, des nœuds virtuels doubles sont générés aux nœuds d'origine. Ces nœuds sont ensuite reliés entre eux par un ressort. Dès que des non-linéarités supplémentaires (par exemple un contact de pression) sont définies pour ce ressort, un alignement des déformations est effectué pour vérifier si la condition est remplie. Le terme technique pour cette méthode est la pénalisation. La Figure 08 en montre une vue schématique.

Méthode de la pénalisation [1]

Il est également possible d'effectuer un alignement en fonction de la force. La non-linéarité représentée sur la Figure 08 est contrôlée par les forces dans la direction correspondante. L'équation 1 montre une vue schématique du système d'équations pour la rigidité de pénalité k en N/m. Nous ne nous étendrons pas là-dessus dans cet article.

Équation 1 :

L'Équation 2 montre le système d'équations identique avec les multiplicateurs de Lagrange.

Équation 2 :

Les systèmes d'équations ne diffèrent en dernière partie que par le facteur λ. Il est clair que le calcul avec des multiplicateurs de pénalité ou de Lagrange donne des résultats identiques, du moins dans la première étape. Pour les structures plus complexes, il est préférable d'utiliser les multiplicateurs de Lagrange. Après la valeur de départ nulle, le schéma d'itération est étendu par les multiplicateur de Lagrange

Libération linéique

En définissant une libération linéique dans RFEM, il est possible de considérer complètement une non-linéarité pour l'exemple mentionné ci-dessus. Dans le cas du modèle actuel, une déformation comparable au modèle rigide avec les semi-rigidités en u_x émerge pour les semi-rigidités identiques de la non-linéarité contact de pression (Figure 09).

Déformations pour les libérations linéiques

Les efforts internes n_xy ont une distribution identique des efforts internes par rapport à la connexion verticale, comme le modèle avec une seule semi-rigidité (Figure 10). Seule la ligne horizontale change du côté droit du modèle car cette surface est complètement sous pression.

Distorsion de cisaillement pour les libérations linéiques

Définition du côté de surface

Indépendamment de la sélection d'une libération linéique ou d'une articulation linéique pour la définition de la semi-rigidité, il est important d'afficher correctement le modèle.

Modèle réel

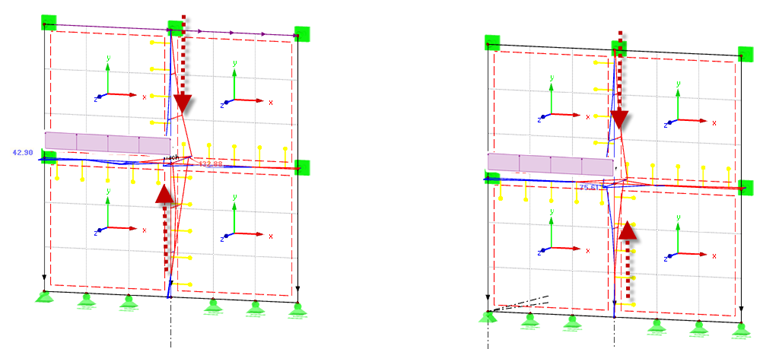
La Figure 11 montre le clouage avec panneau de couplage (à gauche) et encoche (à droite). La Figure 12 montre le modèle structural correspondant. Lors de la modélisation de la structure, il est important de définir la semi-rigidité en u_x , donc dans la direction longitudinale de l'assemblage, deux fois à gauche et une seule fois à droite. En raison de la loi de Hooke, le modèle de gauche a une double semi-rigidité.

Système statique

Résumé

Les semi-rigidités entre les surfaces peuvent être considérées dans RFEM à l'aide de l'option libération linéique ou articulation linéique. L'évaluation des résultats et la modélisation de la structure sont plus faciles pour le calcul avec des articulations linéiques. En contrepartie, l'utilisateur doit accepter, le cas échéant, des résultats moins précis. En plus de considérer la semi-rigidité entre les surfaces, la libération linéique permet également une situation d'appui non linéaire.