Klouby na koncích mezi pruty
Die Definition von Nachgiebigkeiten zwischen Stäben erfolgt in der statischen Modellierung mittels Stabendgelenken. Die Definition erfolgt hierbei vergleichbar zum Abzählkriterium zur Bestimmung der statischen Bestimmtheit eines Systems:
n = r + 3 s - 3 k - g ≥ 0
kde
r = Auflagerreaktionen
s = Stäbe
k = Knoten
g = Gelenke
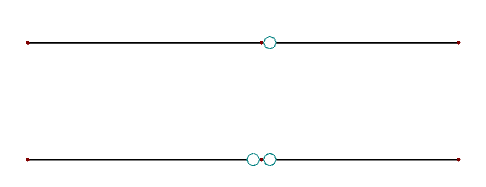
Demzufolge muss an einem Knoten immer ein Gelenk weniger als Stäbe mit dem gleichen Freiheitsgrad angeordnet werden (g = s - 1). In Bild 02 sind eine gültige Definition (oben) und eine ungültige Definition (unten) dargestellt.
Nachgiebigkeit zwischen Flächen
Die Definition von Nachgiebigkeiten zwischen Flächen ist komplexer, basiert aber auf identischen Grundlagen. Auch hier erzeugen zwei Gelenke mit identischem Freiheitsgrad an einer Linie ein statisch unterbestimmtes System. Im Unterschied zu Stäben werden die Systeme bei Flächen jedoch nicht so schnell instabil. Dies liegt unter anderem daran, dass Flächen sich in ihrer Ebene verwölben können und dadurch nicht mehr kinematisch sind. Prinzipiell wird sich aber bei der Definition der Gelenke in Bild 03 die Linie um ihre eigene Achse drehen und das System daher kinematisch werden.
Trennfuge - Betonbau
Der einfachste Fall der Liniengelenke ist die eingangs erwähnte Trennfuge zwischen Betonflächen. Hiermit wird die im Betonbau häufig notwendige Montagefuge modelliert.
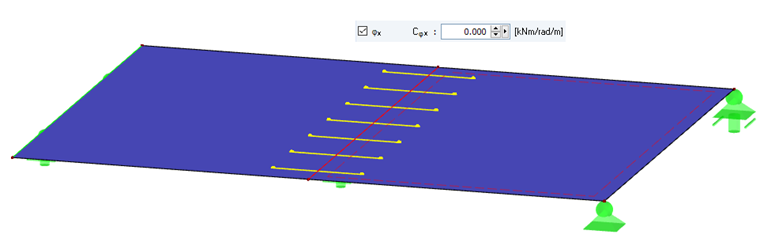
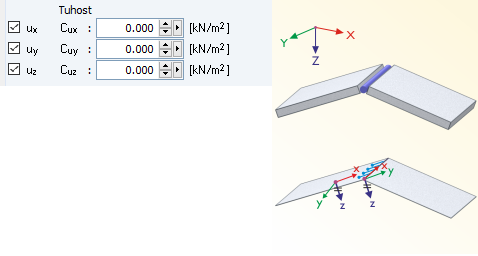
Hierfür werden die Liniengelenke in ux, uy und uz freigegeben (Bild 04). Die Rotation der Linie sollte für diesen Fall ebenfalls freigegeben werden. Bei Gelenken ist es sowohl bei Stäben als auch bei Flächen so, dass der Freiheitsgrad, der freigegeben wird, angewählt werden muss.
Nachgiebige Verbindung - Holzbau
Im Holzbau, zum Beispiel im Brettsperrholzbau oder Holztafelbau, erfolgt die Trennung zwischen Flächen üblicherweise nachgiebig. Eine lineare Feder zwischen zwei Flächen kann über Liniengelenke vergleichsweise einfach berücksichtigt werden. Allerdings ist die Feder im Holzbau eigentlich nur in Zugrichtung der Fläche gegeben. Im Kontaktbereich zwischen den Flächen beziehungsweise Holztafeln oder Brettsperrholzwänden ergibt sich eine nahezu starre Druckkontaktübertragung. Dies macht die Modellierung für derartige Nachgiebigkeiten sehr viel komplexer, da nichtlineare Eigenschaften berücksichtigt werden müssen.
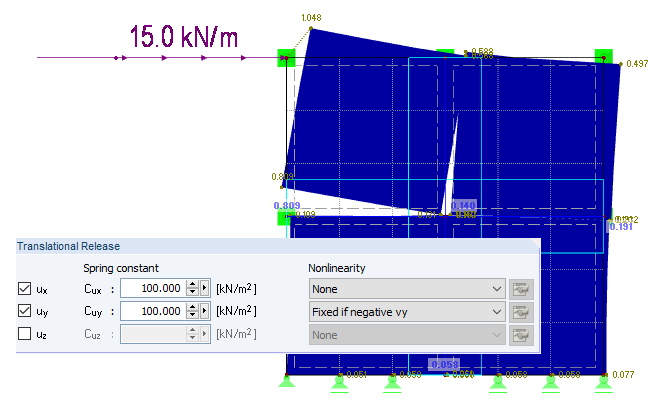
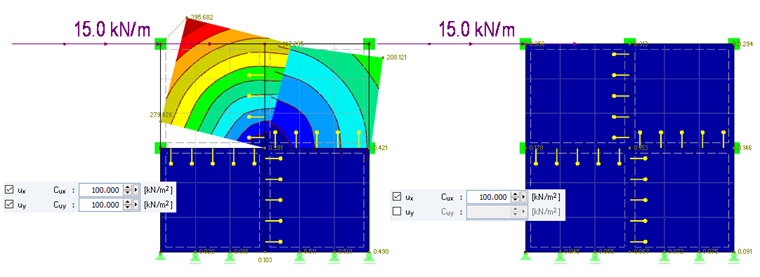
Nichtlineare Eigenschaften bedingen Nachteile in puncto Modellierung, Ergebnisauswertung, Berechnungsdauer, Anzahl der Unbekannten und so weiter. Im Folgenden wird erläutert, wie die Nichtlinearität Druckkontakt mit linearen Liniengelenken berücksichtigt werden kann. In Bild 05 ist ein System aus vier Flächen dargestellt, die nachgiebig miteinander verbunden sind. Am Fußpunkt sind die Modelle verschieblich in ux gelagert. Auf der linken Seite wird jeweils eine Fläche mit den fiktiven Federn ux = 100 kN/m² (Längsrichtung der Linie) und uy = 100 kN/m² (senkrecht zur Linie) nachgiebig verbunden. Auf der rechten Seite wird die Richtung ux = 100 kN/m² identisch angeschlossen. In uy wird die Nachgiebigkeit starr gewählt. Am Kopfpunkt wird eine horizontale Last von 15 kN/m definiert.
Wie in Bild 05 zu erkennen, ist die Verformung des linken Modells wesentlich zu hoch. Desweiteren durchdringen die oberen Flächen zusätzlich die unteren Flächen. Dieses Verformungsbild wird sich in der Praxis so nicht einstellen. Die Verformungsfigur des rechten Modells erscheint hingegen plausibel. In Bild 06 ist die Schubverzerrung nxy zwischen den Flächen dargestellt. Auf diesen Wert erfolgt die Bemessung der Verbindungsmittel. Unabhängig von den Werten ist erkennbar, dass die Schubverzerrung des linken Modells immer einen Durchschlag in beide Richtungen (positiv und negativ) aufweist. Dies rührt daher, dass die Ergebnisse beider Flächenseiten ausgegeben werden beziehungsweise beide Seiten am Gelenk die Nachgiebigkeit berücksichtigen. Am rechten Modell baut sich die Schubverzerrung von der Mitte zum Rand hin ab. Dies liegt an der Überlappung der Steifigkeiten im inneren Bereich der angeschlossenen Flächen.
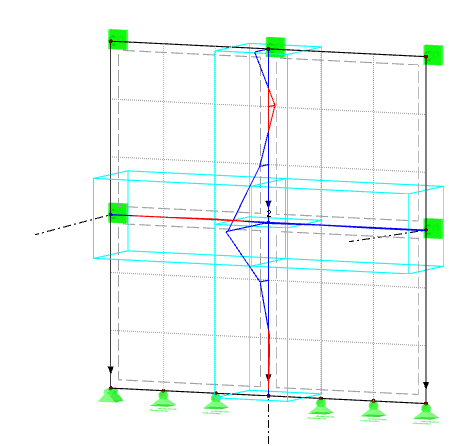
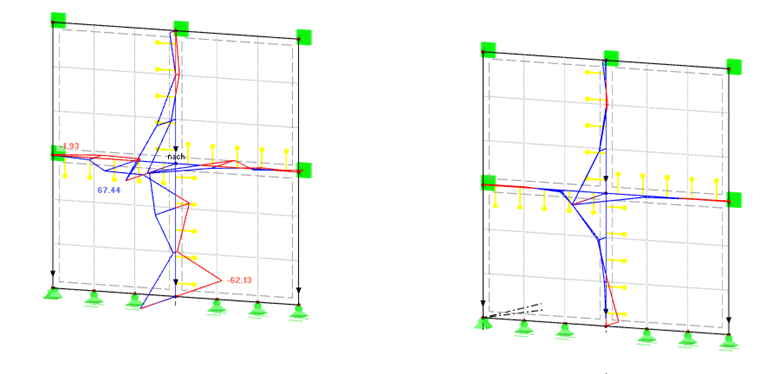
In Bild 07 ist die Kraft in ny-Richtung dargestellt. Die an den Linien ausgegebenen Kräfte beziehen sich jeweils auf die Orientierung der lokalen Flächenachsen.
Die Kraftrichtung wird in Bild 07 mit den gestrichelten roten und violetten Pfeilen gekennzeichnet. Für das linke Modell ergibt sich in vertikaler Achse ein gestörter Normalkraftverlauf, der im unteren Bereich sogar mit einer Zugkomponente durchschlägt. In horizontaler Achse ergeben sich beim linken Modell sehr hohe Zugkräfte in y-Richtung. Im rechten Modell ist der Normalkraftzuwachs in vertikaler Achse von Null zunehmend zur Mitte. In horizontaler Achse sind die Kräfte sehr minimal. Der Kräfteverlauf des rechten Models erscheint daher am plausibelsten.
Theorie Linienfreigabe und Liniengelenk
Um die Nichtlinearität, beispielsweise im Bereich der Druckkontaktübertragung, des im vorigen Abschnitt gezeigten Modells zu berücksichtigen, gibt es in RFEM die Möglichkeit der Definition von Linienfreigaben. Die theoretischen Grundlagen für Liniengelenke und Linienfreigaben sind dabei identisch. Beide unterliegen der sogenannten Doppelknotentechnologie. Dabei werden durch die Definition der Freigabe virtuelle doppelte Knoten an den ursprünglichen Knoten erzeugt. Diese Knoten werden dann über eine Feder miteinander verbunden. Sobald zusätzliche Nichtlinearitäten (zum Beispiel Druckkontakt) an dieser Feder definiert werden, wird über einen Verformungsabgleich untersucht, ob die Bedingung eingehalten ist. Der Fachbegriff unter dem diese Methode in der Literatur zu finden ist, nennt sich Penalty-Methode. In Bild 08 ist dies schematisch dargestellt.
Alternativ kann der Abgleich kraftbasiert erfolgen. Die in Bild 08 gezeigte Nichtlinearität wird dann über Kräfte in der jeweiligen Richtung kontrolliert. In Gleichung 1 ist schematisch das Gleichungssystem für die Penalty-Steifigkeit k in N/m dargestellt. Auf die weitere Herleitung sowie Erläuterung des zugrunde liegenden Systems wird in diesem Beitrag verzichtet.
Rovnice 1:
In Gleichung 2 wird das identische Gleichungssystem mit Lagrange-Multiplikatoren dargestellt.
Rovnice 2:
Die Gleichungssysteme unterscheiden sich lediglich im hinteren Term um den Faktor λ. Anhand dessen ist klar, dass die Berechnung mit Penalty- oder Lagrange-Multiplikatoren zumindest im ersten Schritt zu identischen Ergebnissen führt. Bei komplexeren Systemen konvergiert der Abgleich mittels Lagrange-Multiplikatoren jedoch besser. Das Iterationsschema wird nach dem Startwert Null um die Lagrange-Multiplikatoren erweitert
.Liniové uvolnění
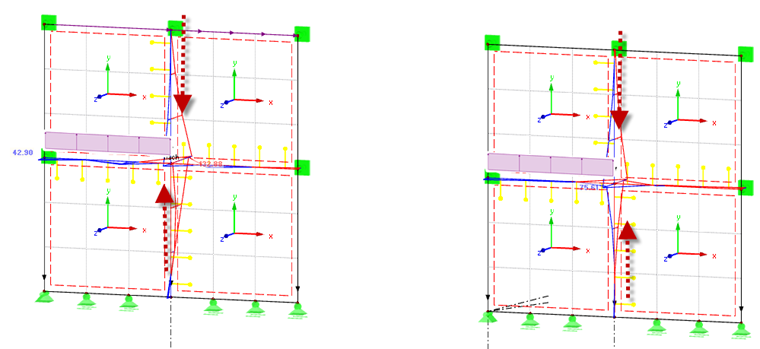
Eine vollumfängliche Berücksichtigung der Nichtlinearität für das eingangs angeführte Beispiel kann in RFEM mit der Definition einer Linienfreigabe erfolgen. Für das hier behandelte Beispiel ergibt sich bei identischer Nachgiebigkeit der Nichtlinearität Druckkontakt eine vergleichbare Verformungsfigur wie beim starren Modell mit Nachgiebigkeit in ux (Bild 09).
Die Schnittgrößen nxy zeigen bezogen auf die vertikale Verbindung qualitativ einen identischen Schnittgrößenverlauf wie das Modell mit nur einer Nachgiebigkeit (Bild 10). Lediglich die horizontale Linie ändert sich auf der rechten Seite des Modells, da diese Fläche komplett überdrückt wird.
Definition der Flächenseite
Unabhängig davon, ob eine Linienfreigabe oder ein Liniengelenk zur Definition der Nachgiebigkeit gewählt wird, ist es wichtig, das Modell statisch korrekt abzubilden.
In Bild 11 ist die Vernagelung mit Kopplungsbrett (links) und mit Falz (rechts) dargestellt. Bild 12 zeigt das zugehörige statische System. In der Modellierung ist es wichtig, hier die Nachgiebigkeit in ux, also in Längsrichtung der Verbindung, links zweimal zu definieren und rechts nur einmal. Aufgrund des Federgesetzes erhält das linke Modell die doppelte Nachgiebigkeit.
Závěr
Nachgiebigkeit zwischen Flächen kann in RFEM über die Option Linienfreigabe oder Liniengelenk berücksichtigt werden. Die Berechnung mittels Liniengelenk ist einfacher im Hinblick auf die Ergebnisauswertung und Modellierung des Systems. Dafür muss der Anwender gegebenenfalls ungenauere Ergebnisse in Kauf nehmen. Zusätzlich zur Berücksichtigung der Nachgiebigkeit zwischen Flächen beinhaltet die Linienfreigabe auch die Möglichkeit der Freigabe von Stäben an Flächen.

![Penalizační metoda [1]](/cs/webimage/009048/505809/08-de.png)