Esempio
Sono disponibili i seguenti casi di carico:
LC1 - Peso proprio
LC2 - Neve
LC3 - Carico imposto - alternativa 1
LC4 - Carico imposto - alternativa 2
Stiamo cercando l'inviluppo delle forze interne per SLU secondo EN 1990. I casi di carico imposti possono essere presi in considerazione nella combinazione.
Combinazione tramite combinazioni di risultati
Secondo EN 1990, Eq. 6.10, le azioni dovrebbero essere dotate di coefficienti di sicurezza parziali e coefficienti di combinazione. Tuttavia, è possibile specificare solo un coefficiente quando si definisce una combinazione di risultati. Pertanto, se non è chiaro quale azione variabile sia quella determinante, è necessario creare diverse combinazioni di azioni.
Dopo aver assegnato i coefficienti, è necessario definire un criterio e un gruppo. Le forze interne del peso proprio dovrebbero sempre essere applicate e sono quindi definite come permanenti. Possono verificarsi altri casi di carico, ma non necessariamente. Pertanto, in questo caso, il criterio variabile è assegnato. Le specifiche dei casi di carico imposti che agiscono alternativamente sono controllate dal gruppo. Entrambi i casi di carico imposti hanno lo stesso numero. Pertanto, per la combinazione viene utilizzato solo un caso di carico imposto.
La combinazione di risultati di inviluppo finale è generata come segue:
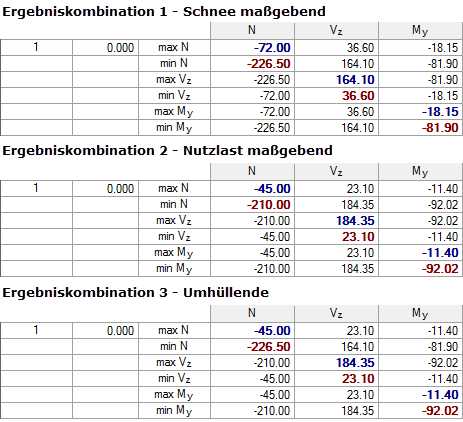
RC3 (ULS) = RC1/s o RC2/s
Sulla base di questo esempio teorico, ci sono le seguenti forze interne per RC1 e RC2 e le forze interne risultanti per RC3:
Combinazione tramite combinazioni di carico
Gli stessi quattro casi di carico saranno ora sovrapposti utilizzando le combinazioni di carico. Al fine di garantire che si trovino le forze interne più sfavorevoli, vengono create tutte le possibili combinazioni. Questi sono generati anche per quanto riguarda i carichi prevalentemente variabili e gli effetti alternativi dei carichi imposti. Il requisito di base per il successivo confronto con le combinazioni di risultati è un sistema lineare e il calcolo delle combinazioni di carico secondo l'analisi statica lineare.
Sono necessarie un totale di otto combinazioni di carico. Per confrontare i risultati con quelli delle combinazioni di risultati, viene creato un altro inviluppo RC, che include i risultati delle combinazioni di carico:
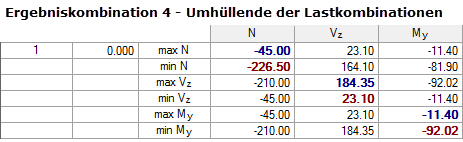
RC4 = CO1/p o CO2/p o CO3/p o CO4/p o CO5/p o CO6/p o CO7/p o CO8/p
Sulla base dello stesso sistema, otteniamo le seguenti forze interne:
Confronto dei risultati
Se si confrontano le forze interne di RC3 e RC4, in questo esempio non ci sono differenze. È interessante notare, tuttavia, che è necessario creare un totale di nove combinazioni (8 CC + 1 RC) nel caso della soluzione che utilizza combinazioni di carico, mentre la soluzione che utilizza la combinazione di risultati richiede solo tre combinazioni. Questo effetto di risparmio ha un'influenza positiva sul tempo di calcolo, nonché sulla panoramica nel programma e in particolare nella relazione.
Sommario
Nei modelli geometricamente lineari, che possono essere calcolati secondo l'analisi statica lineare, le combinazioni di risultati rappresentano uno strumento efficace per combinare i casi di carico. Può essere particolarmente utile quando si analizza una struttura con un gran numero di casi di carico (carichi di movimento, ad esempio), che altrimenti porterebbero a un numero elevato di combinazioni di carico e quindi renderebbero poco chiara la documentazione.