Основы

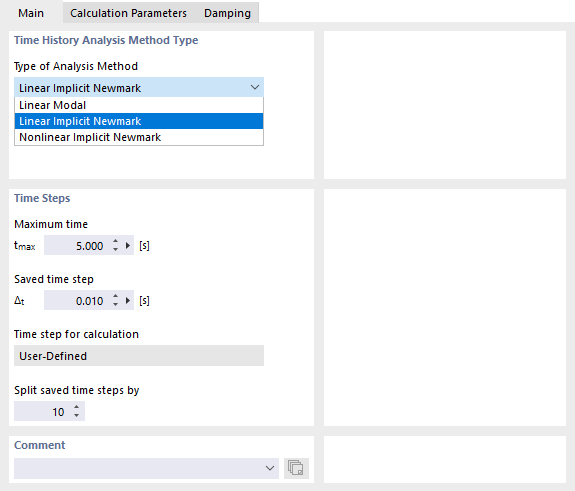
Регистр База управляет параметрами для метода и временных шагов.

Становление метода расчёта и временных шагов

Тип метода анализа по временным историям

В программе RFEM в списке доступны два линейных и один нелинейный метода анализа (см. рисунок Определение методов анализа и временных шагов):

• Линейный модальный
• Линейный имплицитный метод Ньюмарка
• Нелинейный имплицитный метод Ньюмарка

В RSTAB список содержит два линейных и два нелинейных метода анализа:

• Линейный модальный
• Линейный имплицитный метод Ньюмарка
• Нелинейный явный | I порядок
• Нелинейный явный | III порядок

Первые два метода анализа геометрически линейны, поэтому они применимы только для небольших деформаций. Кроме того, все нелинейные свойства модели либо игнорируются (например, не учитывается отказ опоры), либо заменяются (тяговый элемент представляется фермой).

Линейный модальный метод анализа использует раздельную систему, основанную на собственных значениях и формах модели, и определяется в присвоенном Загрузочном случае модального анализа . Многомассовая система ("MDOF") разлагается на множество одномассивных систем ("SDOF") (диагонализированная матрица масс и жесткости). Для обеспечения точности требуется определенное количество собственных значений. Решение для раздельной системы определяется с помощью имплицитного решателя уравнений Ньюмарка. Настройки матрицы масс и изменений жесткости переносятся из присвоенного загрузочного случая модального анализа. Если собственные значения уже определены, этот метод анализа несколько быстрее, чем линейный имплицитный метод Ньюмарка.

Линейный имплицитный метод Ньюмарка является методом прямой временной интеграции. Он требует достаточно малых временных шагов для получения точных результатов. Для этого метода анализа не требуется анализ на собственные колебания. Теоретические основы, например, изложены в [1]. В имплицитных методах неизвестные значения времени i + 1 определяются на основе значений времени i и i + 1. Необходимо решить нелинейные уравнения; итерации и контроль сходимости не требуются.

Нелинейный имплицитный метод Ньюмарка учитывает геометрические и конструктивные нелинейности модели. Метод безусловно устойчив: нет верхнего предела устойчивости во временном шаге Δt. Тем не менее, для точных результатов требуются достаточно малые временные шаги. Временной интервал зависит от возбуждения, частоты модели и сложности нелинейностей. Нет ограничений для матрицы масс и демпфирования Рэйли.

Нелинейный явный метод в RSTAB использует центрально-разностный метод. Он подходит для возбуждений короткой продолжительности и быстро меняющихся нелинейностей в модели. Метод однозначен, так как неизвестные значения зависят только от времени i и не от неизвестного ответа на время i + 1. Явное интеграционное правило хорошо работает в сочетании с диагональной матрицей масс и с ограничением матрицы демпфирования C = αM. Метод условно устойчив: ограниченное решение достигается только тогда, когда временной интервал Δt меньше стабильного временного интервала Δt_стабил. Предел стабильности может быть определен по наибольшему собственному значению модели ω_макс и доле критического демпфирования D на наибольшей собственной форме.

Для практики стабильный временной интервал может быть определен с помощью следующей оценки:

Скорость дилатационных волн для линейно упругого материала (с коэффициентом поперечной деформации равным нулю) определяется:

Эта оценка позволяет использовать меньшие временные шаги по сравнению с точным пределом стабильности. Однако следует учитывать, что многие эффекты не охвачены и из-за точности может потребоваться меньший временной шаг Δt. Программа использует постоянный временной шаг – стабильный начальный временной интервал или заданное пользователем значение.

Временные шаги

Укажите 'Максимальное время' t_макс, которое должно быть исследовано в расчетах. Затем установите в поле 'Сохраняемый временной шаг' интервал, в котором будут сохранятся результаты Δ_t. Результаты будут доступны только для этих временных шагов. Динамическая оболочка также формируется из сохраненных временных шагов.

Кроме временных шагов, которые сохраняются, необходимо установить временные шаги для фактических расчетов. Для этого введите значение в поле 'Сохраняемые временные шаги, разделенные на' для разделения сохраняемых временных шагов Δ_t.

Для успешного анализа по временным историям временные шаги должны быть выбраны "адекватно". В конечном итоге решение является компромиссом между временем вычислений и точностью. Для линейного анализа по временным историям можно дать следующую рекомендацию (см. [2]):

• С учетом акселерограммы и временных диаграмм переходных процессов, самая короткая длина дискретного возбуждения должна быть разделена на минимум семь временных шагов.
• Для вычисления временного шага следует использовать высшую частоту f модели, которая имеет значение для ответа системы, как показано здесь: Δt ≤ 1 / (20f). Аналогично, следует проверить, охватывается ли самая высокая частота возбуждения условием Δt ≤ 𝜋 / (10ω). Если это не так, временной шаг должен быть скорректирован.