Back to Online Manuals
146x
004102
Stine Effler, M.Sc.
2024-01-05
Overview
Add-ons for Dynamic Analysis
Modal Analysis
Response Spectrum Analysis
Harmonic Response Analysis
Time History Analysis
Pushover Analysis
Documentation

Main

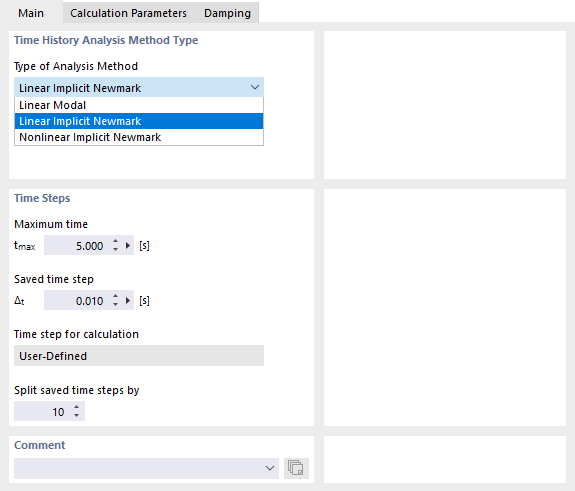
The Main tab manages the specifications for the method and the time steps.

Defining Analysis Method and Time Steps
Defining Analysis Method and Time Steps

Time History Analysis Method Type

Two linear time history analysis methods are available for selection in the list in this dialog section (see the image Defining Analysis Method and Time Steps):

  • Linear Modal
  • Linear Implicit Newmark

Both analysis methods are geometrically linear, so they are only valid for small deformations. Furthermore, all nonlinear properties of the model are either ignored (for example, the failure of a support is not considered) or replaced (a tension member is represented by a truss).

The linear modal analysis method uses a decoupled system that is based on the model's eigenvalues and mode shapes, and is determined in the assigned Modal Analysis Load Case . The multi-degree-of-freedom system ("MDOF") is split into many single-degree-of-freedom systems ("SDOF") (diagonalized mass and stiffness matrix). A certain number of eigenvalues is required to ensure accuracy. The solution of the decoupled system is then determined with an implicit (Newmark) solver. The mass matrix settings and stiffness modifications are taken from the assigned modal analysis load case. If the eigenvalues have already been determined, this analysis method is slightly faster than the linear implicit Newmark analysis.

The linear implicit Newmark analysis is a direct time integration method. It requires sufficiently small time steps to achieve precise results. No natural vibration analysis is required for this analysis method. The theoretical background is explained in [1], for example.

Important

If you want to use members of the Damper type with defined damping coefficients, select the Linear Implicit Newmark analysis method.

Time Steps

Enter the "Maximum time" tmax to be analyzed in the calculation. In the "Saved time step" text box, specify the interval Δt where the results should be saved. Results will only be available for these time steps. The dynamic envelope is also generated from the saved time steps.

Info

Fewer saved time steps reduce the file size and the calculation time. They also have a positive impact on the result evaluation. Nevertheless, a certain amount of result values is required in order to avoid exceeding the maximum and to generate uniform gradients for the calculation diagrams.

In addition to the time steps saved, it is necessary to define time steps for the actual calculation. To do this, enter a value in the "Split saved time steps by" text box that should divide the saved time steps Δt.

For a successful time history analysis, you need to select the time steps "appropriately". In essence, the decision represents a compromise between calculation time and accuracy. The following recommendation can be made for the linear time history analysis (see [2]):

  • Taking into account the accelerogram and the transient time diagrams, the shortest length of the discrete excitation should be divided into at least seven time steps.
  • To calculate the time step, the highest frequency f of the model that is relevant for the system response should be used as follows: Δt ≤ 1 / (20f). Similarly, you should check whether the highest frequency of the excitation is covered in the condition Δt ≤ 𝜋 / (10ω). If not, it is necessary to adjust the time step.
References
  1. Chopra, A.K. (2020). Dynamics of Structures – Theory and Applications to Earthquake Engineering. Prentice Hall.
  2. Stelzmann, U., Groth, C., & Müller, G. (2008). FEM für Praktiker – Band 2: Strukturdynamik. Expert-Verlag, Renningen-Malmsheim.
Parent Chapter