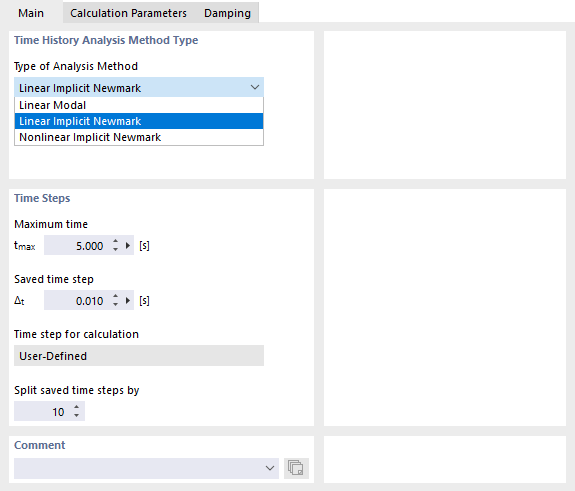
L’onglet Général permet de gérer les paramètres par défaut pour la méthode et les pas de temps.
Type de méthode d’analyse de l’historique de temps
Dans le logiciel RFEM, la liste propose deux méthodes d’analyse linéaire et une méthode non linéaire (voir l'image Définir les méthodes d'analyse et les pas de temps) :
- Modale linéaire
- Analyse linéaire implicite de Newmark
- Analyse non linéaire implicite de Newmark
Dans RSTAB, la liste comprend deux méthodes d’analyse linéaire et deux non linéaires :
- Modale linéaire
- Analyse linéaire implicite de Newmark
- Non linéaire explicite | Géométriquement linéaire
- Non linéaire explicite | Grandes déformations
Les deux premières méthodes d’analyse sont géométriquement linéaires, ce qui signifie qu’elles ne sont applicables que pour de petites déformations. De plus, toutes les propriétés non linéaires du modèle sont soit ignorées (par exemple, la défaillance d’un appui n’est pas prise en compte) ou remplacées (une barre de traction est modélisée par une barre en treillis).
La méthode d'analyse modale linéaire utilise un système découplé basé sur les valeurs propres et les modes propres du modèle déterminés dans le cas de charge d’analyse modale assigné. Le système à degrés de liberté multiples (« MDOF ») est décomposé en plusieurs systèmes à un degré de liberté (« SDOF ») (matrice de masse et de raideur diagonalisées). Un certain nombre de valeurs propres est requis pour garantir l’exactitude. La solution du système découplé est ensuite déterminée avec un solveur d’équation implicite de Newmark. Les paramètres de la matrice de masse et les modifications de raideur sont reprises du cas de charge d’analyse modale assigné. Si les valeurs propres sont déjà déterminées, cette méthode d’analyse est légèrement plus rapide que l’analyse implicite linéaire de Newmark.
L’analyse linéaire implicite de Newmark est une méthode d'intégration temporelle directe. Elle nécessite des pas de temps suffisamment petits pour obtenir des résultats précis. Cette méthode d’analyse ne nécessite pas d’analyse des fréquences propres. Les principes théoriques sont décrits par exemple dans [1]. Avec les méthodes de résolution implicites, les valeurs inconnues au temps i + 1 sont déterminées sur la base des valeurs aux temps i et i + 1. Des équations non linéaires doivent alors être résolues, aucune itération, ni contrôle de convergence ne sont requis.
L’analyse non linéaire implicite de Newmark prend en compte les non-linéarités géométriques et structurelles du modèle. Cette méthode est inconditionnellement stable : il n’y a pas de limite supérieure de stabilité dans le pas de temps Δt. Pour obtenir des résultats exacts, des pas de temps suffisamment petits restent requis. Le pas de temps est fonction de l’excitation, de la fréquence du modèle et de la complexité des non-linéarités. Il n’y a aucune restriction concernant la matrice de masse et l’amortissement de Rayleigh.
La méthode explicite non linéaire dans RSTAB utilise la méthode des différences centrales. Elle convient pour des excitations de courte durée et des non-linéarités rapidement changeantes dans le modèle. La méthode est explicite, car les valeurs inconnues sont basées uniquement sur le temps i et non sur la réponse inconnue au temps i + 1. La règle d’intégration explicite fonctionne bien en combinaison avec une matrice de masse diagonale et avec la restriction de la matrice d’amortissement C = αM. La méthode est conditionnellement stable : une solution limitée n’est obtenue que si le pas de temps Δt est inférieur au pas de temps stable Δtstable. La limite de stabilité peut être définie à partir de la plus grande valeur propre du modèle ωmax et de la composante d’amortissement critique D dans le mode propre le plus important.
En pratique, le pas de temps stable peut être déterminé avec l’estimation suivante :
La vitesse des ondes de dilatation pour un matériau élastique linéaire (avec un coefficient de Poisson égal à zéro) est calculée comme suit :
Cette estimation permet des pas de temps plus petits par rapport à la limite de stabilité exacte. Toutefois, il convient de noter que de nombreux effets ne sont pas pris en compte dans cette estimation et, par souci de précision, un pas de temps plus petit Δt peut être requis. Le logiciel utilise une largeur de pas de temps fixe – soit le pas de temps initial stable, soit une valeur définie par l’utilisateur.
Pas de temps
Indiquez le « Temps maximal » tmax à examiner lors du calcul. Définissez ensuite dans le champ « Pas de temps enregistré » l’intervalle Δt auquel les résultats doivent être enregistrés. Les résultats ne sont disponibles que pour ces pas de temps. L’enveloppe dynamique est également constituée des pas enregistrés.
En plus des pas de temps à enregistrer, des pas pour le calcul doivent être définis proprement dit. Pour cela, entrez une valeur par laquelle les pas enregistrés Δt doivent être divisés dans le champ « Diviser les pas enregistrés par ».
Pour une analyse de l’historique de temps réussie, les pas de temps doivent être sélectionnés de manière « appropriée ». En fin de compte, le choix est un compromis entre temps de calcul et précision. Pour la méthode d’analyse linéaire de l’historique de temps, la recommandation suivante peut être donnée (voir [2]) :
- En tenant compte de l’accélérogramme et des diagrammes de temps transitoires, la plus courte durée de l’excitation discrète doit être divisée en au moins sept pas de temps.
- Pour un calcul du pas de temps, la fréquence la plus élevée « f » du modèle qui est pertinente pour la réponse du système devrait être utilisée comme suit : Δt ≤ 1 / (20f). De manière analogue, il convient de vérifier si la fréquence la plus élevée de l’excitation est prise en compte dans la condition Δt ≤ 𝜋 / (10ω). Dans le cas, le pas de temps doit être corrigé.
