Rejestracja Podstawowe zarządza ustawieniami dotyczącymi metody oraz krokami czasowymi.
Rodzaj metody analizy czasowej
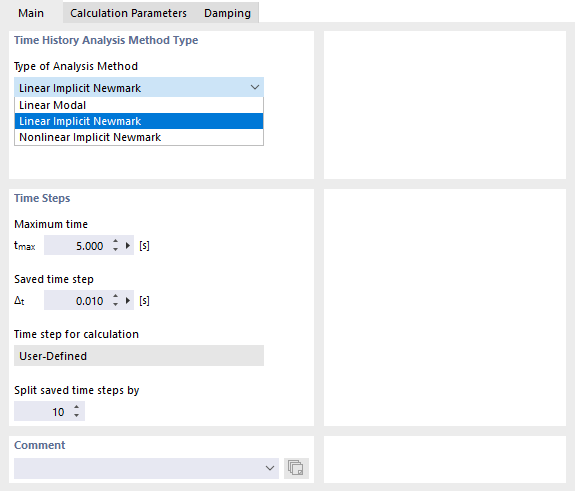
W programie RFEM na liście dostępne są dwie metody liniowe i jedna nieliniowa (zob. rysunek Określanie metody weryfikacji i kroków czasowych):
- Liniowy modalny
- Liniowa analiza implicit Newmarka
- Nieliniowa analiza implicit Newmarka
W RSTAB lista zawiera dwie metody liniowe i dwie nieliniowe:
- Liniowy modalny
- Liniowa analiza implicit Newmarka
- Nieliniowy jawny | I. rząd
- Nieliniowy jawny | III. rząd
Dwie pierwsze metody analizy są geometrycznie liniowe, co oznacza, że są ważne tylko dla małych odkształceń. Ponadto wszystkie nieliniowe cechy modelu są ignorowane (na przykład niewzięcie pod uwagę awarii podparcia) lub zastępowane (pręt naciągowy jest odwzorowywany jako pręt kratownicy).
Liniowa modalna metoda analizy wykorzystuje odseparowany układ oparty na wartościach własnych i formach własnych modelu, określony w przypisanym przypadku obciążenia analizy modalnej . Układ wielofunkcyjnym ("MDOF") zostaje rozdzielony na wiele układów jednofunkcyjnych ("SDOF") (zdiagonalizowane macierze mas i sztywności). Określona liczba wartości własnych jest wymagana, aby zapewnić dokładność. Rozwiązanie odseparowanego układu jest następnie określone za pomocą implicit solvera równań Newmarka. Ustawienia macierzy mas i zmiany sztywności są przejmowane z przypisanego przypadku obciążenia analizy modalnej. Gdy wartości własne są już określone, ta metoda analizy jest nieco szybsza niż liniowa analiza implicit Newmarka.
Liniowa analiza implicit Newmarka to bezpośrednia metoda integracji w czasie. Wymaga odpowiednio małych kroków czasowych, aby osiągnąć dokładne wyniki. Przy tej metodzie analizy nie jest wymagana analiza drgań własnych. Teoretyczne podstawy zostały omówione na przykład w [1]. Za pomocą implicit method wartości nieznane w czasie i + 1 są określane na podstawie wartości w czasie i i i + 1. Nieliniowe równania muszą być rozwiązywane; nie są wymagane kontrole iteracji ani konwergencji.
Nieliniowa analiza implicit Newmarka bierze pod uwagę geometryczne i konstrukcyjne nieliniowości modelu. Metoda ta jest bezwarunkowo stabilna: nie istnieje górna granica stabilności w kroku czasowym Δt. Aby osiągnąć dokładne wyniki, nadal konieczne są odpowiednio małe kroki czasowe. Inkrement czasowy zależy od pobudzenia, częstotliwości modelu i złożoności nieliniowości. Nie ma ograniczeń dotyczących macierzy mas ani tłumienia Rayleigha.
Nieliniowa metoda jawna w RSTAB wykorzystuje metodę centralnych różnic. Jest odpowiednia dla krótkotrwałych pobudzeń oraz szybko zmieniających się nieliniowości w modelu. Metoda jest jednoznaczna, ponieważ wartości nieznane opierają się tylko na czasie i, a nie na nieznanej odpowiedzi w czasie i + 1. Jawna zasada integracji dobrze współpracuje z diagonalną macierzą mas i ograniczeniem macierzy tłumienia C = αM. Metoda jest warunkowo stabilna: uzyskana rozwiązanie ograniczone jest jedynie, gdy krok czasowy Δt jest mniejszy niż stabilny krok czasowy Δtstabil. Limit stabilności można określić na podstawie największej wartości własnej w modelu ωmax oraz udziału krytycznego tłumienia D w największej formie własnej.
Dla praktyki stabilny krok czasowy można obliczyć za pomocą następującej oceny:
Prędkość fali dylatacyjnej można obliczyć dla materiału liniowego elastycznego (o współczynniku Poissona równym zero) za pomocą:
Ta ocena pozwala na mniejsze kroki czasowe w porównaniu do dokładnego limitu stabilności. Należy jednak zauważyć, że przy tej ocenie wiele efektów nie jest uchwyconych, a z powodu dokładności może być wymagana mniejsza jednostka czasowa Δt. Program używa stałego kroku czasowego - stabilnego kroku początkowego lub wartości zdefiniowanej przez użytkownika.
Kroki czasowe
Określ 'Maksymalny czas' tmax, który ma być analizowany w obliczeniach. Następnie w polu 'Zachowany krok czasowy' ustal, w którym przedziale Δt mają być zapisywane wyniki. Tylko dla tych kroków czasowych wyniki będą dostępne. Dynamiczna obudowa powstaje z zachowanych kroków czasowych.
Ponadto obok kroków czasowych, które mają być zapisane, należy określić kroki czasowe do rzeczywistych obliczeń. Podaj wartość w polu 'Podziel zachowane kroki czasowe przez', według której zachowane kroki czasowe Δt zostaną podzielone.
Dla pomyślnego przebiegu analizy czasowej kroki czasowe powinny być "odpowiednio" dobrane. Ostatecznie decyzja to kompromis między czasem obliczeń a dokładnością. Dla liniowego przebiegu czasowego można sformułować następujące zalecenie (zob. [2 ]):
- Z uwzględnieniem akcelerogramu i czasowych wykresów przejściowych, najkrótsza długość dyskretnego pobudzenia powinna być podzielona na co najmniej siedem kroków czasowych.
- Aby obliczyć krok czasowy, należy użyć najwyższej częstotliwości f modelu, która jest istotna dla odpowiedzi układu: Δt ≤ 1 / (20f). Analogicznie należy sprawdzić, czy największa częstotliwość pobudzenia jest objęta warunkiem Δt ≤ 𝜋 / (10ω). W przeciwnym razie krok czasowy należy skorygować.