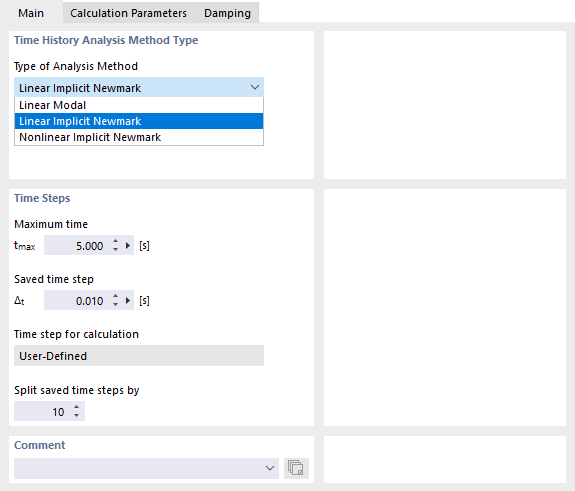
Register Základ spravuje předvolby pro metodu a časové kroky.
Typ metody analýzy časového průběhu
V programu RFEM jsou v seznamu k dispozici dvě lineární a jedna nelineární analytická metoda (viz obrázek Určení metody analýzy a časových kroků):
- Lineární modální
- Lineární implicitní Newmarkova analýza
- Nelineární implicitní Newmarkova analýza
V RSTAB seznam obsahuje dvě lineární a dvě nelineární analytické metody:
- Lineární modální
- Lineární implicitní Newmarkova analýza
- Nelineární explicitní | 1. řád
- Nelineární explicitní | 3. řád
První dvě analytické metody v obou programech jsou geometricky lineární, což znamená, že jsou platné pouze pro malé deformace. Dále jsou všechny nelineární vlastnosti modelu ignorovány (například není zohledněno selhání podpory) nebo jsou nahrazeny (tahová výztuž je modelována jako prut).
Lineární modální analytická metoda používá oddělený systém založený na vlastních hodnotách a vlastních tvarech modelu, který je určen ve přiřazeném lastovém případu modální analýzy . Systém s více stupni volnosti ("MDOF") je rozložen na několik systémů s jedním stupněm volnosti ("SDOF") (diagonalizovaná matice hmot a tuhosti). K zajištění přesnosti je potřebný určitý počet vlastních hodnot. Řešení odděleného systému je následně určeno pomocí implicitního Newmarkova řešiče rovnic. Nastavení matice hmot a změny tuhosti jsou převzaty z přiřazeného modálního lastového případu. Pokud jsou vlastní hodnoty již určeny, je tato analytická metoda o něco rychlejší než lineární implicitní Newmarkova analýza.
Lineární implicitní Newmarkova analýza je přímá časově integrační metoda. K dosažení přesných výsledků vyžaduje dostatečně malé časové kroky. U této analytické metody není vyžadována analýza vlastních kmitů. Teoretický základ je například vysvětlen v [1]. Pomocí implicitních řešičů jsou neznámé hodnoty času i + 1 určovány na základě hodnot času i a i + 1. Je třeba řešit nelineární rovnice; nejsou vyžadovány žádné iterace a ověřování konvergence.
Nelineární implicitní Newmarkova analýza zohledňuje geometrické a konstrukční nelinearity modelu. Tato metoda je bezpodmínečně stabilní: Neexistuje žádná horní hranice stability v časovém kroku Δt. Přesto jsou pro přesné výsledky potřebné dostatečně malé časové kroky. Časový interval závisí na excitaci, kmitočtu modelu a složitosti nelinearit. Neexistují žádná omezení týkající se matice hmot a Rayleighova tlumení.
Nelineární explicitní metoda v RSTAB využívá metodu centrálních rozdílů. Je vhodná pro krátkodobé excitace a rychle se měnící nelinearity v modelu. Metoda je jednoznačná, protože neznámé hodnoty jsou založeny pouze na čase i a ne na neznámé odpovědi v čase i + 1. Explicitní integrační pravidlo funguje dobře v kombinaci s diagonální maticí hmot a s omezením matice tlumení C = αM. Metoda je podmíněně stabilní: Omezené řešení je dosaženo, pouze pokud je časový interval Δt menší než stabilní časový interval Δtstabil. Hranice stability může být definována z největší vlastní hodnoty modelu ωmax a podílu kritického tlumení D na největším vlastním tvaru.
Pro praktickou aplikaci může být stabilní časový krok odhadnut pomocí následující hodnoty:
Rychlost dilatačních vln se pro lineárně elastický materiál (s Poissonovým poměrem rovno nule) určuje z:
Tento odhad umožňuje menší časové kroky ve srovnání s přesným limitem stability. Tento odhad však musí zvážit, že mnoho efektů není zachyceno a kvůli přesnosti může být požadován menší časový krok Δt. Program používá pevnou šířku časového kroku – buď stabilní počáteční časový interval, nebo uživatelsky definovanou hodnotu.
Časové kroky
Zadejte 'Maximální čas' tmax, který má být během výpočtu zkoumán. Poté určete v poli 'Uložený časový krok', v jakém intervalu Δt mají být jednotlivé výsledky uloženy. Pouze pro tyto časové kroky budou k dispozici výsledky. I dynamický obálka je tvořena z uložených časových kroků.
Kromě uložených časových kroků musí být stanoveny časové kroky pro samotný výpočet. Zadejte hodnotu do pole 'Uložené časové kroky dělené' hodnotou, kterou mají být uložené časové kroky Δt děleny.
Pro úspěšný časově závislý postup by měly být časové kroky "přiměřeně" zvoleny. Konečné rozhodnutí je kompromis mezi časem výpočtu a přesností. Pro lineární časově závislou metodu lze doporučit následující (viz [2]):
- Při zohlednění akcelerogramu a přechodových časových diagramů by měla být nejkratší délka diskrétní excitace rozdělena na nejméně sedm časových kroků.
- Při výpočtu časového kroku by měl být použit nejvyšší kmitočet f modelu, který je relevantní pro odezvu systému, následujícím způsobem: Δt ≤ 1 / (20f). Analogicky by mělo být zkontrolováno, zda je největší frekvence excitace zachycena v podmínce Δt ≤ 𝜋 / (10ω). Pokud tomu tak není, měl by být časový krok upraven.