Basis

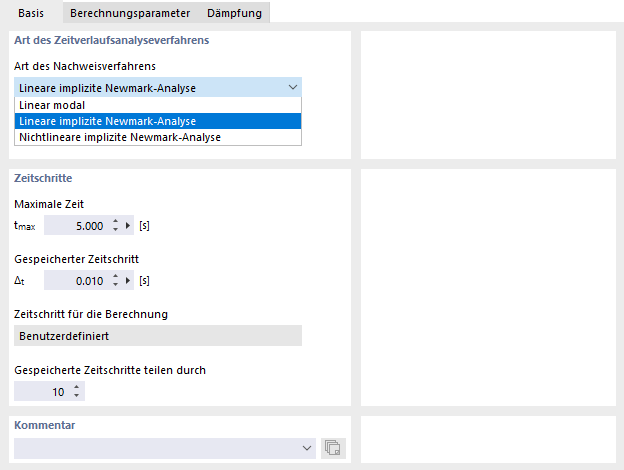
Das Register Basis verwaltet die Vorgaben für das Verfahren und die Zeitschritte.

Nachweisverfahren und Zeitschritte festlegen

Art des Zeitverlaufsanalyseverfahrens

Im Programm RFEM stehen in der Liste zwei lineare und ein nichtlineares Analyseverfahren zur Auswahl (siehe Bild Nachweisverfahren und Zeitschritte festlegen):

• Linear modal
• Lineare implizite Newmark-Analyse
• Nichtlineare implizite Newmark-Analyse

In RSTAB enthält die Liste zwei lineare und zwei nichtlineare Analyseverfahren:

• Linear modal
• Lineare implizite Newmark-Analyse
• Nichtlinear explizit | I. Ordnung
• Nichtlinear explizit | III. Ordnung

Die jeweils ersten beiden Analyseverfahren sind geometrisch linear, sodass sie nur für kleine Verformungen gültig sind. Ferner werden alle nichtlinearen Eigenschaften des Modell entweder ignoriert (beispielsweise wird der Ausfall eines Lagers nicht berücksichtigt) oder ersetzt (ein Zugstab wird durch einen Fachwerkstab abgebildet).

Das linear modale Analyseverfahren verwendet ein entkoppeltes System, das auf den Eigenwerten und Eigenformen des Modells basiert und im zugewiesenen Modalanalyse-Lastfall bestimmt wird. Das Mehrfreiheitsgradsystem ("MDOF") wird in viele Einfreiheitsgradsysteme ("SDOF") zerlegt (diagonalisierte Massen- und Steifigkeitsmatrix). Eine gewisse Anzahl an Eigenwerten ist erforderlich, damit die Genauigkeit gewährleistet ist. Die Lösung des entkoppelten Systems wird anschließend mit einem impliziten Newmark-Gleichungslöser bestimmt. Die Einstellungen der Massenmatrix und die Steifigkeitsänderungen werden vom zugewiesenen Modalanalyse-Lastfall übernommen. Wenn die Eigenwerte bereits bestimmt sind, ist dieses Analyseverfahren etwas schneller als die lineare implizite Newmark-Analyse.

Die lineare implizite Newmark-Analyse ist ein direktes Zeit-Integrationsverfahren. Es benötigt ausreichend kleine Zeitschritte, um exakte Ergebnisse zu erzielen. Bei diesem Analyseverfahren ist keine Eigenschwingungsanalyse erforderlich. Der theoretische Hintergrund ist beispielsweise in [1] erläutert. Mit impliziten Lösungsverfahren werden unbekannte Werte der Zeit i + 1 auf der Grundlage der Werte der Zeit i und i + 1 ermittelt. Dabei müssen nichtlineare Gleichungen gelöst werden; es sind keine Iterations- und Konvergenzkontrollen erforderlich.

Die nichtlineare implizite Newmark-Analyse berücksichtigt geometrische und konstruktive Nichtlinearitäten des Modells. Das Verfahren ist unbedingt stabil: Es gibt keine obere Stabilitätsgrenze im Zeitschritt Δt. Für exakte Ergebnisse sind dennoch ausreichend kleine Zeitschritte nötig. Das Zeitinkrement ist abhängig von der Erregung, der Frequenz des Modells und der Komplexität der Nichtlinearitäten. Es gibt keine Einschränkungen hinsichtlich der Massenmatrix und der Rayleigh-Dämpfung.

Das nichtlinear explizite Verfahren von RSTAB nutzt die Methode der zentralen Differenzen. Es eignet sich für Erregungen von kurzer Dauer und sich rasch ändernde Nichtlinearitäten im Modell. Die Methode ist eindeutig, weil unbekannte Werte nur auf der Zeit i basieren und nicht auf der unbekannten Antwort zur Zeit i + 1. Die explizite Integrationsregel funktioniert gut in Kombination mit einer diagonalen Massenmatrix und mit der Beschränkung der Dämpfungsmatrix C = αM. Die Methode ist bedingt stabil: Eine begrenzte Lösung wird nur erreicht, wenn das Zeitinkrement Δt kleiner als das stabile Zeitinkrement Δt_stabil ist. Das Stabilitätslimit kann aus dem größten Eigenwert im Modell ω_max und dem Anteil der kritischen Dämpfung D an der größten Eigenform definiert werden.

Für die Praxis kann das stabile Zeitinkrement mit folgendem Schätzwert ermittelt werden:

Die Dilatationswellen-Geschwindigkeit ermittelt sich für ein linear elastisches Material (mit der Querdehnzahl gleich null) aus:

Dieser Schätzwert erlaubt kleinere Zeitschritte im Vergleich zum exakten Stabilitätslimit. Bei dieser Schätzung ist jedoch zu beachten, dass viele Effekte nicht erfasst sind und auch aufgrund der Genauigkeit ein kleinerer Zeitschritt Δt erforderlich sein kann. Das Programm verwendet eine feste Zeitschrittweite – das stabile Anfangs-Zeitinkrement oder einen benutzerdefinierten Wert.

Zeitschritte

Geben Sie die 'Maximale Zeit' t_max an, die bei der Berechnung untersucht werden soll. Legen Sie dann im Feld 'Gespeicherter Zeitschritt' fest, in welchem Intervall Δ_t jeweils Ergebnisse abgelegt werden sollen. Nur für diese Zeitschritte werden Ergebnisse verfügbar sein. Auch die dynamische Umhüllende wird aus den gespeicherten Zeitschritten gebildet.

Zusätzlich zu den Zeitschritten, die gespeichert werden, sind Zeitschritte für die eigentliche Berechnung festzulegen. Geben Sie hierzu im Feld 'Gespeicherte Zeitschritte teilen durch' einen Wert an, durch den die gespeicherten Zeitschritte Δ_t geteilt werden sollen.

Für ein erfolgreiches Zeitverlaufsverfahren sollten die Zeitschritte "angemessen" gewählt werden. Letztendlich ist die Entscheidung ein Kompromiss zwischen Berechnungszeit und Genauigkeit. Für das lineare Zeitverlaufsverfahren kann folgende Empfehlung ausgesprochen werden (siehe [2]):

• Unter Berücksichtigung des Akzelerogramms und der transienten Zeitdiagramme sollte die kürzeste Länge der diskreten Erregung in mindestens sieben Zeitschritte unterteilt werden.
• Für die Berechnung des Zeitschritts sollte die höchste Frequenz f des Modells, die für die Systemantwort relevant ist, wie folgt verwendet werden: Δt ≤ 1 / (20f). Analog sollte überprüft werden, ob die größte Frequenz der Erregung in der Bedingung Δt ≤ 𝜋 / (10ω) erfasst ist. Ist dies nicht der Fall, sollte der Zeitschritt korrigiert werden.