Base

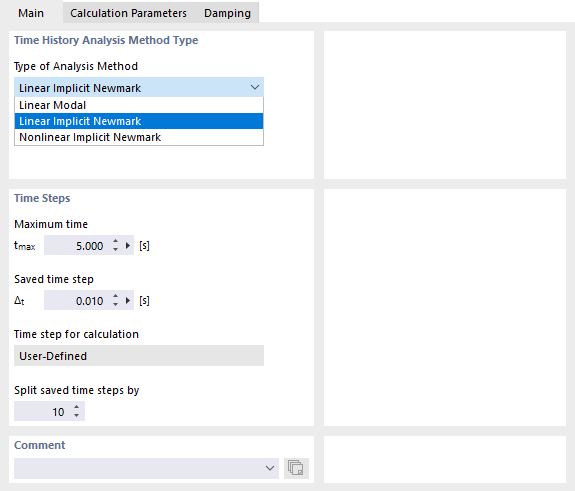
Il registro Base gestisce le impostazioni predefinite per il metodo e i passaggi temporali.

@image044494@

Impostazione del metodo di verifica e dell’intervallo di tempo

@analysis-method@

Tipo di metodo di analisi dinamica

Nel programma RFEM, nell'elenco sono disponibili due metodi di analisi lineari e uno non lineare (vedere l'immagine Impostare il metodo di verifica e i passaggi di tempo):

• Lineare modale
• Analisi di Newmark implicita lineare
• Analisi di Newmark implicita non lineare

In RSTAB, l'elenco contiene due metodi di analisi lineari e due non lineari:

• Lineare modale
• Analisi di Newmark implicita lineare
• Non lineare esplicito | I ordine
• Non lineare esplicito | III ordine

I primi due metodi di analisi sono geometricamente lineari, quindi sono validi solo per piccoli spostamenti. Inoltre, tutte le proprietà non lineari del modello vengono ignorate (ad esempio, il collasso di un supporto non viene considerato) o sostituite (una tirante viene rappresentata da un'asta reticolata).

Il metodo di analisi lineare modale utilizza un sistema disaccoppiato basato sui valori e le forme caratteristiche del modello determinati nel caso di carico di analisi modale assegnato. Il sistema a più gradi di libertà ("MDOF") viene suddiviso in tanti sistemi a un grado di libertà ("SDOF") (matrice di massa e di rigidezza diagonalizzate). È necessario un certo numero di valori caratteristici per garantire l'accuratezza. La soluzione del sistema disaccoppiato viene quindi determinata tramite un risolutore delle equazioni di Newmark implicito. Le impostazioni della matrice di massa e le variazioni di rigidezza vengono ereditate dal caso di carico di analisi modale assegnato. Se i valori caratteristici sono già stati determinati, questo metodo di analisi è leggermente più veloce rispetto all'analisi di Newmark implicita lineare.

Lanalisi di Newmark implicita lineare è un metodo di integrazione diretto nel tempo. Richiede passi temporali sufficientemente piccoli per ottenere risultati accurati. In questo metodo di analisi non è richiesta un'analisi delle vibrazioni proprie. Il contesto teorico è spiegato, ad esempio, in [1]. Nei metodi di soluzione impliciti, i valori incogniti al tempo i + 1 sono determinati sulla base dei valori ai tempi i e i + 1. È necessario risolvere equazioni non lineari; non sono richieste iterazioni e controlli di convergenza.

Lanalisi di Newmark implicita non lineare considera le non linearità geometriche e costruttive del modello. Il metodo è assolutamente stabile: non c'è un limite superiore di stabilità nel passo di tempo Δt. Tuttavia, per ottenere risultati accurati, sono necessari passi temporali sufficientemente piccoli. L'incremento di tempo dipende dall'eccitazione, dalla frequenza del modello e dalla complessità delle non linearità. Non ci sono restrizioni sulla matrice di massa e sullo smorzamento di Rayleigh.

Il metodo non lineare esplicito di RSTAB utilizza il metodo delle differenze centrali. È adatto per eccitazioni di breve durata e non linearità che cambiano rapidamente nel modello. Il metodo è chiaro perché i valori sconosciuti si basano solo sul tempo i e non sulla risposta incognita al tempo i + 1. La regola di integrazione esplicita funziona bene in combinazione con una matrice di massa diagonale e con la limitazione della matrice di smorzamento C = αM. Il metodo è condizionalmente stabile: viene raggiunta una soluzione finita solo se l'incremento di tempo Δt è inferiore all'incremento di tempo stabile Δt_stabile. Il limite di stabilità può essere definito dal valore caratteristico più grande nel modello ω_max e dalla percentuale di smorzamento critico D sulla forma caratteristica più grande.

@formula002140@

In pratica, l'incremento di tempo stabile può essere determinato con la seguente stima:

La velocità dell'onda di dilatazione, per un materiale elastico lineare (con la ratio di Poisson pari a zero), si determina secondo:

Questo valore stimato comporta passi di tempo più piccoli rispetto al Limite di stabilità esatto. Tuttavia, è importante notare che molti effetti non sono considerati in questa stima e un passo temporale più piccolo Δt può essere necessario per motivi di precisione. Il programma utilizza una larghezza di passo temporale fissa - l'incremento di tempo iniziale stabile o un valore definito dall'utente.

@time-steps@

Passaggi temporali

Indicare il 'Tempo massimo' t_max che deve essere esaminato nel calcolo. Quindi, specificare nel campo 'Passo temporale memorizzato' in quale intervallo Δ_t devono essere salvati i risultati. Solo per questi passi temporali saranno disponibili i risultati. Anche l'involucro dinamico viene costituito dai passi temporali salvati.

È necessario impostare passi temporali per il calcolo effettivo oltre a quelli che devono essere salvati. A tale scopo, inserire un valore nel campo 'Dividere i passi temporali memorizzati per' che divida i passi temporali salvati Δ_t.

Per un'analisi dinamica efficace, i passi temporali devono essere scelti "in modo appropriato". Alla fine, la decisione è un compromesso tra tempo di calcolo e accuratezza. Per il procedimento dinamico lineare, si possono fare le seguenti raccomandazioni (vedere [2]):

• Considerando l'accelerogramma e i diagrammi temporali transitori, la durata più breve dell'eccitazione discreta dovrebbe essere suddivisa in almeno sette passi temporali.
• Per il calcolo del passo temporale, la frequenza più elevata f del modello rilevante per la risposta del sistema dovrebbe essere utilizzata come segue: Δt ≤ 1 / (20f). Analogamente, dovrebbe essere verificato se la frequenza più alta dell'eccitazione è catturata nella condizione Δt ≤ 𝜋 / (10ω). Se non lo è, il passo temporale dovrebbe essere corretto.