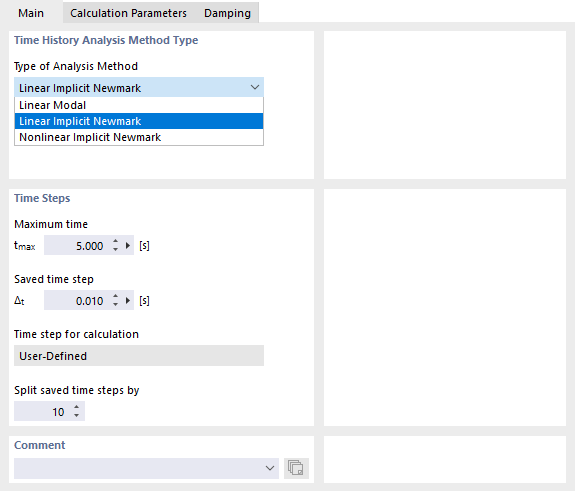
El registro Base gestiona las configuraciones para el método y los pasos de tiempo.
Tipo de método de análisis de historial de tiempo
En el programa RFEM, hay disponibles dos métodos de análisis lineales y uno no lineal para seleccionar en la lista (ver imagen Establecer criterios y pasos de tiempo):
- Modal lineal
- Análisis implícito de Newmark lineal
- Análisis implícito de Newmark no lineal
En RSTAB, la lista contiene dos métodos de análisis lineales y dos no lineales:
- Modal lineal
- Análisis implícito de Newmark lineal
- No lineal explícito | Primer orden
- No lineal explícito | Tercer orden
Los dos primeros métodos de análisis son geométricamente lineales, por lo que son válidos solo para pequeñas deformaciones. Además, todas las propiedades no lineales del modelo son ignoradas (por ejemplo, no se considera la falla de un soporte) o reemplazadas (una barra de tracción se representa mediante un elemento de celosía).
El método de análisis modal lineal utiliza un sistema desacoplado basado en los valores y formas propias del modelo, determinados en el caso de carga de análisis modal asignado. El sistema de múltiples grados de libertad ("MDOF") se descompone en varios sistemas de un solo grado de libertad ("SDOF") (matriz de masa y rigidez diagonalizada). Se requiere una cierta cantidad de valores propios para garantizar la precisión. La solución del sistema desacoplado se determina luego con un solucionador de ecuaciones implícito de Newmark. Los ajustes de la matriz de masa y los cambios de rigidez se toman del caso de carga de análisis modal asignado. Si los valores propios ya están determinados, este método de análisis es algo más rápido que el análisis implícito de Newmark lineal.
El análisis implícito de Newmark lineal es un método de integración temporal directa. Requiere pasos de tiempo suficientemente pequeños para obtener resultados precisos. Este método de análisis no requiere un análisis de vibraciones naturales. El fondo teórico se describe, por ejemplo, en [1]. Con métodos de solución implícitos, se determinan valores desconocidos en el tiempo i + 1 en base a los valores en el tiempo i e i + 1. No es necesario resolver ecuaciones no lineales, ni se requieren controles de iteración y convergencia.
El análisis implícito de Newmark no lineal considera las no linealidades geométricas y estructurales del modelo. El método es incondicionalmente estable: no hay límite superior de estabilidad en el paso de tiempo Δt. Sin embargo, se requieren pasos de tiempo suficientemente pequeños para obtener resultados precisos. El incremento de tiempo depende de la excitación, la frecuencia del modelo y la complejidad de las no linealidades. No hay restricciones con respecto a la matriz de masa y la amortiguación de Rayleigh.
El método no lineal explícito de RSTAB utiliza el método de diferencias centrales. Es adecuado para excitaciones de corta duración y no linealidades que cambian rápidamente en el modelo. El método es explícito porque los valores desconocidos se basan solo en el tiempo i y no en la respuesta desconocida en el tiempo i + 1. La regla de integración explícita funciona bien en combinación con una matriz de masas diagonal y con la restricción de la matriz de amortiguación C = αM. El método es condicionalmente estable: solo se logra una solución limitada si el incremento de tiempo Δt es menor que el incremento de tiempo estable Δtestable. El límite de estabilidad puede ser definido a partir del mayor valor propio en el modelo ωmax y la proporción de amortiguamiento crítico D en la forma propia más grande.
Para la práctica, el incremento de tiempo estable puede determinarse con la siguiente estimación:
La velocidad de las ondas de dilatación se determina para un material lineal elástico (con el coeficiente de Poisson igual a cero) como:
Esta estimación permite pasos de tiempo más pequeños en comparación con el límite de estabilidad exacto. Sin embargo, debe tenerse en cuenta que en esta estimación no se consideran muchos efectos y que puede requerirse un paso de tiempo más pequeño Δt por razones de precisión. El programa utiliza un paso de tiempo fijo: el incremento de tiempo inicial estable o un valor definido por el usuario.
Pasos de tiempo
Indique el 'Tiempo máximo' tmax que se examinará durante el cálculo. Luego, establezca en el campo 'Paso de tiempo guardado' el intervalo Δt en el que se almacenarán los resultados. Solo estarán disponibles resultados para estos pasos de tiempo. La envolvente dinámica también se define a partir de los pasos de tiempo guardados.
Además de los pasos de tiempo que se guardan, se deben definir pasos de tiempo para el cálculo real. Para ello, introduzca en el campo 'Dividir pasos de tiempo guardados por' un valor por el que se dividirán los pasos de tiempo guardados Δt.
Para que un procedimiento de historial de tiempo tenga éxito, los pasos de tiempo deben ser "adecuados". En última instancia, la decisión es un compromiso entre el tiempo de cálculo y la precisión. Para el procedimiento de historial de tiempo lineal, se puede dar la siguiente recomendación (ver [2]):
- Considerando el acelerograma y los diagramas de tiempo transitorios, la longitud más corta de la excitación discreta debe dividirse en al menos siete pasos de tiempo.
- Para el cálculo del paso de tiempo, la frecuencia más alta f del modelo relevante para la respuesta del sistema se debe utilizar de la siguiente manera: Δt ≤ 1 / (20f). También debe verificarse si la mayor frecuencia de excitación se cubre con la condición Δt ≤ 𝜋 / (10ω). Si no es así, se debe corregir el paso de tiempo.